1、简介

弹性力学求解弹性体应力、应变、位移未知函数的时候,根据平衡微分方程、几何方程、物理方程、应力和位移边界条件,建立微分方程组。通过前人的努力,我们已经能够求解某些载荷情况下的精确解。然而对于工程应用中的复杂情况,其微分方程还是太复杂,难以求解。
于是,弹性力学产生了三种近似数值解法:变分法、差分法、有限元单元法。
弹性力学简化三大方程(平衡微分方程、几何方程、弹性方程)时,面对位移、应力、应变三大未知函数,会将其中两组函数用剩下一组函数表示。常用的是用位移表示和用应力表示。有限元采用的是前者(位移法)。
有限元素法涉及到的知识:弹性力学、结构力学、线性代数、高等数学
2、原理
基本思想:有限元,故名思义。弹性体划分为有限单元。对每个小单元以近似的处理。以简单的函数近似代替复杂函数。简化运算。
3、步骤
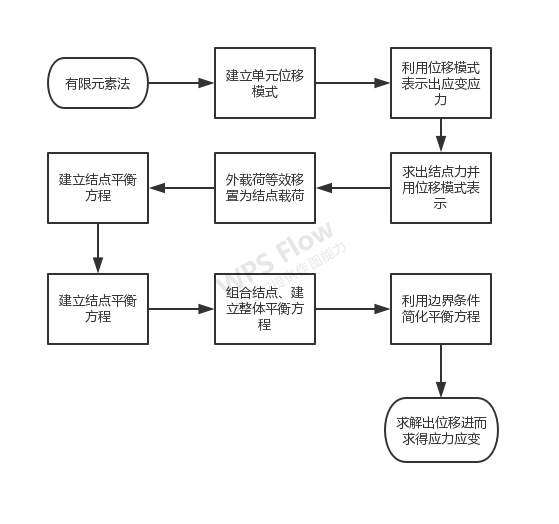
3.1 划分单元:
为什么要将一个完整的弹性体划分为有限的多个单元。你可以类比学微积分的时候,为了求得函数的积分(面积)将x划分为很小的有限个小矩形。矩形的面积好算,就用矩形的面积近似整个积分。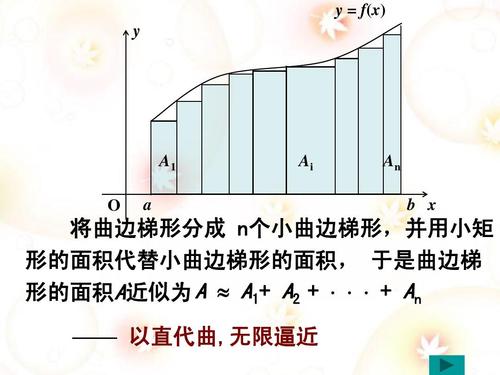

3.2. 建立位移模式:
在弹性力学中我们会遇到以坐标为自变量的位移函数。这些函数很复杂。可我们有一个好的拟合工具—泰勒级数,将复杂的函数用多项式表示。当然我们不会取无限项,所以取有限项近似表示。值得注意的是,泰勒级数往往在接近已知函数值附近才比较精确。所以我们将弹性体划分为有限个单元,每个单元用各自的泰勒级数表征自己的位移函数。

需要注意的是:泰勒级数的每一项的系数并没有采用取函数的导数的方法。而是用待定系数法将单元上的结点的位移值代入到函数中求得每一个参数。(插值法)以此求得用结点表示的各个单元的位移函数,即位移模式。
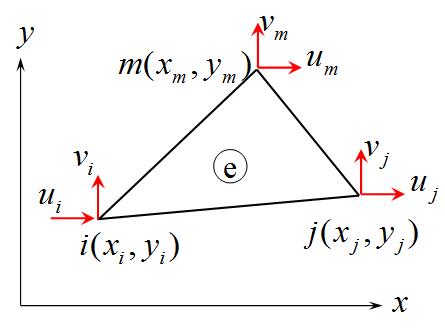
将三角形单元中的位移函数表示如下形式:
\[u=\alpha_1 + \alpha_2 x + \alpha_3 y , v=\alpha_4 + \alpha_5 x + \alpha_6 y \tag{1}\]
其中 \( \alpha_1、\alpha_2、\alpha_3 \) 是待定参数
代入i,j,m三个结点:
\[\alpha_1 + \alpha_2 x_i +\alpha_3 y_i = u_i , \alpha_4 + \alpha_5 x_i +\alpha_6 y_i = v_i\]
\[\alpha_1 + \alpha_2 x_j +\alpha_3 y_j = u_j , \alpha_4 + \alpha_5 x_j +\alpha_6 y_j = v_j\]
\[\alpha_1 + \alpha_2 x_m +\alpha_3 y_m = u_m, \alpha_4 + \alpha_5 x_m +\alpha_6 y_m = v_m\]
利用以上方程可以解出系数 \( \alpha_1 、\alpha_2、\alpha_3、\alpha_4、\alpha_5、\alpha_6 \) ,代回 \( (1) \) 中,经过整理,可以写成:
\[\left.\begin{matrix} u = N_i u_i + N_j u_j + N_m u_m\\ v = N_i v_i + N_j v_j + N_m v_m\end{matrix}\right\}\tag{2}\]
其中:
\[N_i = \frac{ \begin{vmatrix} {1}&{x}&{y}\\ {1}&{x_j}&{y_j}\\ {1}&{x_m}&{y_m}\\ \end{vmatrix}}{ \begin{vmatrix} {1}&{x_i}&{y_i}\\ {1}&{x_j}&{y_j}\\ {1}&{x_m}&{y_m}\\ \end{vmatrix}},(i,j,m轮换)\]
上式也可以改写为:
\[N_i = (a_i + b_i x + c_i y) / 2A ,(i,j,m轮换)\]
其中:
\[a_i = \begin{vmatrix} {x_j}&{y_j}\\ {x_m}&{y_m}\end{vmatrix},b_i = -\begin{vmatrix} {1}&{y_j}\\ {1}&{y_m}\end{vmatrix},c_i = \begin{vmatrix} {1}&{x_j}\\ {1}&{x_m}\end{vmatrix},A = \frac{1}{2}\begin{vmatrix} {1}&{x_i}&{y_i}\\ {1}&{x_j}&{y_j}\\ {1}&{x_m}&{y_m}\end{vmatrix}(三角形ijm面积)\]
用矩阵表示上述关系:
\[{\bf d} = {\bf N}{\bf \delta^e}\]
其中:
\[{\bf d} =\begin{pmatrix} u&v\end{pmatrix}^T,{\bf \delta ^e} = \begin{pmatrix} {\bf \delta_i}&{{\bf \delta_j}}&{\bf \delta_m}\end{pmatrix}^T,\]
\[{\bf N} = \begin{pmatrix} N_i&0&N_j&0&N_m&0\\ 0&N_i&0&N_j&0&N_m\end{pmatrix}\]
N称为形函数矩阵
3.3 利用位移模式表示出应力应变:
这步是将位移模式代入几何方程和物理方程,用位移模式表示单元应力和应变。
将几何方程写作矩阵形式:
\[{\bf \epsilon} = \begin{pmatrix} \epsilon_x\\ \epsilon_y\\ \gamma_{xy}\end{pmatrix} =\begin{pmatrix} \frac{\partial u}{\partial x}\\ \frac{\partial v}{\partial y}\\ \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\end{pmatrix}\]
代入 \( (2) \) 式
\[{\bf \epsilon} = \frac{1}{2A}\begin{pmatrix} b_i&0&b_j&0&b_m&0\\ 0&c_i&0&c_j&0&c_m\\ c_i&b_i&c_j&b_j&c_m&b_m\\\end{pmatrix} \begin{pmatrix} u_i\\ v_i\\ u_j\\ v_j\\ u_m\\ v_m\end{pmatrix}\]
简写为:
\[{\bf \epsilon = B\delta^e} \tag{3}\]
至此已将应变表示为位移模式。接下来代入物理方程将应力表示为位移模式:
将物理方程写作矩阵形式:
\[{\bf \sigma} = \begin{pmatrix} \sigma_x\\ \sigma_y\\ \tau_{xy}\end{pmatrix} = \frac{E}{1-\mu^2}\begin{pmatrix} 1&\mu&0\\ \mu&1&0\\ 0&0&\frac{1-\mu}{2}\end{pmatrix}\begin{pmatrix} \epsilon_x\\ \epsilon_y\\ \gamma_{xy}\end{pmatrix}\]
简写为:
\[{\bf \sigma = D \epsilon} \tag{4}\]
其中:
\[{\bf D} = \frac{E}{1-\mu^2}\begin{pmatrix} 1&\mu&0\\ \mu&1&0\\ 0&0&\frac{1-\mu}{2}\end{pmatrix}\]
将 \( (4) \) 代入 \( (3) \) 中:
\[{\bf \sigma = DB\delta^e = S\delta^e} \tag{5}\]
其中 \( {\bf S = DB} \) 为应力变换矩阵
3.4 求出结点力并用位移模式表示:
现在将每个单元的结点和单元内部拆分开。由牛顿第三定律,结点对单元的力(结点力 \( {\bf F^e} \) )大小等于单元对结点的力( \( {\bf -F^e} \) )的大小。于是我们现在利用虚功原理求出结点对单元的力。
注意:由于单元对结点的力和结点对单元的力等大反向,在不至于混淆的情况下,现在将二者统称为结点力。
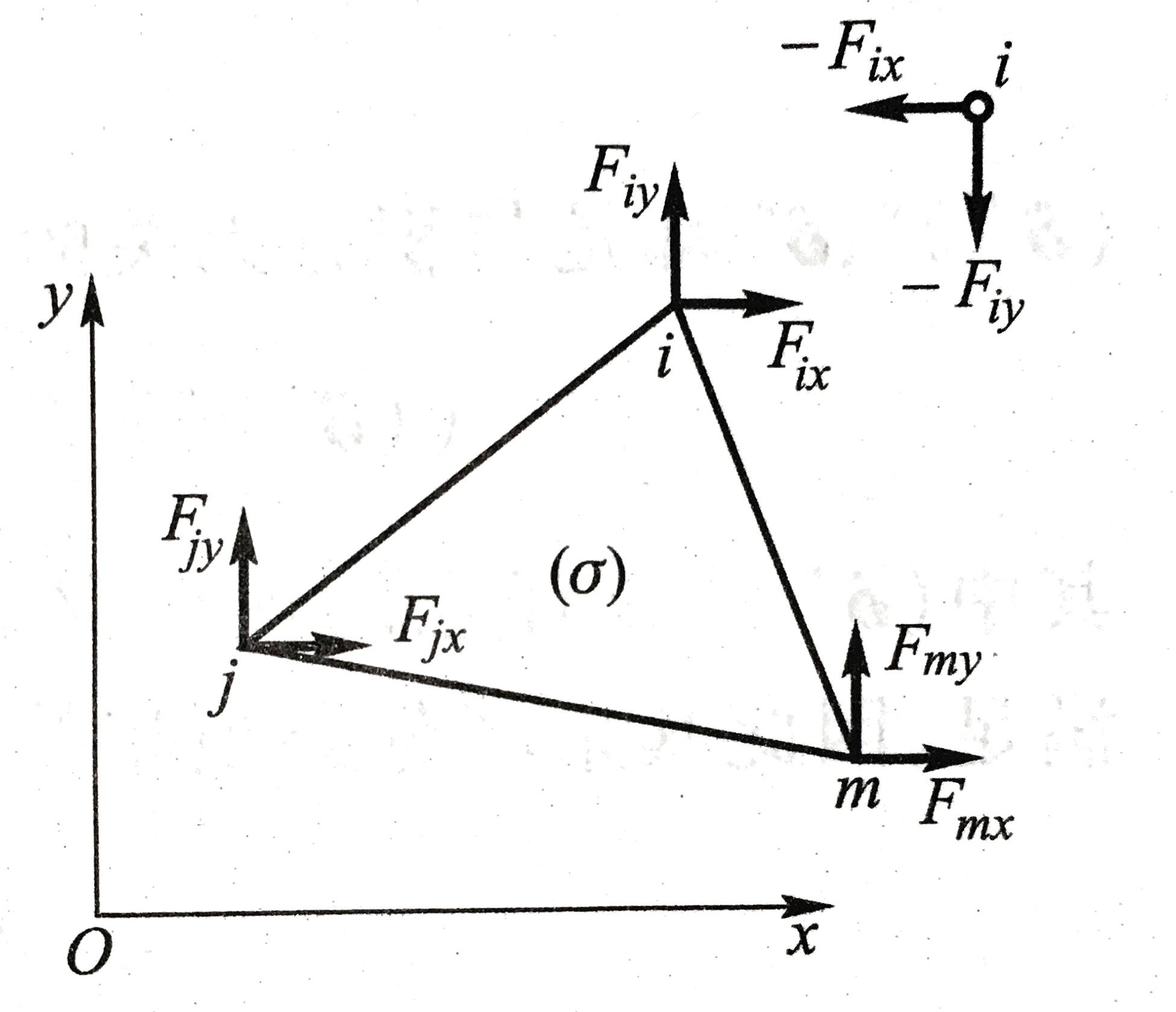
注意:作用于单元上的外载荷会通过第5步将其等效移置到结点上,故外载荷在单元内没有虚功。
结点力为:
\[{\bf F^e} = \begin{pmatrix} {\bf F_i}&{\bf F_j}&{\bf F_m}\end{pmatrix}^T = \begin{pmatrix} F_{ix}&F_{iy}&F_{jx}&F_{jy}&F_{mx}&F_{my}\end{pmatrix}^T\]
结点虚位移为:
\[{\bf (\delta^*)^e} = \begin{pmatrix} \delta^*_i&\delta^*_j&\delta^*_m\end{pmatrix}^T = \begin{pmatrix} u^*_i&v^*_i&u^*_j&v^*_j&u^*_m&v^*_m\end{pmatrix}^T\]
由位移模式得,单元内任意一点的虚位移为:
\[{\bf d^* = N(\delta^*)^e} \tag{6}\]
虚应变为:
\[{\bf \epsilon^* = B(\delta^*)^e}\]
变形体的虚功原理:一个处于平衡的构件,其外力和内力在该位置任意给定的虚位移上所作的虚功之和等于零。
由虚功原理得,在单元ijm中,外力(结点力 \( {\bf -F^e} \) )在虚位移(结点虚位移 \( {\bf (\delta ^*)^e} \) )上的虚功与应力在虚位变上的虚功之和等于零。即
\[(({\bf \delta}^*)^e)^T{\bf F}^e = \iint_A ({\bf \epsilon}^*)^T{\bf \sigma}\,{\rm d}x{\rm d}yt\]
其中, \( {\bf (\epsilon^*)^T = (B(\delta^*)^e)^T = ((\delta^*)^e)^TB^T} \) ,代入 \( (5) \) 得:
\[(({\bf \delta}^*)^e)^T{\bf F}^e = \iint_A (({\bf \delta}^*)^e)^T{\bf B}^T{\bf D}{\bf B}{\bf \delta}^e\,{\rm d}x{\rm d}yt\]
\( ({\bf \delta}^*)^e \) 和 \( {\bf \delta^e} \) 都是与积分无关的数值,从而得到:
\[(({\bf \delta}^*)^e)^T{\bf F}^e = (({\bf \delta}^*)^e)^T \iint_A {\bf B}^T{\bf D}{\bf B}\,{\rm d}x{\rm d}yt {\bf \delta}^e\]
其中 \( ({\bf \delta}^*)^e \) 是任意虚位移,因此其余部分必须相等:
\[{\bf F}^e = \iint_A {\bf B}^T{\bf D}{\bf B}\,{\rm d}x{\rm d}yt {\bf \delta}^e\]
令
\[{\bf k} = \iint_A {\bf B}^T{\bf D}{\bf B}\,{\rm d}x{\rm d}yt\]
则
\[{\bf F^e = k\delta^e} \tag{7}\]
\( {\bf k} \) 称为单元的劲度矩阵(刚度矩阵)。对于三角形单元和广义胡克定律, \( {\bf B} \) 和 \( {\bf D} \) 内都是常数,而 \( \iint_A {\rm d}x{\rm d}y = A \) ,因此
\[{\bf k} = {\bf B}^T{\bf D}{\bf B}tA\]
通过以上运算就可以把结点力用位移模式表示。
3.5 外载荷等效移置为结点载荷:
外载荷(集中力、体力、面力)会作用于单元上。有限元素法按照变形体静力等效原则,将原外载荷等效于结点上的等效外载荷(结点载荷)。
变形体静力等效原则——在任意的虚位移上,使原载荷与移置载荷的虚功相等。
3.5.1 集中力移置
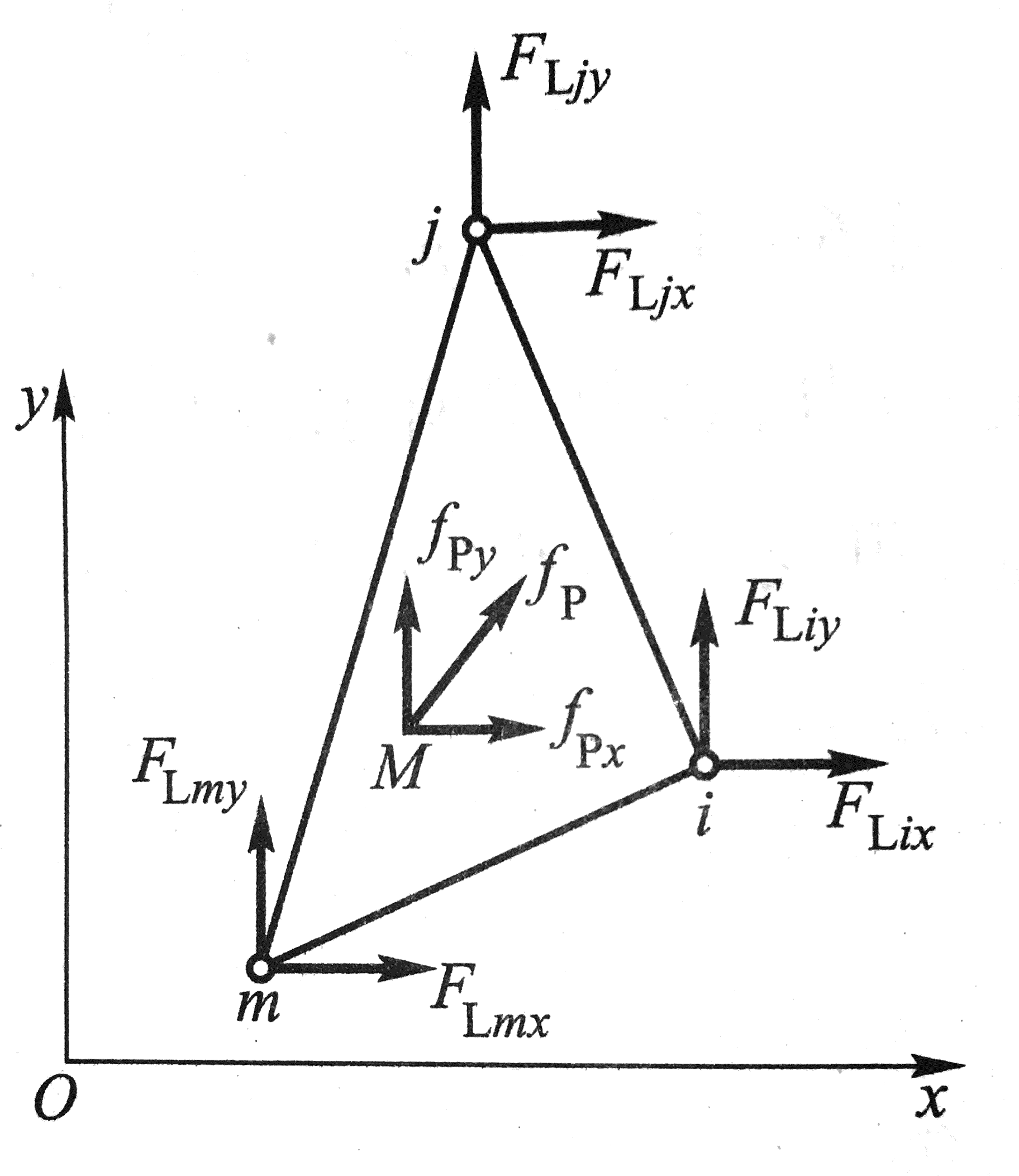
设单元ijm中坐标为(x,y)的任意一点M,在单位厚度上收有集中载荷 \( {\bf f_p} \) ,用矩阵表示为 \( {\bf f_p} = \begin{pmatrix} f_{px}&f_{py} \end{pmatrix}^T \) 。将此集中力按弹性体静力等效原则移置到结点处,转换为结点载荷,表示为:
\[{\bf F^e_L} = \begin{pmatrix} {\bf F_{li}}&{\bf F_{lj}}&{\bf F_{lm}} \end{pmatrix}^T = \begin{pmatrix} F_{Lix}&F_{Liy}&F_{Ljx}&F_{Ljy}&F_{Lmx}&F_{Lmy} \end{pmatrix}^T\]
单元上各结点虚位移为: \( {\bf (\delta^*)^e} = \begin{pmatrix} u^*_i&v^*_i&u^*_j&v^*_j&u^*_m&v^*_m \end{pmatrix}^T \)
由 \( (6) \) 得,集中力作用点(x,y)的虚位移为: \( {{\bf d^* = N(\delta^*)^e}} \)
根据静力等效原则,移置的结点载荷在结点虚位移上的虚功,应当等于原载荷(集中力)在其作用点的虚位移上的虚功:
\[(({\bf \delta}^*)^e)^T {\bf F}^e_L = {\bf d}^*{\bf f}_pt\]
代入相关值:
\[(({\bf \delta}^*)^e)^T{\bf F}^e_L = ({\bf N(\delta^*)^e})^Tf_pt = ({\bf ((\delta^*)^e)^T N^T} f_p t\]
虚位移是任意的,因此其余部分必须相等:
\[{\bf F}^e_L = {\bf N}^T f_p t\]
这就是集中力的移置公式。
3.5.2 体力的移置公式
与集中力相似,可建立体力 \( {\bf f} = \begin{pmatrix} f_x & f_y \end{pmatrix}^T \) 的移置公式:
\[{\bf F}^e_L = t \iint_A {\bf N}^T {\bf f} \,{\rm d}x{\rm d}y\]
对于自重体力 \( f_x = 0 , f_y = -\rho g \) :
\[{\bf F}^e_L = \begin{pmatrix} F_{Lix}& F_{Liy} & F_{Ljx} & F_{Ljy} & F_{Lmx} & F_{Lmy} \end{pmatrix}^T =\\ \begin{pmatrix} 0&0&0&-\frac{1}{3}\rho gtA&-\frac{1}{3}\rho gtA&-\frac{1}{3}\rho gtA \end{pmatrix}^T\]
3.5.3 面力的移置公式
同理可得面力 \( \overline{\bf f} = \begin{pmatrix} \overline{f_x} & \overline{f_y} \end{pmatrix}^T \) 移置公式:
\[{\bf F}^e_L = t \int_{s_\sigma} {\bf N}^T \overline{\bf f} \,{\rm d}x{\rm d}y\]
3.6 建立结点平衡方程:
以结点为研究对象,结点i受结点力( \( {\bf -F}_i \) )和节点载荷( \( {\bf F_{Li}} \) )。结点平衡,所有外力之和为零。即:
\[\sum_e {\bf F}_i = \sum_e {\bf F}_{Li}\]
注意,结点除受前面研究的单元的结点力和移置载荷,还会收到别的相邻单元的结点力反和移置载荷, \( \sum_e \) 是对围绕结点i的所有单元的求和。
3.7 组合结点、建立整体平衡方程:
前面几部都是将一个个单元分开来考虑,建立起了单元上的几个结点的平衡方程。接下来将所有的单元以结点的方式连接起来,建立整体平衡方程。
整体平衡方程是所有单元上的外载荷移置到其中任意一个结点v的结点载荷 \( {\bf F_{Lv}} \) 和所有单元对结点v的结点力 \( \bf -F_v \) 相平衡。
在有限元素法中,将结点力表示为位移模式(用单元结点位移表示,即式 \( (7) \) )。所以从数学角度来说, \( \bf -F_v \) 是所有单元上的所有结点位移引起的对结点v的结点力。
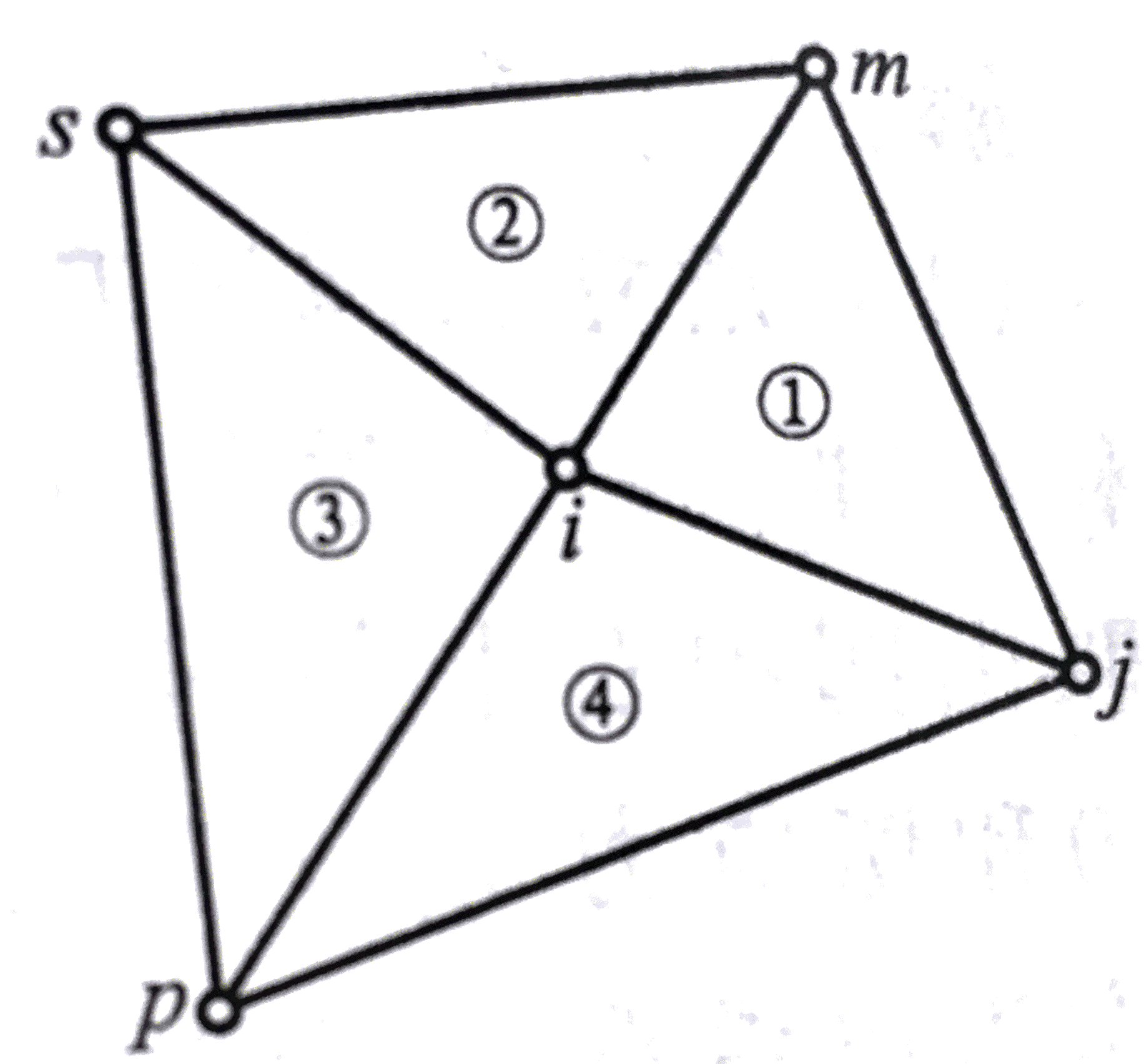
如图所示:结点i四周有单元①、②、③、④相连,与结点j、m、s、p相连。可以看出结点j的位移可以通过单元①和单元②作用于结点i,产生结点力,所以要计算结点j位移引起的对i的结点力,需要将这两个方式产生的结点力相叠加。下面操作一下:
现在我们研究单元①对结点i的结点力。查看式 \( (7) \) ,将这个矩阵方程展开:
\[\begin{pmatrix} F^①_{ix}\\ F^①_{iy}\\ F^①_{jx}\\ F^①_{jy}\\ F^①_{mx}\\ F^①_{my}\end{pmatrix} = \begin{pmatrix} k^①_{(ix)(ix)}&k^①_{(ix)(iy)}&k^①_{(ix)(jx)}&k^①_{(ix)(jy)}&k^①_{(ix)(mx)}&k^①_{(ix)(my)}\\ k^①_{(iy)(ix)}&k^①_{(iy)(iy)}&k^①_{(iy)(jx)}&k^①_{(iy)(jy)}&k^①_{(iy)(mx)}&k^①_{(iy)(my)}\\ k^①_{(jx)(ix)}&k^①_{(jx)(iy)}&k^①_{(jx)(jx)}&k^①_{(jx)(jy)}&k^①_{(jx)(mx)}&k^①_{(jx)(my)}\\ k^①_{(jy)(ix)}&k^①_{(jy)(iy)}&k^①_{(jy)(jx)}&k^①_{(jy)(jy)}&k^①_{(jy)(mx)}&k^①_{(jy)(my)}\\ k^①_{(mx)(ix)}&k^①_{(mx)(iy)}&k^①_{(mx)(jx)}&k^①_{(mx)(jy)}&k^①_{(mx)(mx)}&k^①_{(mx)(my)}\\ k^①_{(my)(ix)}&k^①_{(my)(iy)}&k^①_{(my)(jx)}&k^①_{(my)(jy)}&k^①_{(my)(mx)}&k^①_{(my)(my)}\\\end{pmatrix}\begin{pmatrix} \delta_{ix}\\ \delta_{iy}\\ \delta_{jx}\\ \delta_{jy}\\ \delta_{mx}\\ \delta_{my}\end{pmatrix}\]
取出其中与作用于结点i的结点力相关的部分:
\[\begin{pmatrix} F^①_{ix}\\ F^①_{iy}\end{pmatrix} = \begin{pmatrix} k^①_{(ix)(ix)}&k^①_{(ix)(iy)}&k^①_{(ix)(jx)}&k^①_{(ix)(jy)}&k^①_{(ix)(mx)}&k^①_{(ix)(my)}\\ k^①_{(iy)(ix)}&k^①_{(iy)(iy)}&k^①_{(iy)(jx)}&k^①_{(iy)(jy)}&k^①_{(iy)(mx)}&k^①_{(iy)(my)}\end{pmatrix}\begin{pmatrix} \delta_{ix}\\ \delta_{iy}\\ \delta_{jx}\\ \delta_{jy}\\ \delta_{mx}\\ \delta_{my}\end{pmatrix}\]
同理我们研究单元②、③、④对结点i的结点力:
\[\begin{pmatrix} F^②_{ix}\\ F^②_{iy}\end{pmatrix} = \begin{pmatrix} k^②_{(ix)(ix)}&k^②_{(ix)(iy)}&k^②_{(ix)(sx)}&k^②_{(ix)(sy)}&k^②_{(ix)(mx)}&k^②_{(ix)(my)}\\ k^②_{(iy)(ix)}&k^②_{(iy)(iy)}&k^②_{(iy)(sx)}&k^②_{(iy)(sy)}&k^②_{(iy)(mx)}&k^②_{(iy)(my)}\end{pmatrix}\begin{pmatrix} \delta_{ix}\\ \delta_{iy}\\ \delta_{sx}\\ \delta_{sy}\\ \delta_{mx}\\ \delta_{my}\end{pmatrix}\]
\[\begin{pmatrix} F^③_{ix}\\ F^③_{iy}\end{pmatrix} = \begin{pmatrix} k^③_{(ix)(ix)}&k^③_{(ix)(iy)}&k^③_{(ix)(sx)}&k^③_{(ix)(sy)}&k^③_{(ix)(px)}&k^③_{(ix)(py)}\\ k^③_{(iy)(ix)}&k^③_{(iy)(iy)}&k^③_{(iy)(sx)}&k^③_{(iy)(sy)}&k^③_{(iy)(px)}&k^③_{(iy)(py)}\end{pmatrix}\begin{pmatrix} \delta_{ix}\\ \delta_{iy}\\ \delta_{sx}\\ \delta_{sy}\\ \delta_{px}\\ \delta_{py}\end{pmatrix}\]
\[\begin{pmatrix} F^④_{ix}\\ F^④_{iy}\end{pmatrix} = \begin{pmatrix} k^④_{(ix)(ix)}&k^④_{(ix)(iy)}&k^④_{(ix)(jx)}&k^④_{(ix)(jy)}&k^④_{(ix)(px)}&k^④_{(ix)(py)}\\ k^④_{(iy)(ix)}&k^④_{(iy)(iy)}&k^④_{(iy)(jx)}&k^④_{(iy)(jy)}&k^④_{(iy)(px)}&k^④_{(iy)(py)}\end{pmatrix}\begin{pmatrix} \delta_{ix}\\ \delta_{iy}\\ \delta_{jx}\\ \delta_{jy}\\ \delta_{px}\\ \delta_{py}\end{pmatrix}\]
上面的方程矩阵庞大,我们将其分块。以单元①的为例,将同一结点的不同坐标的元素划为一个子矩阵:
\[\begin{pmatrix} F^①_{ix}\\ F^①_{iy}\end{pmatrix} = \begin{pmatrix} \begin{array}{cc|cc|cc} k^①_{(ix)(ix)}&k^①_{(ix)(iy)}&k^①_{(ix)(jx)}&k^①_{(ix)(jy)}&k^①_{(ix)(mx)}&k^①_{(ix)(my)}\\ k^①_{(iy)(ix)}&k^①_{(iy)(iy)}&k^①_{(iy)(jx)}&k^①_{(iy)(jy)}&k^①_{(iy)(mx)}&k^①_{(iy)(my)} \end{array}\end{pmatrix}\begin{pmatrix} \delta_{ix}\\ \delta_{iy}\\ \hline \delta_{jx}\\ \delta_{jy}\\ \hline \delta_{mx}\\ \delta_{my}\end{pmatrix}\]
简写为:
\[{\bf F^①_i} = \begin{pmatrix} {\bf k}^①_{ii}&{\bf k}^①_{ij}&{\bf k}^①_{im}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\\end{pmatrix}\]
同理可得其余三个单元的结点力方程:
\[{\bf F^②_i} = \begin{pmatrix} {\bf k}^②_{ii}&{\bf k}^②_{is}&{\bf k}^②_{im}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_s\\ {\bf \delta}_m\\\end{pmatrix}\]
\[{\bf F^③_i} = \begin{pmatrix} {\bf k}^③_{ii}&{\bf k}^③_{is}&{\bf k}^③_{ip}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_s\\ {\bf \delta}_p\\\end{pmatrix}\]
\[{\bf F^④_i} = \begin{pmatrix} {\bf k}^④_{ii}&{\bf k}^④_{ij}&{\bf k}^④_{ip}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_p\\\end{pmatrix}\]
将所有单元的结点力相累加:
\[{\bf F_i} = \begin{pmatrix} {\bf k}^①_{ii}+{\bf k}^②_{ii}+{\bf k}^③_{ii}+{\bf k}^④_{ii}& {\bf k}^④_{ij}+{\bf k}^①_{ij}& {\bf k}^①_{im}+{\bf k}^②_{im}& {\bf k}^②_{is}+{\bf k}^③_{is}& {\bf k}^③_{ip}+{\bf k}^④_{ip}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\ {\bf \delta}_s\\ {\bf \delta}_p\end{pmatrix}\]
通过上面的方程可以看出,结点i的位移通过单元①②③④对结点i产生结点力。结点j的位移通过单元④①对结点i产生结点力。结点m的位移通过单元①②对结点i产生结点力。结点s的位移通过单元②③对结点i产生结点力。结点p的位移通过单元③④对结点i产生结点力。这与图中所示的结构相符。
继续将上面的方程简写:
\[{\bf F_i} = \begin{pmatrix} \sum{\bf k}_{ii}& \sum{\bf k}_{ij}& \sum{\bf k}_{im}& \sum{\bf k}_{is}& \sum{\bf k}_{ip}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\ {\bf \delta}_s\\ {\bf \delta}_p\end{pmatrix}\]
其中 \( \sum \) 表示将所有单元的结点力方程系数矩阵中下标相同的子矩阵叠加。若简化前的方程中的的子矩阵没有对应的项,则该项为0。比如: \( \sum{\bf k}_{ij} = {\bf k}^④_{ij}+{\bf k}^①_{ij} + 0 + 0 \) 。
以上将整体对i结点的结点力表示出来。而整体平衡方程是建立所有结点的平衡条件,所以还需要表示出其他的结点的结点力。即:
\[{\bf F_j} = \begin{pmatrix} \sum{\bf k}_{ji}& \sum{\bf k}_{jj}& \sum{\bf k}_{jm}& \sum{\bf k}_{js}& \sum{\bf k}_{jp}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\ {\bf \delta}_s\\ {\bf \delta}_p\end{pmatrix}\]
\[{\bf F_m} = \begin{pmatrix} \sum{\bf k}_{mi}& \sum{\bf k}_{mj}& \sum{\bf k}_{mm}& \sum{\bf k}_{ms}& \sum{\bf k}_{mp}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\ {\bf \delta}_s\\ {\bf \delta}_p\end{pmatrix}\]
\[{\bf F_s} = \begin{pmatrix} \sum{\bf k}_{si}& \sum{\bf k}_{sj}& \sum{\bf k}_{sm}& \sum{\bf k}_{ss}& \sum{\bf k}_{sp}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\ {\bf \delta}_s\\ {\bf \delta}_p\end{pmatrix}\]
\[{\bf F_p} = \begin{pmatrix} \sum{\bf k}_{pi}& \sum{\bf k}_{pj}& \sum{\bf k}_{pm}& \sum{\bf k}_{ps}& \sum{\bf k}_{pp}\end{pmatrix}\begin{pmatrix} {\bf \delta}_i\\ {\bf \delta}_j\\ {\bf \delta}_m\\ {\bf \delta}_s\\ {\bf \delta}_p\end{pmatrix}\]
将上面的五个矩阵方程组合起来:
\[{\bf F = K\delta} \tag{8}\]
其中:
\[{\bf F} = \begin{pmatrix} {\bf F}_i &{\bf F}_j & {\bf F}_m & {\bf F}_s & {\bf F}_p \end{pmatrix}^T\]
\[{\bf K} = \begin{pmatrix} \sum{\bf k}_{ii}&\sum{\bf k}_{ij}&\sum{\bf k}_{im}&\sum{\bf k}_{is}&\sum{\bf k}_{ip}\\ \sum{\bf k}_{ji}&\sum{\bf k}_{jj}&\sum{\bf k}_{jm}&\sum{\bf k}_{js}&\sum{\bf k}_{jp}\\ \sum{\bf k}_{mi}&\sum{\bf k}_{mj}&\sum{\bf k}_{mm}&\sum{\bf k}_{ms}&\sum{\bf k}_{mp}\\ \sum{\bf k}_{si}&\sum{\bf k}_{sj}&\sum{\bf k}_{sm}&\sum{\bf k}_{ss}&\sum{\bf k}_{sp}\\ \sum{\bf k}_{pi}&\sum{\bf k}_{pj}&\sum{\bf k}_{pm}&\sum{\bf k}_{ps}&\sum{\bf k}_{pp}\end{pmatrix}\]
\[{\bf \delta} =\begin{pmatrix} {\bf \delta}_i&{\bf \delta}_j&{\bf \delta}_m&{\bf \delta}_s&{\bf \delta}_p\end{pmatrix}^T\]
对于整体来说,整体的结点载荷应该和整体的结点力相平衡,即:
\[{\bf F = F_L}\]
其中:
\[{\bf F}_L = \begin{pmatrix} {\bf F}_{Li} &{\bf F}_{Lj} & {\bf F}_{Lm} & {\bf F}_{Ls} & {\bf F}_{Lp} \end{pmatrix}^T\]
代入 \( (8) \) 中:
\[{\bf F}_L = {\bf K \delta} \tag{9}\]
这就是整体平衡方程。
注意:这里的结点载荷包括了边界结点的约束力。书中并没有把约束力划入结点载荷中,这从理论上不对的。尽管求解时,由于会简化劲度矩阵,将约束力相关行删去,最后也能得出正确答案。但如果把求得位移代入原方程中,就会发现方程不成立。详细原因可以点这里。
3.8 结合利用边界条件简化平衡方程:
位移边界条件规定了相应结点的位移为零。于是减少了未知数,可以简化整体平衡方程。
下面以一个实际例子操作一下。
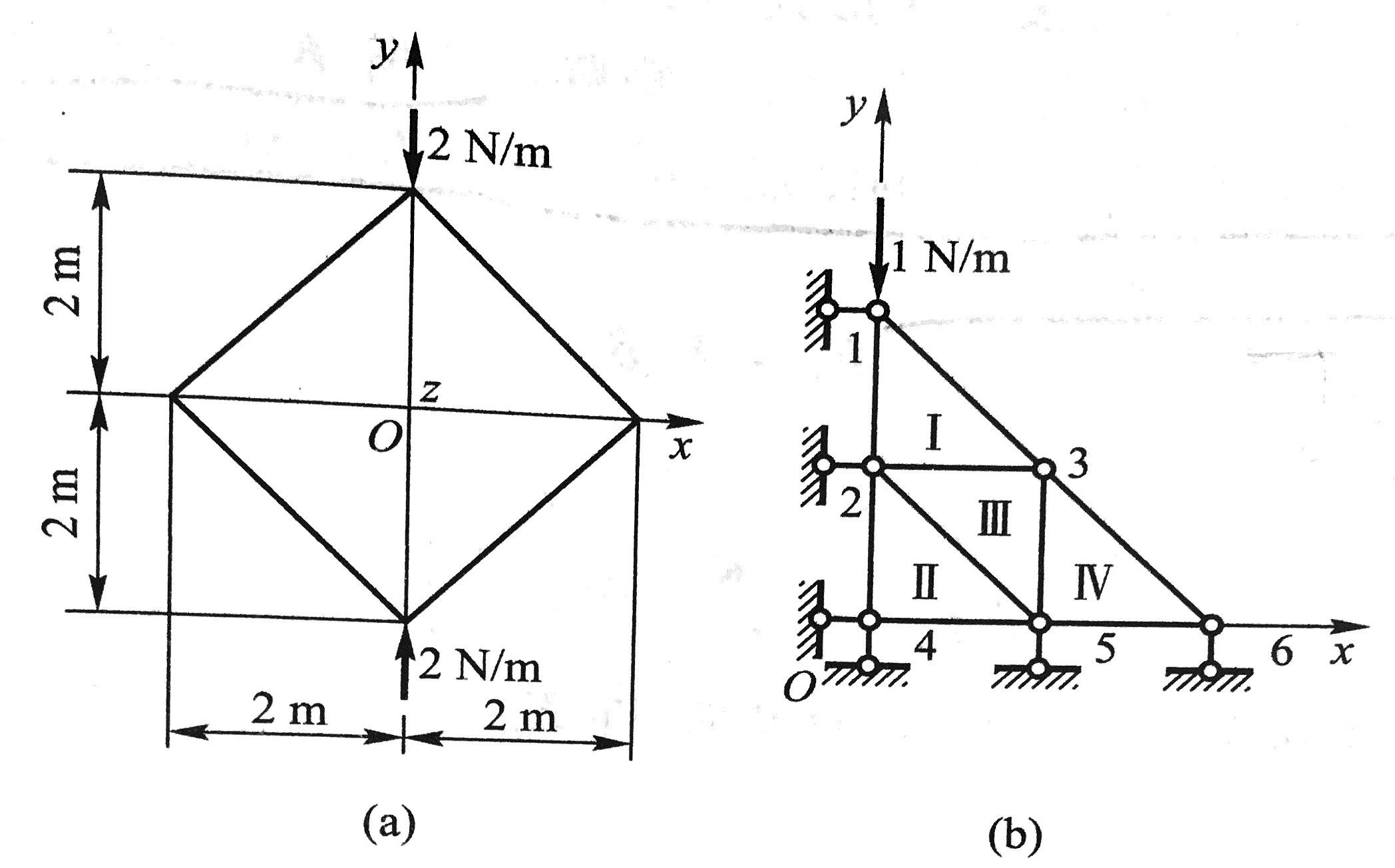
如图所示(a),一个正方形薄板。一对顶角受集中力压。
利用对称条件简化,研究其1/4部分,并将其划分网格,如图中(b)所示。将其划分为单元Ⅰ、Ⅱ、Ⅲ、Ⅳ,产生结点1、2、3、4、5、6。各结点边界条件如图所示。
易得结点载荷为:
\[{\bf F}_L = \\\begin{pmatrix} F_{L1x}&F_{L1y}&F_{L2x}&F_{L2y}&F_{L3x}&F_{L3y}&F_{L4x}&F_{L4y}&F_{L5x}&F_{L5y}&F_{L6x}&F_{L6y}\end{pmatrix}^T \\=\begin{pmatrix} F_{L1x}&-1&F_{L2x}&0&0&0&F_{L4x}&F_{L4y}&0&F_{L5y}&0&F_{L6y}\end{pmatrix}^T\]
其中有6个约束力未知。
在边界条件的约束下,结点位移为:
\[{\bf \delta} = \\\begin{pmatrix} \delta_{1x}&\delta_{1y}&\delta_{2x}&\delta_{2y}&\delta_{3x}&\delta_{3y}&\delta_{4x}&\delta_{4y}&\delta_{5x}&\delta_{5y}&\delta_{6x}&\delta_{6y}\end{pmatrix}^T \\= \begin{pmatrix} 0&v_1&0&v_2&u_3&v_3&0&0&u_5&0&u_6&0\end{pmatrix}^T\]
整体劲度矩阵为(取 \( \tau = 0,t = 1 \) ):
\[{\bf K} = E\begin{pmatrix} 0.25&0&-0.25&-0.25&0&0.25&0&0&0&0&0&0\\ 0&0.5&0&-0.5&0&0&0&0&0&0&0&0\\ -0.25&0&1.5&0.25&-1&-0.25&-0.25&-0.25&0&0.25&0&0\\ -0.25&-0.5&0.25&1.5&-0.25&-0.5&0&-0.5&0.25&0&0&0\\ 0&0&-1&-0.25&1.5&0.25&0&0&-0.5&-0.25&0&0.25\\ 0.25&0&-0.25&-0.5&0.25&1.5&0&0&-0.25&-1&0&0\\ 0&0&-0.25&0&0&0&0.75&0.25&-0.5&-0.25&0&0\\ 0&0&0.25&-0.5&0&0&0.25&0.75&0&-0.25&0&0\\ 0&0&0&0.25&-0.5&-0.25&-0.5&0&1.5&0.25&-0.5&-0.25\\ 0&0&0.25&0&-0.25&-1&-0.25&-0.25&0.25&1.5&0&-0.25\\ 0&0&0&0&0&0&0&0&-0.5&0&0.5&0\\ 0&0&0&0&0.25&0&0&0&-0.25&-0.25&0&0.25\end{pmatrix}\]
三个矩阵满足 \( (9) \) 式。
在结点位移矩阵中: \( \delta_{1x}=\delta_{2x}=\delta_{4x}=\delta_{4y}=\delta_{5y}=\delta_{6y}=0 \) 。于是系数矩阵 \( {\bf K} \) 矩阵中第1、3、7、8、10、12列与之相乘一定为零,故将这几列删去。另一方面,这几个位移刚好对应于几个未知的约束力。可以利用将这几个位移代入方程求得未知的约束力。于是删去系数矩阵 \( {\bf K} \) 和常数项矩阵 \( {\bf F}_L \) 中第1、3、7、8、10、12行。于是矩阵方程可化简为:
\[E\begin{pmatrix} 0.5&-0.5&0&0&0&0\\ -0.5&1.5&-0.25&-0.5&0.25&0\\ 0&-0.25&1.5&0.25&-0.5&0\\ 0&-0.5&0.25&1.5&-0.25&0\\ 0&0.25&-0.5&-0.25&1.5&-0.5\\ 0&0&0&0&-0.5&0.5\end{pmatrix}\begin{pmatrix} v_1\\v_2\\u_3\\v_3\\u_5\\u_6\end{pmatrix} = \begin{pmatrix} -1\\0\\0\\0\\0\\0\end{pmatrix}\]
3.9 求解出结点位移进而求得应力应变:
通过以上步骤,可以解得结点位移。将每个单元中的结点位移代入各自的 \( (3) \) 式和 \( (5) \) 式。即可求得所有单元应力应变。
至此,有限元素法完成运算。
4、注意
本笔记中的有限元单元法是工程中最简单的模型。其中包含了许多的最简单的情况。比如,单元为三角形单元(常应变单元),使得形函数矩阵简单、劲度矩阵元素不含积分。本构关系采用了最简单的广义胡克定律。
本文章使用limfx的vsocde插件快速发布









