均匀弦动力学涉猎

• 均匀弦动力学涉猎

  • 1 绪论

  • 2 模型建立与化简

    • 2.1 模型建立

    • 2.2 模型化简

  • 3 方程求解与振型模态的概念

    • 3.1 方程的通解

    • 3.2 振型模态

    • 3.3 模态振型的正交性的证明

    • 3.4 模态振型正交性的使用

  • 4 弦振动的另一种解释——行波

  • 5 广义运动方程

    • 5.1 广义坐标

    • 5.2 广义运动方程

      • 5.2.1 弦的势能

      • 5.2.2 弦的动能

      • 5.2.3 弦的广义力

      • 5.2.4 广义运动方程的推导

    • 5.3 广义运动方程求解实例

  • 6 总结

1 绪论

弦振动是生活中常见的实际问题，均匀弦是其中比简单一种情况。本文将研究均匀弦自由振动的动力学方程，求解方程并引出振型模态和振动广义自由度的概念。推出弦振动的广义运动方程，进而推广到均匀弦非自由振动的情况。

本文涉及到的知识有，但不限于：理论力学、材料力学、高等数学、线性代数。

注：书中所列的公式博主都尽量推了一遍。然而由于数学功底不足，对于书中一少部分简略了的公式步骤任然没能推出。它们后面均以“(?)”标注。请读者讨论。

2 模型建立与化简

2.1 模型建立

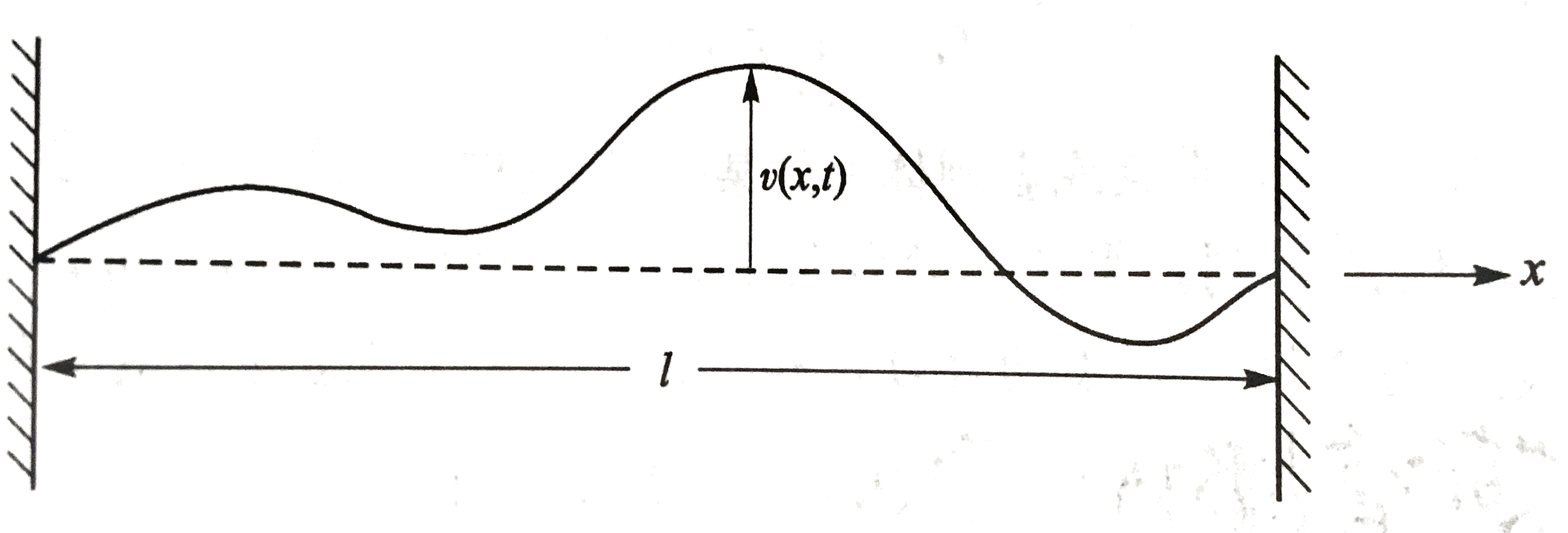
如图所示，一个初始长为$l_0$的弦在x方向被拉伸，固定于两墙之间，墙的距离为$l$，大于$l_0$。x处t时刻，横向位移表示为$v(x,t)$，纵向位移表示为$u(x,t)$。

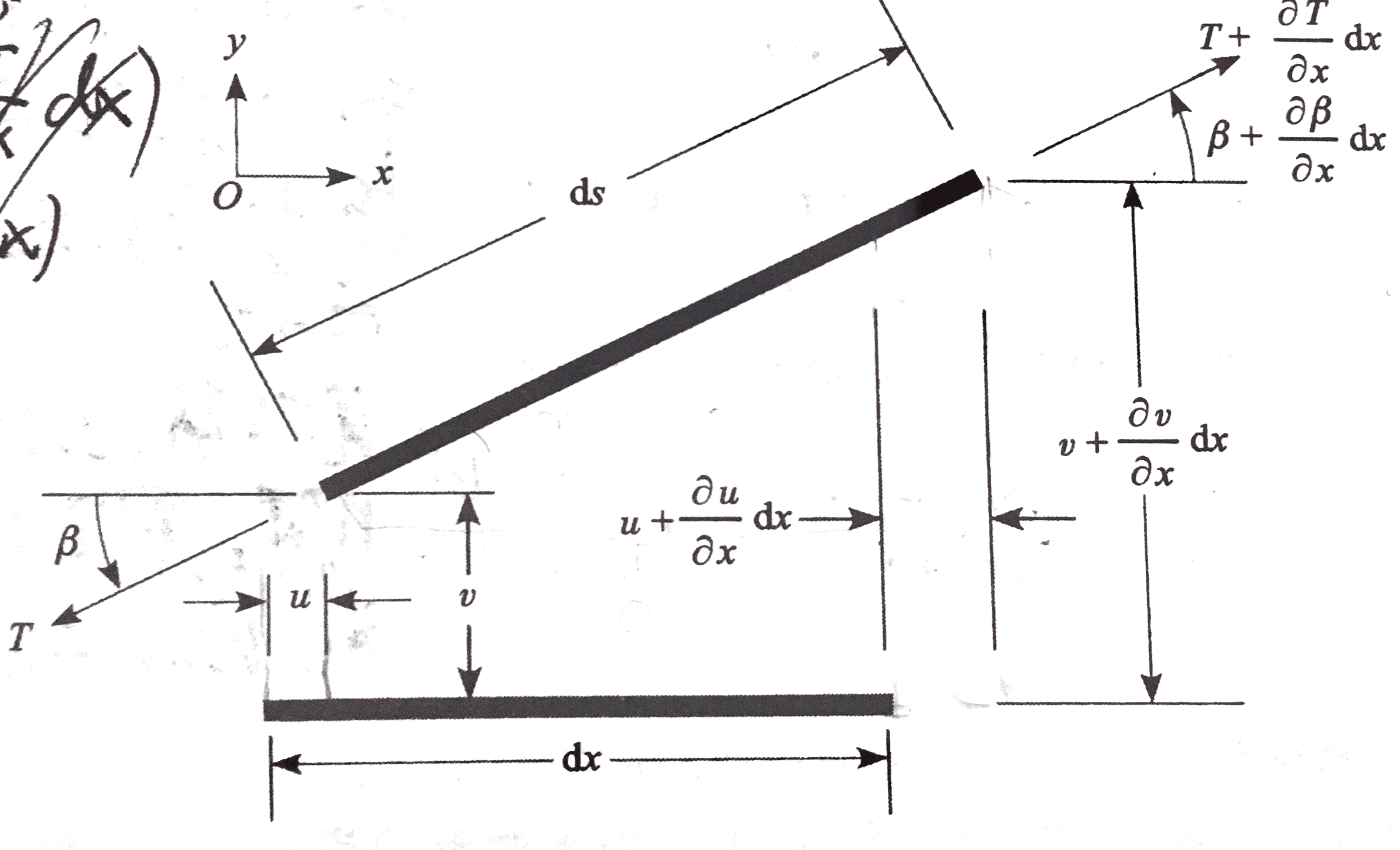
取出一段微元，如图所示：

微元忽略二阶以上的级数。此微元质量为$mdx$，其中$m$为线密度。$T$为左侧弦拉力。$\beta$为左侧弦切线与x轴夹角。

由质心运动定理，并投影到x和y方向得：

$$\sum F_x=mdx{a}_{cx},\sum F_y=mdx{a}_{cy}\text{\hspace{1em}(2.1.1)}$$

其中：

$$\sum F_x=(T+\frac{\partial T}{\partial x}dx)\mathrm{c}\mathrm{o}\mathrm{s}(\beta +\frac{\partial \beta }{\partial x}dx)-T\mathrm{c}\mathrm{o}\mathrm{s}\beta$$

由于弦为微振动：

$$\mathrm{c}\mathrm{o}\mathrm{s}(\beta +\frac{\partial \beta }{\partial x}dx)\approx \mathrm{c}\mathrm{o}\mathrm{s}\beta$$

则：

$$\sum F_x=\frac{\partial T}{\partial x}dx\mathrm{c}\mathrm{o}\mathrm{s}\beta$$

另外：

$$\frac{\partial }{\partial x}(T\mathrm{c}\mathrm{o}\mathrm{s}\beta )=\frac{\partial T}{\partial x}\mathrm{c}\mathrm{o}\mathrm{s}\beta -\mathrm{s}\mathrm{i}\mathrm{n}\beta \frac{\partial \beta }{\partial x}T\approx \frac{\partial T}{\partial x}\mathrm{c}\mathrm{o}\mathrm{s}\beta (其中\mathrm{s}\mathrm{i}\mathrm{n}\beta \approx 0)$$

于是：

$$\sum F_x=\frac{\partial }{\partial x}(T\mathrm{c}\mathrm{o}\mathrm{s}\beta )dx\text{\hspace{1em}(2.1.2)}$$

另一方面：

$$u_c=\frac{u+(u+\frac{\partial u}{\partial x}dx)}{2}=u+\frac{1}{2}\frac{\partial u}{\partial x}dx\approx u$$

故：

$$a_{cx}=\frac{{\partial }^{2}u}{\partial t^2}\text{\hspace{1em}(2.1.3)}$$

将$(2.1.2),(2.1.3)$代入$(2.1.1)$的前一式中：

$$\frac{\partial }{\partial x}(T\mathrm{c}\mathrm{o}\mathrm{s}\beta )=m\frac{{\partial }^{2}u}{\partial t^2}\text{\hspace{1em}(2.1.4)}$$

同理，对于$(2.1.1)$的后一式有类似的推导：

$$\frac{\partial }{\partial x}(T\mathrm{s}\mathrm{i}\mathrm{n}\beta )=m\frac{{\partial }^{2}v}{\partial t^2}(?)\text{\hspace{1em}(2.1.5)}$$

设应变为$ϵ$,由图可看出$ϵ=\frac{ds-dx}{dx}$，即$ds=(1+ϵ)dx$。

如图中的几何关系：

$$\mathrm{s}\mathrm{i}\mathrm{n}\beta =\frac{(v+\frac{\partial v}{\partial x}dx)-v}{ds}=\frac{1}{1+ϵ}\frac{\partial v}{\partial x}\text{\hspace{1em}(2.1.6)}$$

$$\mathrm{c}\mathrm{o}\mathrm{s}\beta =\frac{dx-u+u+\frac{\partial u}{\partial x}dx}{ds}=\frac{1}{1+ϵ}(1+\frac{\partial u}{\partial x})\text{\hspace{1em}(2.1.7)}$$

因为${\mathrm{c}\mathrm{o}\mathrm{s}}^2\beta +{\mathrm{s}\mathrm{i}\mathrm{n}}^2\beta =1$,则

$$ϵ=\sqrt{(1+\frac{\partial u}{\partial x}{)}^2+(\frac{\partial v}{\partial x}{)}^2}-1\text{\hspace{1em}(2.1.8)}$$

设$EA$为弦的纵向刚度，由材料力学可知：

$$T=EAϵ\text{\hspace{1em}(2.1.9)}$$

同时补充边界条件，即弦两端位移恒为零：

$$v(0,t)=v(l,t)=0\text{\hspace{1em}(2.1.10)}$$

至此，从$(2.1.4)$到$(2.1.10)$为弦自由振动系统的数学模型。

2.2 模型化简

假设弦变形存在一个静平衡解，该解的所有函数与时间$t$无关，即：

$$\begin{array}{c}u(x,t)=\overline{u}(x)\\ v(x,t)=0\\ \beta (x,t)=0\\ ϵ(x,t)=\overline{ϵ}(x)\\ T(x,t)=\overline{T}(x)\end{array}\}$$

将上面方程代入$(2.1.4)、(2.1.5)$，且由边界条件$\overline{u}(0)=0$得：

$$\begin{array}{c}\overline{T}(x)=T_0\\ \overline{ϵ}(x)={ϵ}_0=\frac{T_0}{EA}=\frac{l-l_0}{l}\\ \overline{u}(x)={ϵ}_{0}x\end{array}\}$$

静平衡方程中$T_0$相当大，则振动变形较小，可看成摄动量，因此可假设：

$$\begin{array}{c}u(x,t)={ϵ}_{0}x+u(x,t)\\ v(x,t)=v(x,t)\\ \beta (x,t)=\beta (x,t)\\ ϵ(x,t)={ϵ}_0+ϵ(x,t)\\ T(x,t)=T_0+T(x,t)\end{array}\}\text{\hspace{1em}(2.2.1)}$$

另外，由于变形较小，$\beta =\mathrm{s}\mathrm{i}\mathrm{n}\beta$，参照$(2.1.6)$：

$$\beta =\frac{1}{1+{ϵ}_0}\frac{\partial v}{\partial x}\text{\hspace{1em}(2.2.2)}$$

将$(2.2.1)$和$(2.2.2)$代入$(2.1.4)$和$(2.1.5)$中，忽略所有摄动量平方项和相乘项，得：

$$\begin{array}{c}EA\frac{{\partial }^{2}u}{\partial x^2}=m\frac{{\partial }^{2}u}{\partial t^2}(?)\\ \frac{T_0}{1+{ϵ}_0}\frac{{\partial }^{2}v}{\partial x^2}=m\frac{{\partial }^{2}v}{\partial t^2}\end{array}\}\text{\hspace{1em}(2.2.3)}$$

由于$EA\gg T_0$所以纵向幅值非常小，不是我们感兴趣的。结合$(2.1.9)$可以看出${ϵ}_0\ll 1$，因此上方程组第二项可写成：

$$T_0\frac{{\partial }^{2}v}{\partial x^2}=m\frac{{\partial }^{2}v}{\partial t^2}$$

去掉摄动量上标，得：

$$T\frac{{\partial }^{2}v}{\partial x^2}=m\frac{{\partial }^{2}v}{\partial t^2}\text{\hspace{1em}(2.2.4)}$$

这就是简化后的弦自由振动方程。

3 方程求解与振型模态的概念

3.1 方程的通解

对于弦自由振动方程$(2.2.4)$，可以构造出解的形式，进而分离变量。

令：

$$v(x,t)=X(x)Y(t)\text{\hspace{1em}(3.1.1)}$$

代入$(2.2.4)$，整理得：

$$\frac{T{X}^{\prime \prime }(x)}{mX(x)}=\frac{\ddot{Y}(t)}{Y(t)}$$

上式中，因为方程两边各自为不同的独立变量的函数，方程成立的唯一方式是两边都等于同一个常数，令这个常数为$-{\omega }^2$。则有：

$$\begin{array}{c}T{X}^{\prime \prime }(x)+m{\omega }^{2}X(x)=0\\ \ddot{Y}(t)+{\omega }^{2}Y(t)=0\end{array}\}$$

令:

$${\alpha }^2=\frac{m{\omega }^2}{T}\text{\hspace{1em}(3.1.2)}$$

则:

$$\begin{array}{c}{X}^{\prime \prime }(x)+{\alpha }^{2}X(x)=0\\ \ddot{Y}(t)+{\omega }^{2}Y(t)=0\end{array}\}$$

于是可解出以上两个方程的通解：

$$\begin{array}{c}X(x)=A\mathrm{s}\mathrm{i}\mathrm{n}(\alpha x)+B\mathrm{c}\mathrm{o}\mathrm{s}(\alpha x)\\ Y(t)=C\mathrm{s}\mathrm{i}\mathrm{n}(\omega t)+D\mathrm{c}\mathrm{o}\mathrm{s}(\omega t)\end{array}\}\text{\hspace{1em}(3.1.3)}$$

其中：

$$\omega =\alpha \sqrt{\frac{T}{m}}\text{\hspace{1em}(3.1.4)}$$

且$\alpha \ne 0$。

则$v(x,t)$的通解为所有$XY$的线性组合。

3.2 振型模态

由边界条件$(2.1.10)$得：

$$\begin{array}{c}X(0)Y(t)=0\\ X(l)Y(t)=0\end{array}\}$$

结合$(3.1.3)$得：

$$\begin{array}{c}B=0\\ A\mathrm{s}\mathrm{i}\mathrm{n}(\alpha l)=0\end{array}\}$$

对上式第二式：当$A=0$时，位移恒为零，即静平衡状态。但我们求的是振动情况，所以$A\ne 0$,于是：

$$\alpha ={\alpha }_i=\frac{i\pi }{l}(i=1,2,\cdots )$$

因此，对于$i$的每个整数值，存在一个特征值${\alpha }_i$和一个与$X_i$关联的解，称为“特征函数”，它构成基于相应$Y_i$的通解，则解可写成：

$$v(x,t)=\sum _{i=1}^{\infty }{v}_i(x,t)=\sum _{i=1}^{\infty }\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})[E_i\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}t)+F_i\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)]\text{\hspace{1em}(3.2.1)}$$

其中：

$${\omega }_i=\frac{i\pi }{l}\sqrt{\frac{T}{m}}$$

观察$(3.2.1)$可以看出，对于任意给定的瞬时，横向变形由无穷个位置函数（是位置$x$的函数）乘上各自对应的时间函数之和。而且每个位置函数和时间函数关联于各自特征函数。这里的位置函数称为“模态振型”。 用${\varphi }_i(x)$表示。对于弦的振动：

$${\varphi }_i(x)=\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\text{\hspace{1em}(3.2.2)}$$

另外，令：

$${\xi }_i(x)=E_i\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}t)+F_i\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)\text{\hspace{1em}(3.2.3)}$$

则，弦振动函数可以表示为：

$$v(x,t)=\sum _{i=1}^{\infty }{\varphi }_i(x){\xi }_i(t)\text{\hspace{1em}(3.2.4)}$$

3.3 模态振型的正交性的证明

所谓正交性即是说，一个函数序列和一个固定积分区间中，所有两个不同函数之积在固定区间的积分为零。

对于均匀弦，模态振型${\varphi }_i(x)$在$(0,l)$上满足正交性。即：

$${\int }_0^l{\varphi }_i(x){\varphi }_j(x)\mathrm{d}x\{\begin{array}{ll}=0& (i\ne j)\\ \ne 0& (i=j)\end{array}$$

而对于非均匀弦，$m(x)$为弦的线密度函数。则有类似的形式：

$${\int }_0^{l}m(x){\varphi }_i(x){\varphi }_j(x)\mathrm{d}x\{\begin{array}{ll}=0& (i\ne j)\\ \ne 0& (i=j)\end{array}$$

下面证明此式：

假设$v_i(x,t)={\varphi }_i(x){\xi }_i(x)$为振动方程的一组特解。代入$(2.2.4)$得：

$$T{\varphi }_i^{\prime \prime }(x){\xi }_i(t)=m(x){\varphi }_i(x)\ddot{{\xi }_i}(t)$$

由于${\xi }_i(x)$为简谐函数，有：

$$\ddot{{\xi }_i}(t)=-{\omega }^2{\xi }_i(t)$$

于是方程变为：

$$T{\varphi }_i^{\prime \prime }(x)=-m(x){\varphi }_i(x){\omega }_i^2\text{\hspace{1em}(3.3.1)}$$

同理，对于另一个特解$v_j(x,t)={\varphi }_j(x){\xi }_j(x)$，有：

$$T{\varphi }_j^{\prime \prime }(x)=-m(x){\varphi }_j(x){\omega }_j^2\text{\hspace{1em}(3.3.2)}$$

$(3.3.1)$乘以${\varphi }_j$，$(3.3.2)$乘以${\varphi }_i$。相减并在$(0,l)$上积分得：

$$({\omega }_i^2-{\omega }_j^2){\int }_0^{l}m(x){\varphi }_i(x){\varphi }_j(x)\mathrm{d}x=T{\int }_0^l[{\varphi }_i(x){\varphi }_j^{\prime \prime }(x)-{\varphi }_i^{\prime \prime }(x){\varphi }_j(x)]\mathrm{d}x$$

右边可利用分部积分，上式可化为：

$$({\omega }_i^2-{\omega }_j^2){\int }_0^{l}m(x){\varphi }_i(x){\varphi }_j(x)\mathrm{d}x=T({\varphi }_i{\varphi }_j^{\prime }-{\varphi }_i^{\prime }{\varphi }_j){|}_0^l-T{\int }_0^l({\varphi }_i^{\prime }{\varphi }_j^{\prime }-{\varphi }_i^{\prime }{\varphi }_j^{\prime })\mathrm{d}x=0$$

当$i\ne j$时，${\omega }_i\ne {\omega }_j$，则有：

$${\int }_0^{l}m(x){\varphi }_i(x){\varphi }_j(x)\mathrm{d}x=0\text{\hspace{1em}(3.3.3)}$$

上式表明两段固定的弦的模态振型构成正交集合。

当$i=j$时，令积分等于$M_i$，即：

$${\int }_0^{l}m(x){\varphi }_i^2(x)\mathrm{d}x=M_i\text{\hspace{1em}(3.3.4)}$$

称为第$i$阶模态的广义质量。

特殊的，对于均匀弦

$${\int }_0^l{\varphi }_i(x){\varphi }_j(x)\mathrm{d}x=0,M_i=\frac{ml}{2}\text{\hspace{1em}(3.3.5)}$$

3.4 模态振型正交性的使用

设均匀弦振动有一初始条件，即初始形状变形和初始速度：

$$\begin{array}{c}v(x,0)=f(x)\\ \frac{\partial v}{\partial t}(x,0)=g(x)\end{array}\}$$

代入$(3.2.1)$得：

$$\begin{array}{c}{\sum }_{i=1}^{\infty }{F}_i\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})=f(x)\\ {\sum }_{i=1}^{\infty }\frac{E_{i}i\pi }{l}\sqrt{\frac{T}{m}}\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})=g(x)\end{array}\}$$

两式分别乘以$\mathrm{s}\mathrm{i}\mathrm{n}(j\pi x/l)\mathrm{d}x$，并沿弦长积分得：

$$\begin{array}{c}{\int }_0^{l}f(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x={\sum }_{i=1}^{\infty }{F}_i{\int }_0^l\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x\\ {\int }_0^{l}g(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x={\sum }_{i=1}^{\infty }\frac{E_{i}i\pi }{l}\sqrt{\frac{T}{m}}{\int }_0^l\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x\end{array}\}$$

利用正交性，即$(3.3.5)$得：

$$\begin{array}{c}{\int }_0^{l}f(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x=F_j{\int }_0^l{\mathrm{s}\mathrm{i}\mathrm{n}}^2(\frac{j\pi x}{l})\mathrm{d}x=\frac{F_{j}l}{2}\\ {\int }_0^{l}g(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x=\frac{E_{i}i\pi }{l}\sqrt{\frac{T}{m}}{\int }_0^l{\mathrm{s}\mathrm{i}\mathrm{n}}^2(\frac{j\pi x}{l})\mathrm{d}x=\frac{E_{j}j\pi }{2}\sqrt{\frac{T}{m}}\end{array}\}$$

解出未知常数得：

$$\begin{array}{c}{E}_i=\frac{2}{i\pi }\sqrt{\frac{m}{T}}{\int }_0^{l}g(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{d}x\\ F_i=\frac{2}{l}{\int }_0^{l}f(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{d}x\end{array}\}\text{\hspace{1em}(3.4.1)}$$

得此初始条件下，弦的振动函数：

$$v(x,t)=\sum _{i=1}^{\infty }\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})[E_i\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}t)+F_i\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)]\text{\hspace{1em}(3.4.2)}$$

4 弦振动的另一种解释——行波

弦的振动也可以看成波的传递，下面推导其数学模型。

假设弦振动的初始条件为，具有初始位移，但初始速度为零。即：

$$\begin{gathered} v(x,0)=f(x) \\ \frac{\partial v}{\partial t}(x,0)=g(x)=0 \end{gathered}$$

结合$(3.4.1)$和$(3.4.2)$得：

$$v(x,t)=\sum _{i=0}^{\infty }\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})F_i\mathrm{c}\mathrm{o}\mathrm{s}(\sqrt{\frac{T}{m}}\frac{i\pi t}{l})\text{\hspace{1em}(4.1)}$$

$$F_i=\frac{2}{l}{\int }_0^{l}f(x)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{d}x\text{\hspace{1em}(4.2)}$$

且

$$v(x,0)=f(x)=\sum _{i=0}^{\infty }{F}_i\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\text{\hspace{1em}(4.3)}$$

由三角函数积化和差公式：

$$\mathrm{s}\mathrm{i}\mathrm{n}\alpha \mathrm{c}\mathrm{o}\mathrm{s}\beta =\frac{1}{2}[\mathrm{s}\mathrm{i}\mathrm{n}(\alpha +\beta )+\mathrm{s}\mathrm{i}\mathrm{n}(\alpha -\beta )]$$

$(4.1)$可写成：

$$v(x,t)=\frac{1}{2}\sum _{i=1}^{\infty }{F}_i\{\mathrm{s}\mathrm{i}\mathrm{n}[\frac{i\pi }{l}(x+\sqrt{\frac{T}{m}}t)]+\mathrm{s}\mathrm{i}\mathrm{n}[\frac{i\pi }{l}(x-\sqrt{\frac{T}{m}}t)]\}$$

代入$(4.3)$得：

$$v(x,t)=\frac{1}{2}[f(x+\sqrt{\frac{T}{m}}t)+f(x-\sqrt{\frac{T}{m}}t)]\text{\hspace{1em}(4.4)}$$

这就是行波的数学模型。

对于以上方程可以做如下解释：

令

$$\begin{array}{c}{x}_L(x,t)\equiv x+\sqrt{\frac{T}{m}}t\\ x_R(x,t)\equiv x-\sqrt{\frac{T}{m}}t\end{array}\}$$

函数变为：

$$v(x,t)=\frac{1}{2}[f(x_L)+f(x_R)]$$

对比$(4.3)$，方程可看为两个波形相叠加后取一半，这两个波形会随时间移动。一个向x正方向移动，一个向x负方向移动。

令：

$$V=\sqrt{\frac{T}{m}}$$

则，$(4.4)$可写为：

$$v(x,t)=\frac{1}{2}[f(x+Vt)+f(x-Vt)]$$

$V$称为传播速度。

由$f(x)$的表达式$(4.3)$可以看出：

1. $f(x)$为奇函数，即$f(-x)=-f(x)$。换句话说，波在墙面$x=0$处具有反射性。

2. $f(x)$是关于x的周期为$2l$的周期函数，即$f(x)=f(x+2nl)(n=0,\pm 1,\pm 2,\cdots )$。结合1可以得出：$f(x+l)=f(x-l)=-f(l-x)$。换句话说，波在墙面$x=l$具有反射性。

注意到物理模型要求$f(x)$的定义域为$(0,l)$。利用上面两条性质可以扩充定义域，让$f(x\pm Vt)$对于任意$t$有定义。即：

当

$$nl\le x+Vt\le (n+1)l(n=0,\pm 1,\pm 2,\cdots )$$

时

$$f(x\pm Vt)=(-1{)}^{n}f\{(-1{)}^n[x\pm Vt+\frac{(-1{)}^n-2n-1}{2}l]\}(?)$$

下面举一实例:

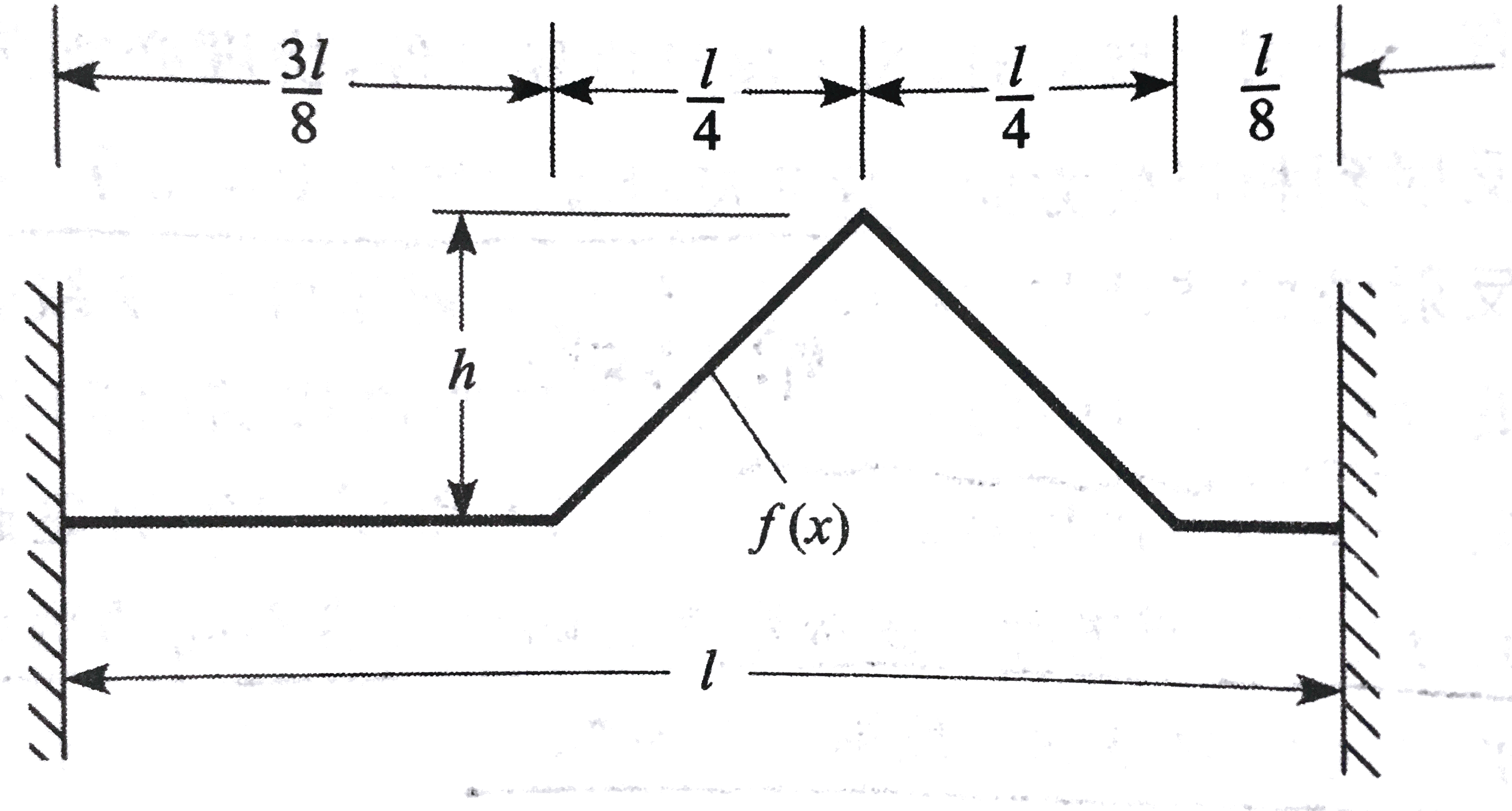
如图所示为弦初始时刻波形图

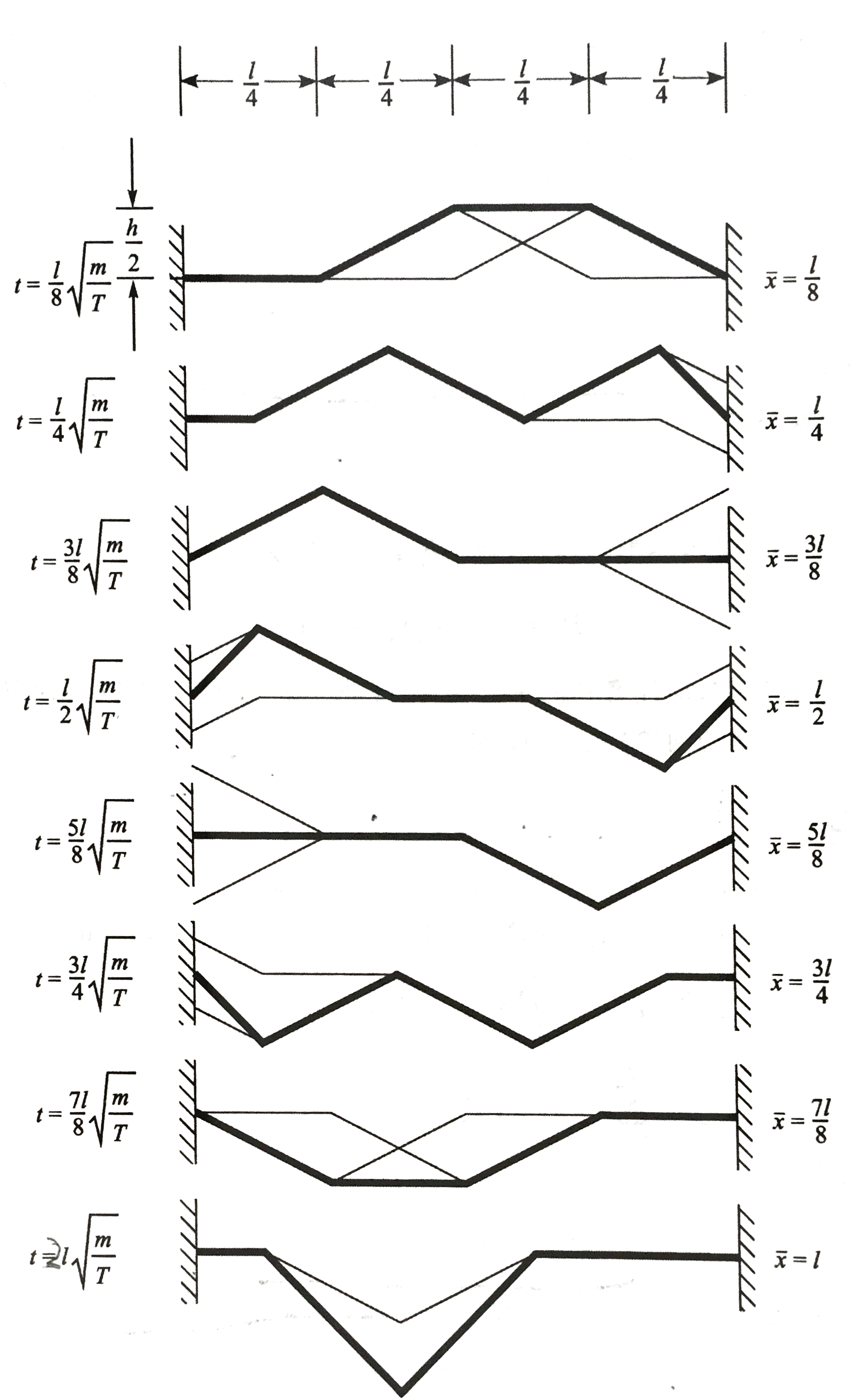
在$t$时刻两个波位移的绝对值用$\overline{x}$表示。如图所示，细线表示两个波的各自位置，粗线表示弦振动行波情况（由两个波合成）。

可以看出波形经过$2l\sqrt{m/T}$后恢复形状。

5 广义运动方程

前面的推导都是弦的自由振动，而实际情况下也有弦受外力的情况下振动，即非自由振动。而非自由振动则需要用广义运动方程求解。

5.1 广义坐标

观察$(3.2.2)$、$(3.2.3)$、$(3.2.4)$：

$${\varphi }_i(x)=\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\text{\hspace{1em}(3.2.2)}$$

$${\xi }_i(x)=E_i\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}t)+F_i\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)\text{\hspace{1em}(3.2.3)}$$

$$v(x,t)=\sum _{i=1}^{\infty }{\varphi }_i(x){\xi }_i(t)\text{\hspace{1em}(3.2.4)}$$

$(3.2.4)$可写为：

$$v(x,t)={\varphi }_1(x){\xi }_1(t)+{\varphi }_2(x){\xi }_2(t)+{\varphi }_3(x){\xi }_3(t)+\cdots$$

写成向量的形式：

$$v(x,t)=\left(\begin{array}{cccc}{\varphi }_1(x)& {\varphi }_2(x)& {\varphi }_3(x)& \cdots \end{array}\right)\left(\begin{array}{c}{\xi }_1(x)\\ {\xi }_2(x)\\ {\xi }_3(x)\\ ⋮\end{array}\right)$$

于是等号右边第二个向量可以看作第一个向量坐标系下的坐标值，即第一个向量代表广义坐标系，第二个向量代表广义坐标。

另外，由3.2节、3.3节、3.4节可以看出，${\varphi }_i(x)$与初始条件无关，${\xi }_i(x)$与初始条件有关。
所以对于弦自由振动问题，一旦其边界条件确定，广义坐标系${\varphi }_i(x)$就随之确定。只需要通过初始条件确定广义坐标${\xi }_i(x)$即可。

而对于非自由振动，其运动函数也可以看出广义坐标系和广义坐标的乘积。（书中没有证明）

5.2 广义运动方程

拉格朗日方程是动力学中普遍适用的方程：

$$\frac{\mathrm{d}}{\mathrm{d}t}(\frac{\partial L}{\partial {\dot{\xi }}_i})-\frac{\partial L}{\partial {\xi }_i}={\Xi }_i(i=1,2,3,\cdots )$$

其中，$L=K-P$为拉格朗日量，即系统总动能$K$和总势能$P$之间的差。${\xi }_i$为广义坐标。${\Xi }_i$为广义力，代表所有非保守力以及没有计入总势能的保守力的作用。

5.2.1 弦的势能

不考虑重力影响，弦的势能考虑为等于其应变能：

$$P=\frac{1}{2}{\int }_0^{l_0}EA{ϵ}^2\mathrm{d}x\text{\hspace{1em}(5.2.1.1)}$$

由2.1节可知：

$$ϵ=\sqrt{(1+\frac{\partial u}{\partial x}{)}^2+(\frac{\partial v}{\partial x}{)}^2}-1\text{\hspace{1em}(2.1.8)}$$

将振动量看成摄动量，由2.2节可知：

$$\begin{array}{c}u(x,t)={ϵ}_{0}x+u(x,t)\\ v(x,t)=v(x,t)\\ \beta (x,t)=\beta (x,t)\\ ϵ(x,t)={ϵ}_0+ϵ(x,t)\\ T(x,t)=T_0+T(x,t)\end{array}\}\text{\hspace{1em}(2.2.1)}$$

$EA$为常值，故$(5.2.1)$可化为：

$$P=\frac{EA}{2}{\int }_0^{l_0}({ϵ}_0^2+2\overline{ϵ}ϵ+{ϵ}^2)\mathrm{d}x\text{\hspace{1em}(5.2.1.2)}$$

由于$T_0=EA{ϵ}_0$。且积分中第一项为常量，可以忽略。（代入拉格朗日方程中，常量不影响方程成立）上式可化为：

$$P=T_0{\int }_0^{l_0}ϵ\mathrm{d}x+\frac{EA}{2}{\int }_0^{l_0}{ϵ}^2\mathrm{d}x$$

由$(2.1.8)$和$(2.2.1)$得：

$$ϵ=\frac{\partial u}{\partial x}+\frac{1}{2(1+{ϵ}_0)}(\frac{\partial v}{\partial x}{)}^2+\cdots (?)$$

代入$(5.2.2)$中省略$\frac{\partial u}{\partial x}$和$\frac{\partial v}{\partial x}$的三次及以上项：

$$P=T_0{\int }_0^{l_0}\frac{\partial u}{\partial x}\mathrm{d}x+\frac{T_0}{2(1+{ϵ}_0)}{\int }_0^{l_0}(\frac{\partial v}{\partial x}{)}^2\mathrm{d}x+\frac{EA}{2}{\int }_0^{l_0}(\frac{\partial u}{\partial x}{)}^2\mathrm{d}x$$

由边界条件得$u(0,t)=u(l,t)=0$，则第一项为零。
由于纵向位移得摄动与横向位移摄动是解耦的，且纵向振动频率非常高，则第三项可以去掉。
又${ϵ}_0\ll 1$。再去掉摄动上标：

$$P=\frac{T_0}{2}{\int }_0^{l_0}(\frac{\partial v}{\partial x}{)}^2\mathrm{d}x$$

代入(3.2.4)得：

$$P=\frac{T_0}{2}{\int }_0^l(\sum _{i=1}^{\infty }{\varphi }_i^{\prime }{\xi }_i{)}^2\mathrm{d}x$$

上式中具有求和的平方，可以写作双重求和的形式，如下面的证明：

$$\begin{array}{rl}(\sum _{i=1}^3{a}_i{)}^2& =(a_1+a_2+a_3{)}^2\\ & =a_1^2+a_2^2+a_3^2+2a_1{a}_2+2a_2{a}_3+2a_3{a}_1\\ & =a_1(a_1+a_2+a_3)+a_2(a_1+a_2+a_3)+a_3(a_1+a_2+a_3)\\ & =a_1\sum _{i=1}^3{a}_i+a_2\sum _{i=1}^3{a}_i+a_3\sum _{i=1}^3{a}_i\\ & =\sum _{j=1}^3{a}_j\sum _{i=1}^3{a}_i\\ & =\sum _{j=1}^3\sum _{i=1}^3{a}_i{a}_j\end{array}$$

于是势能可写为：

$$P=\frac{T}{2}\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\xi }_i{\xi }_j{\int }_0^l{\varphi }_i^{\prime }{\varphi }_j^{\prime }\mathrm{d}x$$

对于弦，振型和它们的一阶导数是正弦函数；因此，它们构成正交集合，即：

$${\int }_0^l{\varphi }_i^{\prime }(x){\varphi }_j^{\prime }(x)\mathrm{d}x=0(i\ne j)$$

则势能化简为：

$$P=\frac{T}{2}\sum _{i=1}^{\infty }{\xi }_i^2{\int }_0^l{\varphi }_i^{\prime 2}\mathrm{d}x$$

利用分部积分：

$${\int }_0^l{\varphi }_i^{\prime }{\varphi }_i^{\prime }\mathrm{d}x={\varphi }_i^{\prime }{\varphi }_i{|}_0^l-{\int }_0^l{\varphi }_i{\varphi }_i^{\prime \prime }\mathrm{d}x$$

由边界条件得：${\varphi }_i(0)={\varphi }_i(l)={\varphi }_i^{\prime }(0)={\varphi }_i^{\prime }(l)$，于是：

$$P=\frac{1}{2}\sum _{i=1}^{\infty }{\xi }_i^2{\int }_0^l-{\varphi }_{i}T{\varphi }_i^{\prime \prime }\mathrm{d}x$$

代入$(3.3.1)$：

$$P=\frac{1}{2}\sum _{i=1}^{\infty }{\xi }_i^2{\int }_0^{l}m(x){\omega }_i{\varphi }_i^2\mathrm{d}x$$

结合$(3.3.4)$得：

$$P=\frac{1}{2}\sum _{i=1}^{\infty }{M}_i{\omega }_i^2{\xi }_i^2\text{\hspace{1em}(5.2.1.3)}$$

这就是弦的势能。

5.2.2 弦的动能

对于弦振动，其纵向位移$u$没有横向位移$v$显著，当为小扰动的时，在平衡状态点将它解耦，则动能可表示为：

$$K=\frac{1}{2}{\int }_0^{l_0}m(\frac{\partial v}{\partial t}{)}^2\mathrm{d}x$$

代入(3.2.4)得：

$$K=\frac{1}{2}{\int }_0^{l}m(\sum _{i=1}^{\infty }{\varphi }_i\dot{\xi }{)}^2\mathrm{d}x$$

和势能类似，求和平方简化为双重求和：

$$K=\frac{1}{2}{\int }_0^l\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\varphi }_i{\dot{\xi }}_i{\varphi }_j{\dot{\xi }}_{j}m(x)\mathrm{d}x=\frac{1}{2}\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\dot{\xi }}_i{\dot{\xi }}_j{\int }_0^{l}m(x){\varphi }_i{\varphi }_j\mathrm{d}x$$

利用正交性，即结合$(3.3.3)$、$(3.3.4)$得：

$$K=\frac{1}{2}\sum _{i=1}^{\infty }{M}_i{\dot{\xi }}_i^2\text{\hspace{1em}(5.2.2.1)}$$

这就是弦得动能。

5.2.3 弦的广义力

设弦上有分布载荷$f(x,t)$，则其虚功为：

$$\overline{\delta W}={\int }_0^{l_0}f(x,t)\delta v(x,t)\mathrm{d}x$$

其中虚位移$\delta v(x,t)$可写作广义坐标的形式：

$$\delta v(x,t)=\sum _{i=1}^{\infty }{\varphi }_i(x)\delta {\xi }_i(t)$$

于是虚功表达式为：

$$\overline{\delta W}={\int }_0^{l_0}\sum _{i=1}^{\infty }f(x,t){\varphi }_i(x)\delta {\xi }_i(t)\mathrm{d}x=\sum _{i=1}^{\infty }\delta {\xi }_i(t){\int }_0^{l_0}f(x,t){\varphi }_i(x)\mathrm{d}x$$

广义力和真实力按照虚功原理等效：

$$\sum _{i=1}^{\infty }\delta {\xi }_i(t){\Xi }_i(t)=\overline{\delta W}$$

于是，广义力为：

$${\Xi }_i(t)={\int }_0^{l_0}f(x,t){\varphi }_i(x)\mathrm{d}x\text{\hspace{1em}(5.2.3.1)}$$

如果弦上$x=x_c$处加载了集中力$F_c(t)$，则引入狄拉克函数$\delta (x-x_c)$即可。（注意：狄拉克函数的$\delta$是函数符号与虚位移无关。 此外，有关狄拉克函数的详细介绍可以看这里。）这时，其等效分布载荷为：

$$f(x,t)=F_c(t)\delta (x-x_c)$$

代入广义力公式：

$$\begin{array}{rl}{\Xi }_i(t)& ={\int }_0^{l_0}{F}_c(t)\delta (x-x_c){\varphi }_i(x)\mathrm{d}x\\ & =F_c(t){\int }_0^{l_0}\delta (x-x_c){\varphi }_i(x)\mathrm{d}x\\ & =f_c(t){\varphi }_i(x_c)\\ & =F_c(t)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x_c}{l})\end{array}\text{\hspace{1em}(5.2.3.2)}$$

其中：

5.2.4 广义运动方程的推导

注意到广义动能$(5.2.2.1)$仅为广义坐标变化率的函数，广义势能$(5.2.1.3)$仅为广义坐标的函数。所以拉格朗日方程可写作：

$$\frac{\mathrm{d}}{\mathrm{d}t}(\frac{\partial K}{\partial {\dot{\xi }}_i})+\frac{\partial P}{\partial {\xi }_i}={\Xi }_i$$

代入广义动能$(5.2.2.1)$、广义势能$(5.2.1.3)$得：

$$M_i({\ddot{\xi }}_i+{\omega }_i^2{\xi }_i)={\Xi }_i\text{\hspace{1em}(5.2.4.1)}$$

这就是广义运动方程。该方程也适用于非自由振动。（书中没有证明）

5.3 广义运动方程求解实例

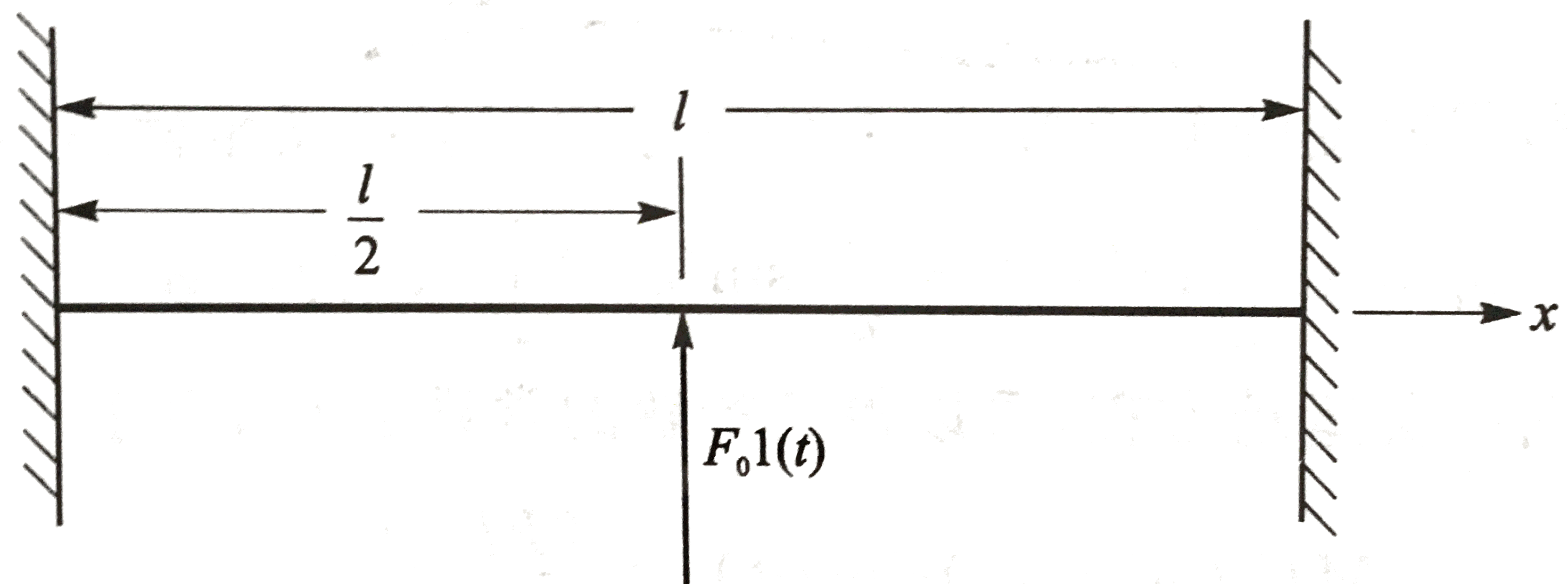
如图所示，幅值为$F_0$的集中阶跃函数的力作用在弦的中点处。

阶跃函数的定义为：

$$1(t)=\{\begin{array}{ll}0& (t<0)\\ 1& (t⩽0)\end{array}$$

弦的初始振型为：

$$v(x,0)=h\mathrm{s}\mathrm{i}\mathrm{n}(\frac{4\pi x}{l})$$

且初始速度为零。
求其响应。

解：

广义力：

$$\begin{array}{rl}{\Xi }_i& ={\int }_0^l{F}_{0}1(t)\delta (x-\frac{l}{2}){\varphi }_i(x)\mathrm{d}x\\ & =F_{0}1(t){\varphi }_i(\frac{l}{2})\\ & =F_{0}1(t)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi }{2})\end{array}$$

其中

$$\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi }{2})=\{\begin{array}{ll}0& (i为偶数)\\ (-1{)}^{\frac{i-1}{2}}& (i为奇数)\end{array}$$

代入广义运动方程$(5.2.4.1)$：

$$M_i({\ddot{\xi }}_i+{\omega }_i^2{\xi }_i)=\{\begin{array}{ll}0& (i为偶数)\\ F_{0}1(t)(-1{)}^{\frac{i-1}{2}}& (i为奇数)\end{array}$$

其通解为：

$${\xi }_i=\{\begin{array}{ll}{A}_i\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}t)+B_i\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)& (i为偶数)\\ A_i\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{i}t)+B_i\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)+C_i& (i为奇数)\end{array}\text{\hspace{1em}(5.3.1)}$$

其中：

$${\omega }_i=\frac{i\pi }{l}\sqrt{\frac{T}{m}}$$

下面处理初始条件：

弦具有初始振型：

$$\begin{array}{rl}v(x,0)& =\sum _{i=1}^{\infty }{\xi }_i(0){\varphi }_i(x)\\ & =\sum _{i=2,4,\cdots }^{\infty }{B}_i\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})+\sum _{i=1,3,\cdots }^{\infty }(B_i+C_i)\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\\ & =h\mathrm{s}\mathrm{i}\mathrm{n}(\frac{4\pi x}{l})\end{array}$$

将等式乘以$\mathrm{s}\mathrm{i}\mathrm{n}(j\pi x/l)\mathrm{d}x$，并沿弦长积分得：

$$\begin{array}{rl}h{\int }_0^l\mathrm{s}\mathrm{i}\mathrm{n}(\frac{4\pi x}{l})\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x=& \sum _{i=2,4,\cdots }^{\infty }{B}_i{\int }_0^l\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x+\\ & \sum _{i=1,3,\cdots }^{\infty }(B_i+C_i){\int }_0^l\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})\mathrm{s}\mathrm{i}\mathrm{n}(\frac{j\pi x}{l})\mathrm{d}x\end{array}$$

利用正弦函数得正交性得：

$$\begin{array}{cc}{B}_4=h& \\ B_i=0& (i为偶数，且i\ne 4)\\ B_i=-C_i& (i为奇数)\end{array}\}\text{\hspace{1em}(5.3.2)}$$

另外，初始速度为零：

$$\frac{\partial v}{\partial t}(x,0)=\sum _{i=1}^{\infty }{\dot{\xi }}_i(0){\varphi }_i(x)=\sum _{i=1}^{\infty }{\omega }_i{A}_i\mathrm{s}\mathrm{i}\mathrm{n}(\frac{i\pi x}{l})=0$$

将上式乘以$\mathrm{s}\mathrm{i}\mathrm{n}(j\pi x/l)\mathrm{d}x$并沿弦长积分。同样利用正弦函数的正交性得：

$$A_i=0\text{\hspace{1em}(5.3.3)}$$

将$(5.3.2)$和$(5.3.3)$代入$(5.3.1)$得：

$${\xi }_i=\{\begin{array}{ll}0& (i为偶数，且i\ne 0)\\ h\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)& (i=4)\\ C_i& (i为奇数)\end{array}$$

将${\xi }_i=C_i(i为奇数)$代入广义运动方程$(5.2.4.1)$：

$$M_i{C}_i{\omega }_i^2=F_0(-1{)}^{\frac{i-1}{2}}$$

对于均匀弦代入$(3.3.5)$第二式得：

$$C_i=\frac{2l{F}_0(-1{)}^{\frac{i-1}{2}}}{T(i\pi {)}^2}$$

则广义运动方程的解可以写成：

$${\xi }_i=\{\begin{array}{ll}0& (i为偶数，且i\ne 0)\\ h\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{i}t)& (i=4)\\ \frac{2l{F}_0(-1{)}^{\frac{i-1}{2}}}{T(i\pi {)}^2}& (i为奇数)\end{array}$$