多元回归
理论
- 当有p个自变量时,多元线性回归理论模型是
- 要进行回归分析,首先要构造矩阵X,矩阵X第一列都是1,用于求出上述式子中的b1。剩余的自变量,每个自变量的观测值排成一列。
- 返回的 b 是一个数组,即
先画出散点图判断是否具有线性关系
x1 = [3.5,5.3,5.1,5.8,4.2,6.0,6.8,5.5,3.1,7.2,4.5,4.9,8.0,6.5,6.5,3.7,6.2,7.0,4.0,4.5,5.9,5.6,4.8,3.9];
x2 = [9,20,18,33,31,13,25,30,5,47,25,11,23,35,39,21,7,40,35,23,33,27,34,15];
x3 = [6.1 6.4,7.4,6.7,7.5,5.9,6.0,4.0,5.8,8.3,5.0,6.4,7.6,7.0,5.0,4.0,5.5,7.0,6.0,3.5,4.9,4.3,8.0,5.0];
Y = [33.2,40.3,38.7,46.8,41.4,37.5,39.0,40.7,30.1,52.9,38.2,31.8,43.3,44.1,42.5,33.6,34.2,48.0,38.0,35.9,40.4,36.8,45.2,35.1];
n = size(x1,2);
m = 3;
subplot(1,3,1),plot(x1,Y,'g*'),
subplot(1,3,2),plot(x2,Y,'k+'),
subplot(1,3,3),plot(x3,Y,'ro'),
得到图像如下:
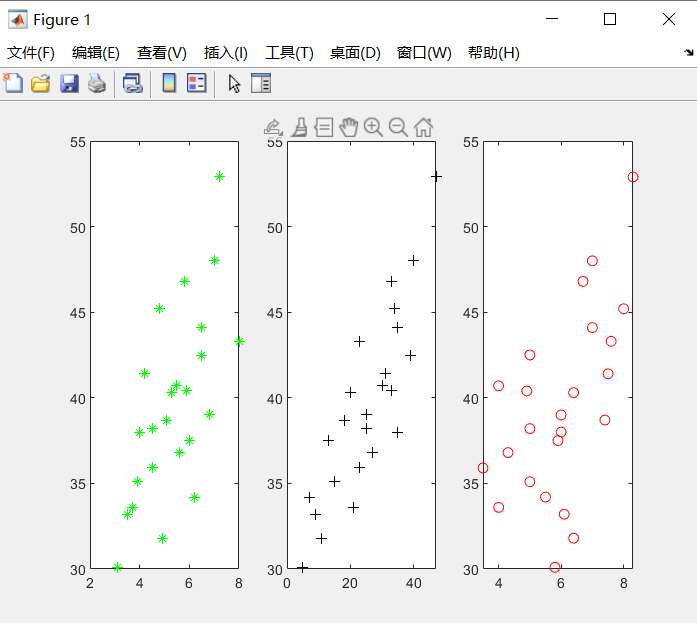
subplot函数的用法

在一元线性回归里面我们讲到了regress函数,在这里多元回归,我们同样使用regress函数。
regress函数的用法
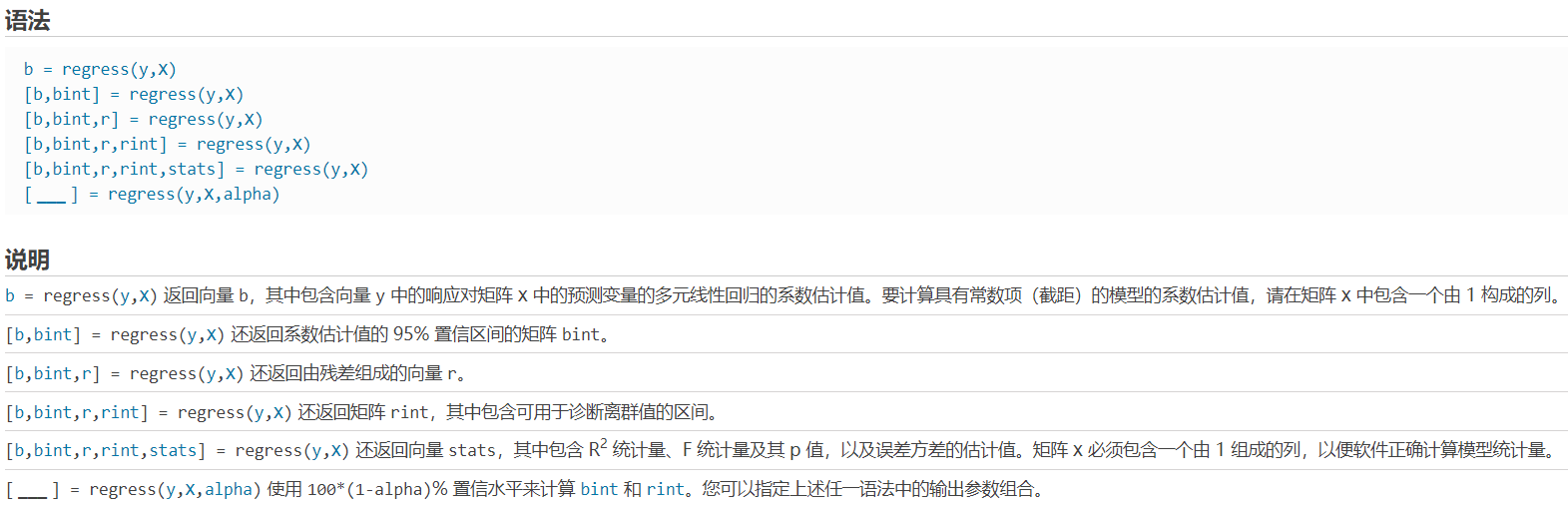
X = [ones(n,1),x1',x2',x3']; %这个地方全1的列向量是必须存在的
[b,bint,r,rint,s] = regress(Y',X,0.05); %0.05代表95%的置信区间
输出结果如图:
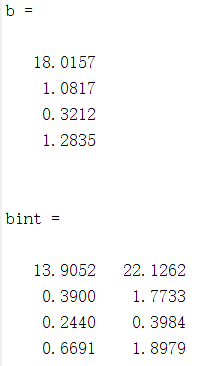

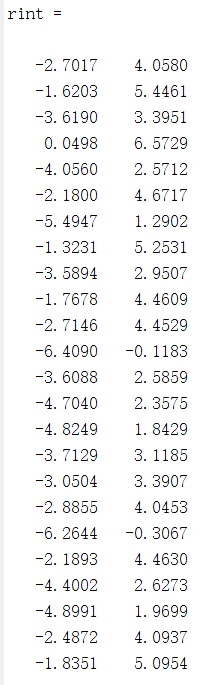

- b:回归系数
- bint:回归置信区间
- s :统计变量包括:相关系数的平方R2,假设检验统计量F,F对应的概率p,F对应的概率s2。
根据上述结果,可以得到回归方程:
y = 18.0157+1.0817x1+0.3212x2+1.2835x3
结果检验
- 回归系数置信区间 不包含零点表示模型较好
- 残差 在零点附近表示模型较好
- s 返回四个值,相关系数平方 ,假设检验统计量 , 对应的概率
- 相关系数 :R大表明线性相关性较强
- F 检验:应满足 ,其中 分别为设置的置信区间、因变量个数、因变量数据的个数。
- p:应满足
- :应越小越好,主要在建模改进时作为参考数据。
结果分析

本文章使用limfx的vscode插件快速发布