MATLAB 解微分方程组

解单一微分方程组

S=dsolve(eqn,cond)

• eqn是微分方程等式，其中微分用diff函数表示，cond是确定微分方程不定系数的条件。 确定初始条件时要设置一个新变量：

\[ Dy=diff(y,x)\quad Dy(0)==1 \]

• 如果没有 cond 则为解中含有不定系数C。

• 注意，定义变量的时候要用 () 将自变量括起来。

举例

求解微分方程：

\[ y'''-3y''+3y'-y=-1 \]

初始条件

\[ y''(0)=y'(0)=1,\quad y(0)=2 \]

syms y(x)
eqn = diff(y, x, 3) - 3 * diff(y, x, 2) + 3 * diff(y, x) - y == -1;
Dy = diff(y, x);
D2y = diff(y, x, 2);
conds = [Dy(0) == 1, D2y(0) == 1, y(0) == 2];
sol = dsolve(eqn, conds);

解微分方程组

Y=dsolve(eqns,cond)

• Y、eqn的形式和solve中的Y相同（参见解方程组部分）

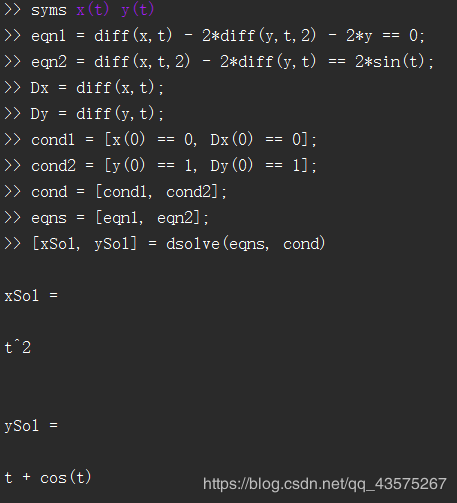
举例

\[ \left\{ \begin{aligned} x'-2y''-2y=0,\quad x(0)=x'(0)=0\\ x''-2y'=2sin(t),\quad y(0)=y'(0)=1 \end{aligned} \right. \]

---

本文章使用limfx的vsocde插件快速发布