MATLAB 积分计算与积分变换
积分计算
命令 | 说明 |
|---|---|
int(f) | 计算函数 f 的不定积分 |
int(f,x) | 计算函数 f 关于自变量x的不定积分 |
int(f,a,b) | 计算函数 f 在区间 [a,b] 上的定积分 |
int(f,x,a,b) | 计算函数 f 关于自变量x在区间 [a,b] 上定积分 |
MATLAB中的函数只能计算一次积分,但是上限和下限可以含未知变量。要 计算二重积分和三重积分就要引用两次、三次 int。而计算在一定区域内的二重积分和三重积分要先手动化成带积分限的形式,例如:
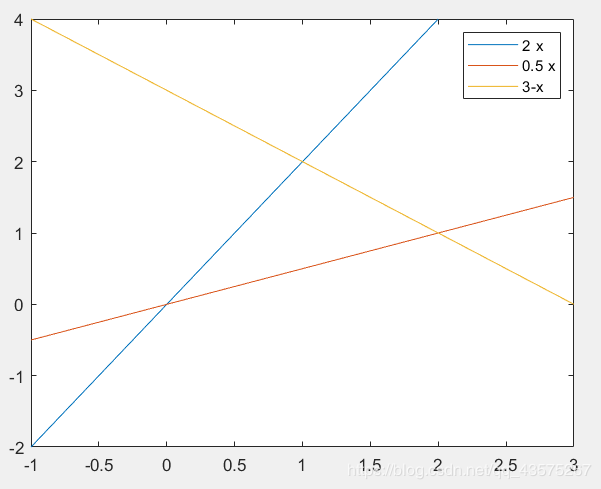
\[ \iint_D x \ dxdy \quad D: y=2x\quad y=0.5x \quad y=3-x \]
先给出定义域并解出交点坐标:
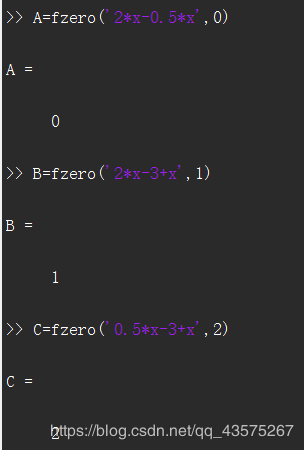
如图给出了图形的定义域,下求三个交点的横坐标。用函数 fzero 调用方法参见非线性方程求解。
由此可知所求的积分可以化为:
\[ \int_0^1dx \int_{0.5x}^{2x} x \ dy+ \int_1^2 dx \int_{0.5x}^{3-x} \ x \ dy \]
积分变换
傅里叶变换
命令 | 说明 |
|---|---|
F=fourier(f) | 求 f 关于 x 的傅里叶积分变换,返回自变量为 w |
F=fourier(f,v) | 返回的函数以 v 为自变量 |
F=fourier(f,u,v) | 返回的函数以 v 为自变量,函数 f 自变量为 u |
f=ifourier(F) | 求 F 关于 w 的傅里叶积分逆变换,返回自变量为 x |
f=ifourier(F,v) | 返回的函数以 v 为自变量 |
f=ifourier(F,u,v) | 返回的函数以 v 为自变量,函数 F 自变量为 u |
拉普拉斯变换
命令 | 说明 |
|---|---|
F=laplace(f) | 求 f 关于 t 的拉普拉斯变换,返回自变量为 s |
F=laplace(f,v) | 返回的函数以 v 为自变量 |
F=laplace(f,u,v) | 返回的函数以 v 为自变量,函数 f 自变量为 u |
f=ilaplace(F) | 求 F 关于 s 的拉普拉斯积分逆变换,返回自变量为 t |
f=ilaplace(F,v) | 返回的函数以 v 为自变量 |
f=ilaplace(F,u,v) | 返回的函数以 v 为自变量,函数 F 自变量为 u |
本文章使用limfx的vsocde插件快速发布