粘性流体力学期末总结（一）

粘性流体力学期末总结（一）

Chapter 1. Introduction

1.2 流体力学和粘性

流体的特点：

静态时无切应力；
可采用欧拉法坐标系；
流体被流体包围。

粘性：当流体受到外界的剪切力作用的时候，它会不断地变形下去，在这种连续的剪切变形作用下的流体内部会产生剪切力，这种性质称为流体的粘性。
粘性力（动态）不同于附着力（静态）。

1.3 湍流

雷诺数：

Re = \frac{\rho VL}{\mu} = \frac{VL}{\nu} = \frac{惯性力}{粘性力}

形成湍流的条件：雷诺数足够高，扰动足够大。

1.4 流动中的粘性效应

阻力危机：
随着雷诺数增大，层流转为湍流，气动分离点后移。压差阻力减小，导致阻力系数突然地减小。

Chapter 2. Equations of Flow

2.1 流动运动学

流体中点的运动：

\vec{V} = \vec{i}u+\vec{j}v+\vec{k}w\\
\vec{a} = \vec{i}\frac{\mathrm{d}u}{\mathrm{d}t} + \vec{j}\frac{\mathrm{d}v}{\mathrm{d}t} + \vec{i}\frac{\mathrm{d}w}{\mathrm{d}t}

在欧拉法坐标系下，流体运动被描述为运动场。在运动场中，速度被视为空间和时间的多元函数。则：

\frac{\mathrm{d}u}{\mathrm{d}t} = \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial u}{\partial y}\frac{\partial y}{\partial t} + \frac{\partial u}{\partial z}\frac{\partial z}{\partial t} = \frac{\partial u}{\partial t} + \frac{\partial u}{\partial x}u + \frac{\partial u}{\partial y}v + \frac{\partial u}{\partial z}w\\
\vec{a} = \frac{\partial \vec{V}}{\partial t} + (\vec{V}\cdot\bigtriangledown)\vec{V}\\
a_i = \frac{\partial u_i}{\partial t} + u_j\bigtriangledown_ju_i = \frac{\partial u_i}{\partial t} + u_j\frac{\partial u_i}{\partial x_j}

其中被称为当地加速度，被称为对流加速度。
上式具有普遍意义：对于流动中一个参数，有：

\frac{\mathrm{d}\Phi}{\mathrm{d}t}= \frac{\partial \Phi}{\partial t} + u_j\bigtriangledown_j\Phi = \frac{\partial \Phi}{\partial t} + (\vec{V}\cdot\bigtriangledown)\Phi

这被称为物质导数。

流体单元的运动（赫姆霍兹速度分解定理）
一般运动=平动+转动+变形(可以由对速度场泰勒一阶展开得到)

(u_j)_A = (u_j)_P + \frac{\partial u_j}{\partial x_i}\delta x_i\\
\frac{\partial u_j}{\partial x_i} = 
\begin{bmatrix}
   \frac{\partial u}{\partial x} && \frac{\partial u}{\partial y} && \frac{\partial u}{\partial z}\\
   \frac{\partial v}{\partial x} && \frac{\partial v}{\partial y} && \frac{\partial v}{\partial z}\\
   \frac{\partial w}{\partial x} && \frac{\partial w}{\partial y} && \frac{\partial w}{\partial z}
\end{bmatrix}
\\
=\frac{1}{2}(J+J^T)+\frac{1}{2}(J-J^T)=\\
\begin{bmatrix}
   \frac{\partial u}{\partial x} & \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}) & \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\\
   \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}) & \frac{\partial v}{\partial y} & \frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\\
   \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}) & \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}) & \frac{\partial w}{\partial z}
\end{bmatrix}
+
\begin{bmatrix}
   0 & \frac{1}{2}(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}) & \frac{1}{2}(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})\\
   -\frac{1}{2}(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}) & 0 & \frac{1}{2}(\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y})\\
   -\frac{1}{2}(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}) & -\frac{1}{2}(\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y}) & 0
\end{bmatrix}
\\=变形+转动=\\
\begin{bmatrix}
   \frac{\partial u}{\partial x} & 0 & 0\\
   0 & \frac{\partial v}{\partial y} & 0\\
   0 & 0 & \frac{\partial w}{\partial z}
\end{bmatrix}
+
\begin{bmatrix}
   0 & \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}) & \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})\\
   \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}) & 0 & \frac{1}{2}(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y})\\
   \frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}) & \frac{1}{2}(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}) & 0
\end{bmatrix}
+
\begin{bmatrix}
   0 & \frac{1}{2}(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}) & \frac{1}{2}(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x})\\
   -\frac{1}{2}(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}) & 0 & \frac{1}{2}(\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y})\\
   -\frac{1}{2}(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}) & -\frac{1}{2}(\frac{\partial v}{\partial z}-\frac{\partial w}{\partial y}) & 0
\end{bmatrix}
\\=线变形+角变形+转动

其中：
正应变速率：

\begin{aligned}
   \epsilon'_x &= \frac{\partial u}{\partial x}\\
   \epsilon'_y &= \frac{\partial v}{\partial y}\\
   \epsilon'_z &= \frac{\partial w}{\partial z}
\end{aligned}

角应变速率：

\epsilon'_{ij} = \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}

应变速率：

s_{ij} = \frac{1}{2}(\bigtriangledown_iu_j+\bigtriangledown_ju_i)

角速度：

\omega_i = \epsilon_{ijk}\bigtriangledown_ju_k\\
(\epsilon_{ijk}为里奇函数，不是应变)

2.2 流体单元上的应力

体力+面力=

\vec{F}_{body}=\vec{f}_b\rho\mathrm{d}x\mathrm{d}y\mathrm{d}z\\
\vec{F}_{surface} = (\frac{\partial \vec{\Gamma}_x}{\partial x} + \frac{\partial \vec{\Gamma}_y}{\partial y} + \frac{\partial \vec{\Gamma}_z}{\partial z})\mathrm{d}x\mathrm{d}y\mathrm{d}z\\
\Gamma_{ij} = [\tau_{ij}] =
\begin{bmatrix}
   \tau_{xx}&\tau_{xy}&\tau_{xz}\\
   \tau_{yx}&\tau_{yy}&\tau_{yz}\\
   \tau_{zx}&\tau_{zy}&\tau_{zz}
\end{bmatrix}

2.4 牛顿流体的本构关系

牛顿内摩擦定律：

\tau_{yx}=\mu\frac{\partial u}{\partial y}

求，为应变率。

斯托克斯假设：

连续，且
各向同性
也适用于流体静止时（）

由以上假设条件可以得：

\tau_{ij} = 2\mu s_{ij}-[\lambda(\bigtriangledown_ku_k)-p]\delta_{ij}\\
(\bigtriangledown_ku_k=\frac{\partial u_k}{\partial x_k} = \mathrm{div}(u_i)——散度)

斯托克斯假设，则

\tau_{ij} = 2\mu s_{ij} - \frac{2}{3}\mu (\bigtriangledown_ku_k)\delta_{ij} - p\delta_{ij}\\
\tau_{ij}=\left\{
\begin{aligned}
   &\mu(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}) &(i\neq j) 剪应力\\
   &2\mu\frac{\partial u_i}{\partial x_j}-\frac{2}{3}\mu \frac{\partial u_k}{\partial x_k} - p &(i=j) 正应力
\end{aligned}
\right.

流体应力=粘性项+压缩项+外部压力项

2.5 连续性方程

2.5.1 连续性方程积分形式

由质量守恒：
对于拉格朗日法，研究流体微团质量不随时间改变：

\frac{\mathrm{d}m_{sys}}{\mathrm{d}t}=\frac{\mathrm{d}}{\mathrm{d}t} \iiint \rho\mathrm{d}B = 0

对于欧拉法，流出控制体的质量等于控制体内减少的质量：

\frac{\partial}{\partial t}\iiint_{CV}\rho\mathrm{d}B + \oiint_{CS}\rho(\vec{V}\cdot\vec{n})\mathrm{d}A = 0

2.5.2 连续性方程的微分形式

由高斯散度定理：

\oiint_{CS}\rho(\vec{V}\cdot\vec{n})\mathrm{d}A =\iiint_{CV}\bigtriangledown\cdot(\rho\vec{V}){d}B

于是

\frac{\partial}{\partial t}\iiint_{CV}\rho\mathrm{d}B + \iiint_{CV}\bigtriangledown\cdot(\rho\vec{V}){d}B = 0\\
\iiint_{CV}[\frac{\partial \rho}{\partial t}+\bigtriangledown\cdot(\rho\vec{V})]{d}B = 0

得到连续性方程的微分形式:

\frac{\partial \rho}{\partial t}+\bigtriangledown\cdot(\rho\vec{V})=0

由于：

\bigtriangledown\cdot(\rho\vec{V}) = (\vec{V}\cdot\bigtriangledown)\rho + \rho(\bigtriangledown\cdot\vec{V})\\
\frac{\mathrm{d}\rho}{\mathrm{d}t} = \frac{\partial \rho}{\partial t} + (\vec{V}\cdot\bigtriangledown)\rho

得另一种形式的连续性方程：

\frac{\mathrm{d}\rho}{\mathrm{d}t}+\rho(\bigtriangledown\cdot\vec{V}) = 0

可以看出对于不可压缩流体（），有散度为零（）

2.6 动量方程

由牛顿第二定律可以推得：拉格朗日法形式动量方程：

\sum\vec{F}_{sys} = \frac{\mathrm{d}}{\mathrm{d}t}\iiint_{sys}\vec{V}\rho\mathrm{d}B

欧拉法形式的动量方程：

\sum\vec{F}_{CV} = \frac{\partial}{\partial t}\iiint_{CV}\vec{V}\rho\mathrm{d}B + \oiint_{CS}\vec{V}\rho(\vec{V}\cdot\vec{n})\mathrm{d}A

微分形式：

\frac{\partial u_i}{\partial t} + u_j\bigtriangledown_j u_i = f_i + \frac{1}{\rho}\bigtriangledown_j\tau_{ji}

可带入本构关系：

\tau_{ij}=2\mu s_{ij} - \frac{2}{3}\mu\bigtriangledown_k(u_k)\delta_{ij} - p\delta_{ij}

得：

\rho\frac{\partial u_i}{\partial t} + \rho u_j\bigtriangledown_ju_i = \rho f_i - \bigtriangledown_ip + \mu \bigtriangledown_j(\bigtriangledown_j u_i) + \frac{1}{3}\mu\bigtriangledown_i(\bigtriangledown_ju_j)

动量改变率（-惯性力）=体力+压力+粘性力

2.7 能量方程

2.7.1 原始能量方程

可由能量守恒得：

\rho\frac{\mathrm{d}(\hat{u}+V^2/2)}{\mathrm{d}t} = \rho\vec{f}\cdot\vec{V} + \bigtriangledown\cdot(\vec{V}\cdot\tau) + \bigtriangledown\cdot(\lambda\bigtriangledown T) + \rho\dot{q}_{rad}

其张量形式：

\rho\frac{\mathrm{d}(\hat{u}+u_iu_i/2)}{\mathrm{d}t} = \rho f_iu_i + \bigtriangledown_i(\tau_{ij}u_j) + \bigtriangledown_i(\lambda\bigtriangledown_i T) + \rho\dot{q}_{rad}

等式右边四项分别代表：体力功、面力功、热传导、热辐射

2.7.2 能量方程的拆分

对动量方程两边同乘以得：

\frac{\mathrm{d}(u_iu_i/2)}{\mathrm{d}t} = f_iu_i + \frac{1}{\rho}\bigtriangledown_j(\tau_{ji})u_i

上式表示动能与功的关系（动能=体力做功+面力在微团移动做的功）。

将能量方程改写：

\rho\frac{\mathrm{d}(u_iu_i/2)}{\mathrm{d}t} + \rho\frac{\mathrm{d}\hat{u}}{\mathrm{d}t} = \rho f_iu_i + \bigtriangledown_j(\tau_{ji})u_i + \tau_{ji}\bigtriangledown_i(u_j) + \bigtriangledown_i(\lambda\bigtriangledown_i T) + \rho\dot{q}_{rad}

式中代入本构关系可写作：

\tau_{ji}\bigtriangledown_i(u_j) = (2\mu s_{ji} - \frac{2}{3}\mu (\bigtriangledown_ku_k)\delta_{ji} - p\delta_{ji})\bigtriangledown_iu_j= -p\bigtriangledown_ju_j - \frac{2}{3}\mu(\bigtriangledown_ku_k)(\bigtriangledown_ju_j) + \mu(\bigtriangledown_ju_i)(\bigtriangledown_iu_j) + \mu(\bigtriangledown_iu_j)(\bigtriangledown_iu_j)

第二项为粘性力正应力做的体积功，较小一般忽略，于是可写作：

\tau_{ji}\bigtriangledown_i(u_j) = -p\bigtriangledown_iu_i + \Phi_{\nu}

其中：
为体积功，可逆；
表示由于粘性力在线变形和角变形上做的功，不可逆，为耗散项。

能量方程可拆分为：

\rho\frac{\mathrm{d}(u_iu_i/2)}{\mathrm{d}t} = \rho f_iu_i + \bigtriangledown_j(\tau_{ji})u_i —— 动能方程\\
\rho\frac{\mathrm{d}\hat{u}}{\mathrm{d}t} = -p\bigtriangledown_iu_i + \Phi_{\nu} + \bigtriangledown_i(\lambda\bigtriangledown_iT) + \rho\dot{q}_{rad} —— 内能方程

2.7.3 热力学相关量提取

根据提取的内能方程。

由焓的定义得：

\rho\frac{\mathrm{d}h}{\mathrm{d}t} = \frac{\mathrm{d}p}{\mathrm{d}t} + \Phi_{\nu} + \bigtriangledown_i(\lambda\bigtriangledown_iT) + \rho\dot{q}_{rad} —— 焓方程

由熵的定义得：

\rho T\frac{\mathrm{d}s}{\mathrm{d}t} = \Phi_{\nu} + \bigtriangledown_i(\lambda\bigtriangledown_iT) + \rho\dot{q}_{rad} —— 熵方程

由总焓的定义得：

\rho\frac{\mathrm{d}(h+u_iu_i/2)}{\mathrm{d}t} = \frac{\partial p}{\partial t} + \rho f_iu_i + \Phi_{\nu} + \bigtriangledown_i(\lambda\bigtriangledown_iT) + \rho\dot{q}_{rad} —— 总焓方程

可以看出，不计体积功，非定常压力是等熵地增加总焓的唯一方式。

2.7.4 轴功

轴功的表达式为：

-\dot{w}_s = \int(\frac{1}{\rho}\frac{\partial p}{\partial t} + u_j\bigtriangledown_i\tau_{\nu,ij} + \frac{1}{\rho}\Phi_{\nu})\mathrm{d}t\\
\tau_{\nu,ij}为除去正压力的表面力，即粘性力。

轴功由三个部分构成：非定常压力做工，粘性力作移动功，粘性力做变形功。

2.7.5 流动功和体积功

流体运动中，克服前方压力推进做负功，推进后方流体以压力做正功。记二者之差为流动功

W_{flow} = W_2+W_1 = p_2A_2(\delta x)_2 - p_1A_1(\delta x)_1

同时微分形式可写作：

\mathrm{d}(pv) = p\mathrm{d}v + v\mathrm{d}p

流动功=体积功+耗散功

2.9 无量纲化和无量纲数

雷诺数：

Re = \frac{\rho VL}{\mu}=\frac{对流惯性力}{粘性力}

判定层流湍流；

马赫数：

Ma = \frac{V}{a}=\frac{惯性力}{弹性力}

高速流动中压缩性；

斯克劳哈尔数：

St = \frac{fL}{V}=\frac{局部惯性力（非定常惯性力）}{对流惯性力（定常惯性力）}

描述振荡程度；

弗劳德数：
```
Fr = \frac{V}{\sqrt{gL}}=\frac{对流惯性力}{重力}
```
用于在处理重力场内液体的自由表面相关的运动。

欧拉数：

Eu = \frac{p}{\rho V^2}=\frac{压力}{对流惯性力}

常用于势流法分析；

其他：

k = \frac{c_p}{c_v}\\
Pr = \frac{\mu c_p}{k}\\
Nu = \frac{hL}{k}

2.10 涡和涡量

流体微团角速度

\Omega = \frac{V_\theta}{r}\\
\Omega_i = \frac{1}{2}\epsilon_{ijk}\bigtriangledown_ju_k

涡量

\vec{\omega} = \bigtriangledown \times \vec{V}\\
\omega_i = \epsilon_{ijk}\bigtriangledown_ju_k

无粘流体涡量守恒 看起来旋转，不一定有涡量；有涡量，不一定看起来有旋转。

Chapter 3. Solutions of Flow

3.1 N-S方程组的解

质量：
动量：
能量：
状态方程：或

3.1.1 定常平行流动

3.1.1.1 库埃特流动

二维、定常、不可压缩、无体力
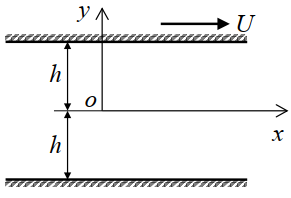
库埃特流动图

连续性方程：
由不可压得即：

\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0

又，得：

\frac{\partial u}{\partial x}=0

则

\begin{aligned}
   u&=u(y)\\
   v&=0
\end{aligned}

动量方程：
将上式代入动量方程，化简得

\begin{aligned}
   \frac{\partial p}{\partial x} &= \mu\frac{\partial^2 u}{\partial y^2}\\
   \frac{\partial p}{\partial y} &= 0
\end{aligned}

又：

\frac{\mathrm{d}p}{\mathrm{d}x}=\mu\frac{\mathrm{d}^2u}{\mathrm{d}y^2}=\mathrm{const}

（上式中左边是一个只与有关的函数，右边是一个只与有关的函数，二者恒相等，则二者同为常数）

同时有边界条件：

u=
\left\{
   \begin{aligned}
      & 0 &(y=-h)\\
      & U &(y=h)
   \end{aligned}
\right.

解得：

u=\frac{U}{2}(1+\frac{y}{h}) - \frac{h^2}{2\mu}\frac{\mathrm{d}p}{\mathrm{d}x}[1-(\frac{y}{h})^2]

，顺压力梯度
，逆压力梯度

若，

u=\frac{U}{2}(1+\frac{y}{h})

速度成线性关系：
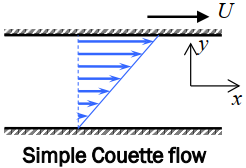
简单库埃特流动

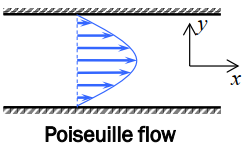
若，

u=-\frac{h^2}{2\mu}\frac{\mathrm{d}p}{\mathrm{d}x}[1-(\frac{y}{h})^2]

速度呈对称抛物线分布：
泊肃叶流动

切应力沿方向呈线性关系：

\tau_{xy}=\tau_{yx}=\mu(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})=\mu\frac{\mathrm{d}u}{\mathrm{d}y}=\mu\frac{U}{2h}+\frac{\mathrm{d}p}{\mathrm{d}x}y

3.1.1.2 哈根-泊肃叶流动

柱坐标系的库埃特流动：
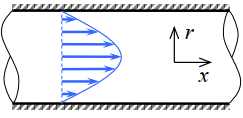
哈根-泊肃叶流动

方向的动量方程：

u_r\frac{\partial u_x}{\partial r}+\frac{u_\theta}{r}\frac{\partial u_x}{\partial \theta}+u_x\frac{\partial u_x}{\partial x} \\
= -\frac{1}{\rho}\frac{\partial p}{\partial x}+\frac{\mu}{\rho}(\frac{\partial^2 u_x}{\partial r^2}+\frac{1}{r}\frac{\partial u_x}{\partial r}+\frac{1}{r^2}\frac{\partial^2 u_x}{\partial \theta^2}+\frac{\partial^2 u_x}{\partial x^2})

与普通库埃特流动一样有：

\frac{\partial u_x}{\partial r}=0\,\,\,\frac{\partial u_x}{\partial x}=0

流动是沿着圆柱中心线对称的:

\frac{\partial u_x}{\partial \theta}=0\,\,\,u_\theta=0\,\,\,u_r=0

可将动量方程化简为：

\mu(\frac{\mathrm{d}^2 u_x}{\mathrm{d}r^2}+\frac{1}{r}\frac{\mathrm{d}u_x}{\mathrm{d}r}) = \frac{\mathrm{d}p}{\mathrm{d}x}=\mathrm{const}

同时有边界条件：

\left\{
   \begin{aligned}
      &u=0\,\,\,&(r=R)\\
      &\mathrm{d}u/\mathrm{d}r=0\,\,\,&(r=0)
   \end{aligned}
\right.

解得：

u = \frac{1}{4\mu}\frac{\mathrm{d}p}{\mathrm{d}x}(R^2-r^2)

若令平均速度，计算得：

U = -\frac{1}{8\mu}\frac{\mathrm{d}p}{\mathrm{d}x}R^2 = u_\mathrm{max}/2

则流动速度函数可写作：

u = 2U[1-(\frac{r}{R})^2]

壁面剪切应力为：

\tau_w = \mu\frac{\mathrm{d}u}{\mathrm{d}r}\Big|_{r=R} = \frac{4\mu U}{R}

定义表面摩擦系数为：

C_\mathrm{f} = \frac{\tau_w}{\rho U^2/2}

结合上两式可得：

C_\mathrm{f} = \frac{16\mu}{\rho UD}=\frac{16}{Re}

3.2 边界层理论

Although frictional effects in slightly viscous fluid are indeed present, they are confined to a thin layer near the surface of the body, the rest of the flow can be considered inviscid. —— Prandtl 1904

粘性只在物体表面很薄的区域类有明显作用，其他区域可视为无粘。 这层区域被称为边界层。（这是一个工程近似理论，是把无粘理论运用到有粘情况的工程条件。）

3.2.1 普朗特边界层方程

按照普朗特的假设，可以构造下面的模型：
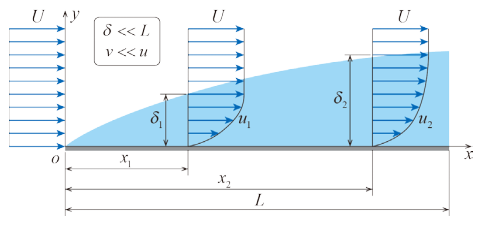
平板边界层
为边界层厚度，普朗特把它们定义为边界层内流场速度中流速达到来流速度的0.99倍的位置。

以二维、定常、不可压缩、无体力的情况为例：
动量方程：

\left\{
   \begin{aligned}
      u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \frac{\mu}{\rho}(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2})\\
      u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y} + \frac{\mu}{\rho}(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2})
   \end{aligned}
\right.

量纲分析：选择、和为参考量。

u \sim [U] \,\,,\,\, x \sim [L] \,\,,\,\, y \sim [\delta]

由于不可压缩，：

\frac{U}{L} + \frac{v}{\delta} = 0

得：

v \sim [\frac{U\delta}{L}]

将上述参考量代入动量方程各项中化简，注意有：

\delta << L

凡是带有项的都可以视为零。简化得：

\left\{
   \begin{aligned}
      &u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \frac{\mu}{\rho}\frac{\partial^2 u}{\partial y^2}\\
      &\frac{\partial p}{\partial y} = 0
   \end{aligned}
\right.

其中：
惯性力为
粘性力为
在边界层内，惯性力和粘性力应该相当：
则有：

\frac{\delta}{L} \sim \frac{1}{\sqrt{Re}}

由于，得：

Re >> 1

对于边界层以外流动，无粘：

U\frac{\partial U}{\partial x} + V\frac{\partial U}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x}

且有，则：

U\frac{\partial U}{\partial x} = -\frac{1}{\rho}\frac{\partial p}{\partial x}

代入到简化后的边界层内的动量方程：

u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = U\frac{\partial U}{\partial x} + \frac{\mu}{\rho}\frac{\partial^2 u}{\partial y^2}

运动粘度，且有边界条件，得普朗特边界层方程：

\left\{
   \begin{aligned}
      &u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = U\frac{\partial U}{\partial x} +\nu\frac{\partial^2 u}{\partial y^2}\\
      &u=v=0\,\,\,(y=0)\\
      &u\approx U(x)\,\,\,(y=\delta)\\
      &\delta << L\\
      &Re >> 1
   \end{aligned}
\right.

若把上面第一式移项：

-(u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y})+\nu\frac{\partial^2 u}{\partial y^2} = -U\frac{\partial U}{\partial x}

这就是：边界层内惯性力+粘性力=边界层外惯性力

3.2.2 布拉修斯解

\left\{
   \begin{aligned}
      &f=\sum_{n=0}^\infin(-\frac{1}{2})^n\frac{0.332^{n+1}C_n}{(3n+2)!}\eta^{(3n+2)}\\
      &f=\int u^*\mathrm{d}\eta\\
      &u^*=u/U\\
      &\eta=y/\sqrt{\frac{\mu x}{\rho U}}
   \end{aligned}
\right.

3.2.3 积分方法

3.2.3.1 排挤厚度

在壁面附近的流体受粘性影响而减速，同样的厚度内就会减少过去流过去一部分流体，质量守恒，流体会被向上排挤，处于边界层之外的主流就相应地抬起一个高度，这各高度就定义为边界层的排挤厚度（位移厚度），。（即：由于摩擦损失的自由流动的流量的厚度）
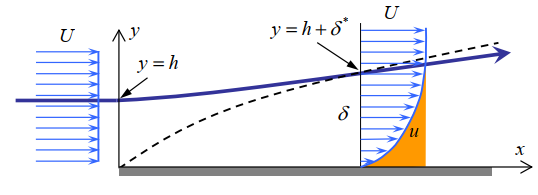
排挤边界层厚度
从壁面开始到边界层外界之间的总流量为：

\dot{m}_{real} = \int_0^\delta \rho ub\mathrm{d}y\\
（b为平板的展向厚度）

如果边界层内的流体没有被减速，同样的高度范围内应该通过的流量为：

\dot{m}_{ideal} = \rho Ub\delta

假设流体不可压，少通过的流量为：

\Delta\dot{m} = \dot{m}_{ideal}-\dot{m}_{real} = \rho b\int_0^\delta(U-u)\mathrm{d}y

边界层外流体被抬升了高度，则边界层内部厚度的区域内没有通过流体：

\Delta\dot{m} = \rho Ub\delta^*

对比两式得到排挤厚度的表达式：

\delta^* = \int_0^\delta(1-\frac{u}{U})\mathrm{d}y

更严格的，其表达式为：

\delta^* = \int_0^\infin(1-\frac{u}{U})\mathrm{d}y

3.2.3.2 动量损失厚度（）

动量损失厚度表示由于粘性损失了的自由流动的动量的折算为边界层外流速的厚度。

令为动能流量：

\Delta\dot{M} = \rho U\theta bU

同时有：

\Delta\dot{M} = \dot{M}_{ideal}-\dot{M}_{real} = \int_0^\delta\rho u\mathrm{d}y\cdot U-\int_0^\delta\rho u\mathrm{d}y\cdot u

对比得到：

\theta = \int_0^\delta\frac{u}{U}(1-\frac{u}{U})\mathrm{d}y

更严格的为：

\theta = \int_0^\infin\frac{u}{U}(1-\frac{u}{U})\mathrm{d}y

类似地，也有能量损失厚度：

\delta_3 = \int_0^\infin\frac{u}{U}(1-\frac{u^2}{U^2})\mathrm{d}y

3.2.3.3 边界层的积分关系式

将普朗特边界层方程沿积分：

\int_0^\delta(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}-U\frac{\partial U}{\partial x})\mathrm{d}y = \frac{\mu}{\rho}\int_0^\delta(\frac{\partial^2 u}{\partial y^2})\mathrm{d}y

右侧：

RHS=\frac{\mu}{\rho}\int_0^\delta(\frac{\partial^2 u}{\partial y^2})\mathrm{d}y= \frac{\mu}{\rho}[(\frac{\partial u}{\partial y})_{y=\delta}-(\frac{\partial u}{\partial y})_{y=0}]=-\frac{\tau_w}{\rho}

左侧;

LHS=-U^2\frac{\mathrm{d}\theta}{\mathrm{d}x}-U\theta(2+H)\frac{\mathrm{d}U}{\mathrm{d}x}\\
H=\frac{\delta^*}{\theta}（形状因子）

于是：

\frac{\mathrm{d}\theta}{\mathrm{d}x}+(2+H)\frac{\theta}{U}\frac{\mathrm{d}U}{\mathrm{d}x}=\frac{\tau_w}{\rho U^2}

这就是：冯·卡门边界层动量积分方程
由于表面摩擦系数为，上式也可写作：

\frac{\mathrm{d}\theta}{\mathrm{d}x}+(2+H)\frac{\theta}{U}\frac{\mathrm{d}U}{\mathrm{d}x}=\frac{C_f}{2}

可以利用此方程迭代求得流场:

假定流动为无粘，用势流法求出沿壁面的速度分布。
根据之前的前面求得的边界层内沿方向的速度分布，补充速度在边界层内沿方向的速度分布（比如假设为抛物线分布），并有牛顿内摩擦定律，代入冯·卡门动量积分方程，求得排挤厚度。
将用上面求出的排挤厚度修正壁面形状，再次用势流法求解速度分布。
重复，迭代。

3.3 边界层分离

边界层内流速减慢，甚至倒流，边界层增大，就像边界层离开了壁面一样，使普朗特假设不成立。

边界层分离得条件：粘性、逆压梯度。
边界层分离增加阻力：边界层分离，使分离区的总压耗散得更大，且产生回流（动压减小不明显），使得后部分得静压下降更快。造成前后压差增大，增大了压差阻力。
边界层分离造成损失增加：使分离流掺混，造成损失。
控制边界层分离：使速度剖面更加饱满、使层流转湍流、改善压力梯度。

Chapter 4. Turbulent Flow

4.2 均匀各向同性湍流理论

4.2.1 雷诺平均

高雷诺数下，流体会在时空中不规则。产生涡（eddy）。

雷诺平均：实际量=平均量+脉动量（）

将此式代入N-S方程中：

\frac{\mathrm{d}\overline{u_i}}{\mathrm{d}t} = -\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_i}+\frac{1}{\rho}\frac{\partial}{\partial x_j}[\overline{\tau}_{ji}+(-\rho\overline{u'_ju'_i})]

（雷诺平均N-S方程，其中被称为雷诺应力）

且有湍动能：

k=\frac{1}{2}\overline{u'_iu'_i}

4.2.2 K41理论

注入能量后，湍流涡的变化可以描述为：
生成->惯性->耗散
三个相对有区别的过程：
涡的过程
过程中涡的尺度不断变小。且有：

最大涡尺度：（最大涡尺度受边界的限制：，，）——生成阶段
泰勒尺度：——惯性阶段
最小涡尺度：（最小涡尺度下惯性力和粘性力相等：）——耗散阶段

大涡的速度和时间尺度大于小涡：
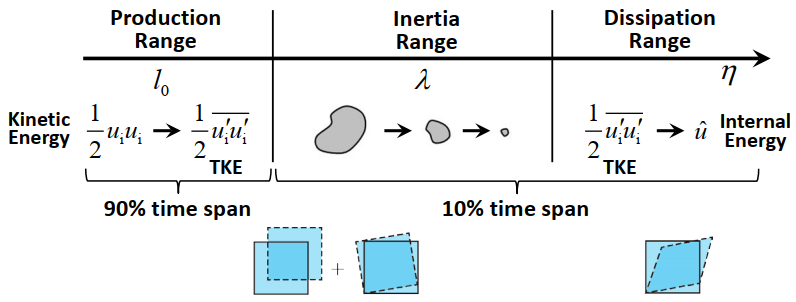
涡的运动变形和时间跨度

在涡的生成耗散的动态平衡中，能量的耗散率等于能量注入率（生成尺度下的大涡能量生成率）。
大涡的能量：
大涡下的时间：
于是得到大涡的能量生产率，也是能量耗散率：

\epsilon=\mathrm{d}k/\mathrm{d}t \sim \frac{u_0^3}{l_0} \tag{4.2.2.1}

对于耗散尺度下的小涡，惯性力和粘性力相近：，得到：

\frac{1}{t_k} \sim \frac{\nu}{\eta^2}

耗散率也可以写作：
于是得：

\epsilon \sim \frac{\nu u_k^2}{\eta^2} \tag{4.2.2.2}

再次利用耗散尺度下惯性力和粘性力相近，雷诺数近似于1：得：

\eta \sim (\frac{\nu^3}{\epsilon})^{1/4} \tag{4.2.2.3}

由和得生成尺度和耗散尺度的比较式：

\frac{l_0}{\eta} \sim (\frac{u_0l_0}{\nu})^{3/4}=Re_L^{3/4} \tag{4.2.2.4}

在惯性过程中，大涡将能量传递给小涡，
用波数代替尺度（）
能量可视为波数和耗散率的函数：
利用量纲分析的大Π定理可以求得：

E \sim k^{-5/3}\epsilon^{2/3}

则有下面的图：
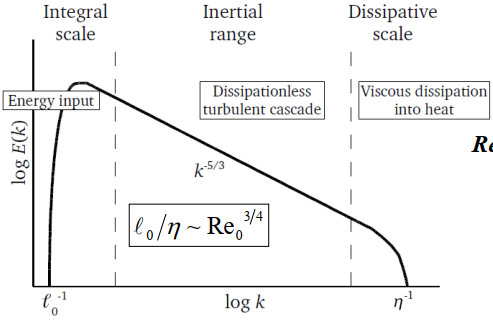
涡的能量变化

偶生牵绊始成涡
代代相传子女多
团团絮絮终成梦
耗尽余力归蹉跎

4.3 湍流边界层

4.3.1 间歇因子

湍流情况下，边界层会有层流、湍流交替出现的现象。按湍流和层流所占时间的比例定义间歇因子：
在壁面出总是湍流，；在足够远的外流区总是层流，。如图所示：
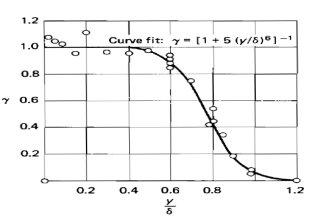
平板湍流边界层间歇因子
对于平板，一般来说：一下一直是湍流（）；以上的一直是层流（）。

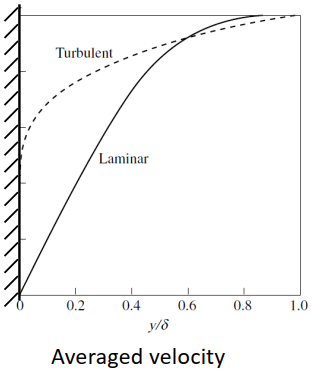
4.3.2 湍流边界层中的速度形

湍流边界层速度形比层流边界层饱满：
湍流、层流边界层平均速度形

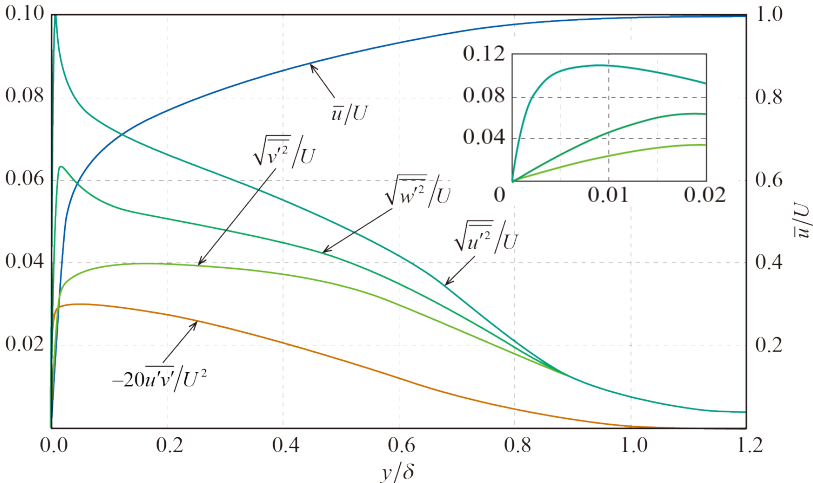
设壁面处的剪切力为。近似于雷诺应力的形式，令。被称为壁面摩阻速度：

u_\tau = \sqrt{\tau_w/\rho}

在此基础上，可以构造出无量纲量：

y^+ = \frac{u_\tau y}{\nu}\\
u^+ = \frac{u}{u_\tau}

（和湍流涡的雷诺数有关联）

用这两个无量纲量表示速度形，并以此来分区：
湍流边界层分层
总的来说可以分为有重叠的内层和外层，
内层又可以分为粘性底层和对数层，粘性底层又可以分为线性底层和过渡区域，
线性底层-过渡层-对数层-剩余外层-主流之间的分隔高度（）分别为：7、50、1000、10000。

其速度分布分别为：
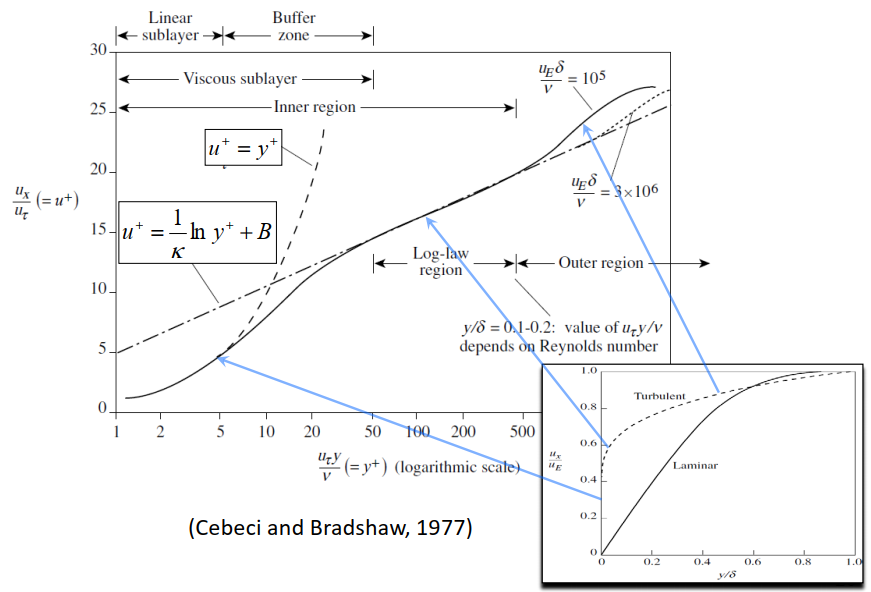
无量纲化湍流边界层速度型
线性底层：
过渡层：光滑过渡上下两层
对数层：
外层：

除此之外，其剪切力分布为：
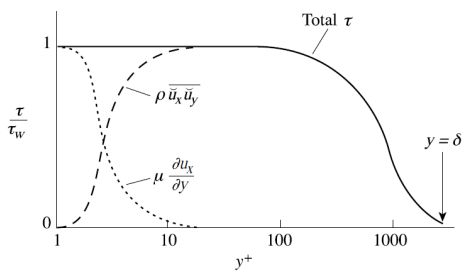
湍流边界层雷诺应力分布
在粘性底层内总剪切力不变，但是雷诺应力所占比例迅速增大，平均流剪切力迅速减少，最后剪切力全部为雷诺应力。从对数层后开始，总剪切力减少最后接近零。

本文章使用limfx的vscode插件快速发布