粘性流体力学期末总结(二)
Chapter 4. Turbulent Flow
4.4 管流
在直管中,管流可以分段:进口段、完全发展段:

开始进入时,存在可被视为无粘的区域(无粘核心)和与壁面接触的边界层,这里叫做进口段。
无粘核心会不断减小,边界层变厚,最后无粘核心消失,管内全部为边界层。进入完全发展段。
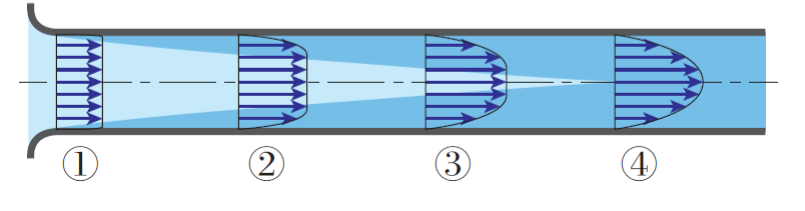
如果是层流,完全发展段则表现为哈根-泊肃叶流动。
在湍流的完全发展段速度形和剪切力分布如图所示:

作业题试解
Assignment 1:
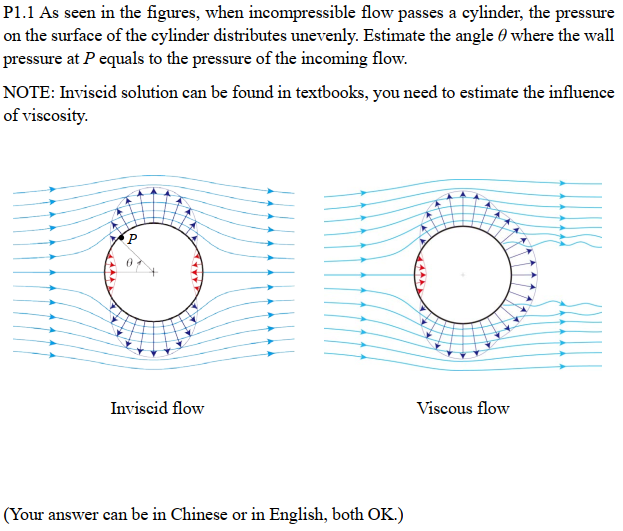
解:
无粘情况下流函数为:
\phi(r,\theta) = -V_\infin(r+\frac{R^2}{r})\cos\theta
其速度为:
\left\{
\begin{aligned}
&V_\theta = \frac{1}{r}\frac{\partial \phi}{\partial \theta}= V_\infin(1+\frac{R^2}{r^2})\sin\theta\\
&V_r = \frac{\partial \phi}{\partial r} = - V_\infin(1-\frac{R^2}{r^2})\cos\theta\\
&V = \sqrt{V_\theta^2+V_r^2} = V_\infin\sqrt{1-\frac{2R^2}{r^2}\cos2\theta+\frac{R^4}{r^4}}
\end{aligned}
\right.
可得在壁面处的速度为,
当时,,则由伯努利原理得:
在有粘情况下,受边界层的排挤,无粘流会往外扩大,此时,要使
V_\infin\sqrt{1-\frac{2R^2}{r^2}\cos2\theta+\frac{R^4}{r^4}}\Bigg|_{r>R} = V_\infin
即:
\cos2\theta = \frac{R^2}{r^2}\Big|_{r>R}
则:
|\theta|>\frac{\pi}{6}
Assignment 2:

P2.1
解:
由高斯定理得:
\iint_{CS} \phi u_i\delta_i \mathrm{d}A = \iiint_{CV} \bigtriangledown_i(\phi u_i) \mathrm{d}B
其中:
\bigtriangledown_i(\phi u_i) = u_i\bigtriangledown_i\phi + \phi\bigtriangledown_iu_i
所以:
\iint_{CS} \phi u_i\delta_i \mathrm{d}A = \iiint_{CV} [u_i\bigtriangledown_i\phi + \phi\bigtriangledown_iu_i] \mathrm{d}B \tag{1}
由于控制体体积不随时间改变,则:
\frac{\mathrm{d}}{\mathrm{d}t}\iint_{CV}\phi\mathrm{d}B = \iiint_{CV}\frac{\partial \phi}{\partial t}\mathrm{d}B \tag{2}
对于拉格朗日法中的,其体积随时间改变:
\begin{aligned}
\frac{\mathrm{d}}{\mathrm{d}t}\iiint_{sys} \phi\mathrm{d}B &= \iiint_{CV}\frac{\mathrm{d}\phi}{\mathrm{d}t}\mathrm{d}B + \iiint_{sys}\phi\frac{\mathrm{d}(\delta B)}{\mathrm{d}t}\\
&= \iiint_{CV}\frac{\mathrm{d}\phi}{\mathrm{d}t}\mathrm{d}B + \iiint_{sys}\phi\frac{\mathrel{d}(\delta B)}{\mathrel{d}t}\frac{1}{\delta B} \delta B\\
&= \iiint_{CV}\frac{\mathrm{d}\phi}{\mathrm{d}t}\mathrm{d}B + \iiint_{sys}\phi\frac{\mathrel{d}(\delta B)}{\mathrel{d}t}\frac{1}{\delta B} \mathrm{d} B
\end{aligned}
由于速度的散度代表体系体积变化率,即:
\bigtriangledown_iu_i = \frac{1}{\delta B}\frac{\mathrm{d}(\delta B)}{\mathrm{d}t}
代入上式得:
\begin{aligned}
\frac{\mathrm{d}}{\mathrm{d}t}\iiint_{sys} \phi\mathrm{d}B &= \iiint_{CV}\frac{\mathrm{d}\phi}{\mathrm{d}t}\mathrm{d}B + \iiint \phi\bigtriangledown_i(u_i) \mathrm{d}B\\
&= \iiint_{CV}[\frac{\mathrm{d}\phi}{\mathrm{d}t}+\phi\bigtriangledown_iu_i]\mathrm{d}B
\end{aligned}
\tag{3}
将代入雷诺运输方程中:
\iiint_{CV}[\frac{\mathrm{d}\phi}{\mathrm{d}t}+\phi\bigtriangledown_iu_i]\mathrm{d}B = \iiint_{CV}[\frac{\partial \phi}{\partial t}+\frac{\mathrm{d}\phi}{\mathrm{d}t}+\phi\bigtriangledown_iu_i]\mathrm{d}B
去掉积分号:
\frac{\mathrm{d}\phi}{\mathrm{d}t} = \frac{\partial \phi}{\partial t} + u_i\bigtriangledown_i\phi
得到物质导数。
P2.2
取流体微团:
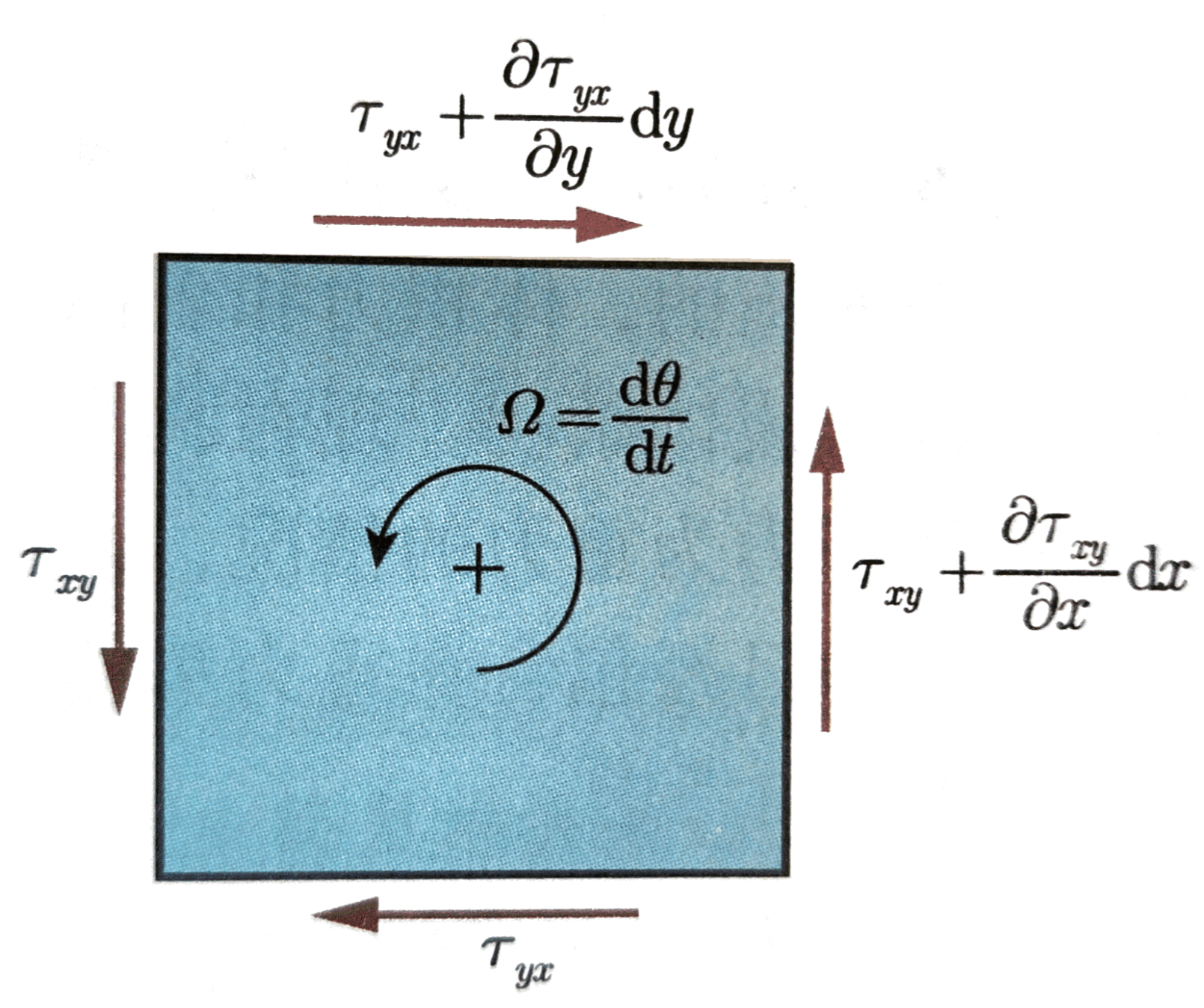
由相对于质心的动量矩方程得:
[(\tau_{xy}+\frac{1}{2}\frac{\partial \tau_{xy}}{\partial x}\mathrm{d}x) - (\tau_{yx}+\frac{1}{2}\frac{\partial \tau_{yx}}{\partial y}\mathrm{d}y)]\mathrm{d}x\mathrm{d}y\mathrm{d}z = \frac{1}{12}\rho\mathrm{d}x\mathrm{d}y\mathrm{d}z[(\mathrm{d}x)^2+(\mathrm{d}x)^2]\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}
忽略高阶小量得:
\tau_{xy}=\tau_{yx}
同理可以求出其余两个方向的角动量方程,于是得:
\tau_{ij}=\tau_{ji}
Assignment 3:
P2.3 An infinitesimal volume of gas passes a turbojet engine from inlet to exhaust nozzle. Try to describe its energy change in detail step by step along the path.
(You need to describe the change of total energy, kinetic energy and internal energy, and how it happens.)
NOTE: Assuming this gas particle does not take part in chemical reaction.
解:
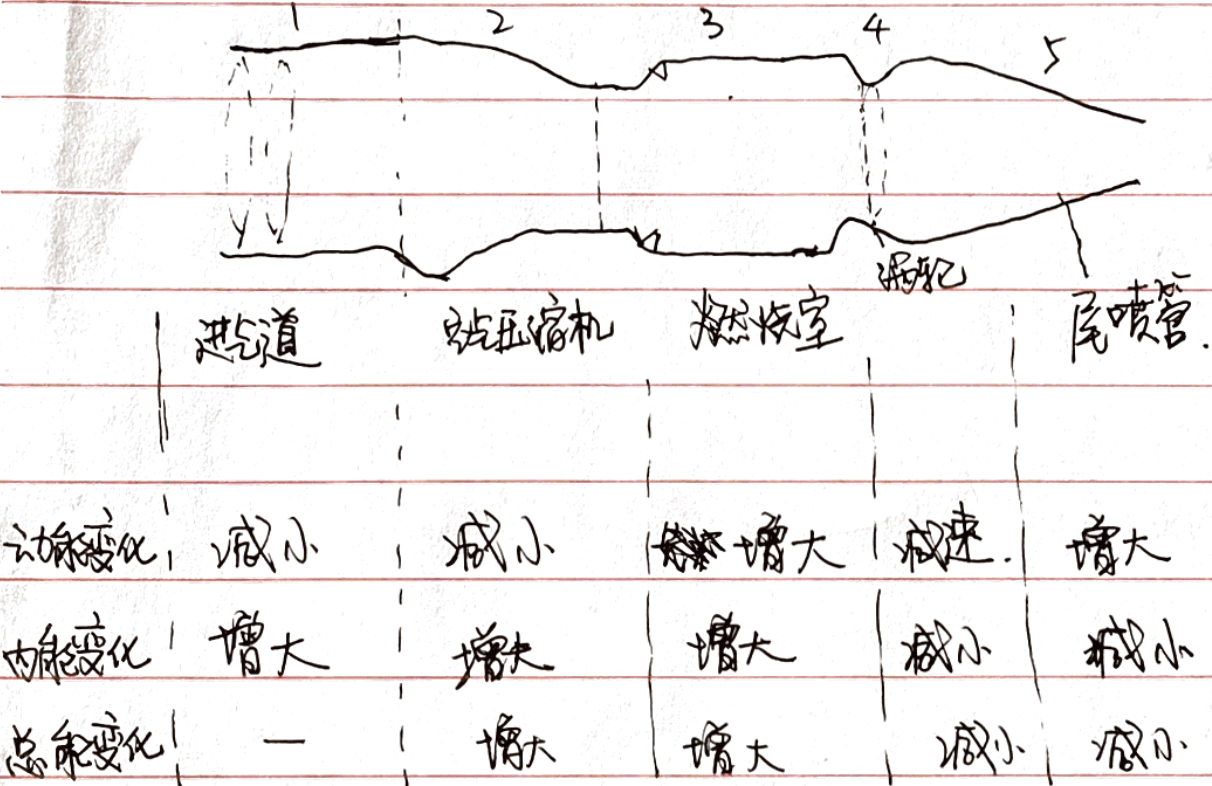
Assignment 4:

P3.1
解:
设题设中的变量满足方程:
F(v,D,c,\rho,\mu,\tau) = 0
他们的量纲分别为:
\left\{
\begin{aligned}
&[v]=LT^{-1}\\
&[D]=L\\
&[c]=LT^{-1}\\
&[\rho]=ML^{-3}\\
&[\mu]=ML^{-1}T^{-1}\\
&[\tau]=ML^{-1}T^{-2}
\end{aligned}
\right.
设在量纲分析体系下它们满足:
[v^{x_1}D^{x_2}c^{x_3}\rho^{x_4}\mu^{x_5}\tau^{x_6}] = \Pi
于是可建立线性方程组:
\begin{bmatrix}
0&0&0&1&1&-1\\
1&1&1&-3&-1&1\\
-1&0&-1&0&-1&2
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3\\
x_4\\
x_5\\
x_6\\
\end{bmatrix}
=0
可解得解向量:
\begin{bmatrix}
1\\
0\\
-1\\
0\\
0\\
0
\end{bmatrix}
\,\,\,\,
\begin{bmatrix}
1\\
1\\
0\\
1\\
-1\\
0
\end{bmatrix}
\,\,\,\,
\begin{bmatrix}
2\\
0\\
0\\
-1\\
0\\
1
\end{bmatrix}
这三个向量对应三个无量纲数:
Ma = \frac{v}{c}\,\,\,Re=\frac{\rho vD}{\mu}\,\,\,\Pi_3=\frac{v\tau}{\rho}
所以有:
G(Ma,Re,\frac{v\tau}{\rho}) = 0
即:
\tau = \frac{\rho}{v}f(Ma,Re)
P3.2
解:
去如图所示微团:

定常流情况下,微团处于力平衡状态:
p \cdot \pi r^2 - (p+\frac{\partial p}{\partial x}\mathrm{d}x)\pi r^2 = \tau\cdot 2\pi r\mathrm{d}x\\
\Rightarrow -\frac{\partial p}{\partial x} = \frac{2\tau}{r}
代入牛顿内摩擦定律得:
\frac{\partial u}{\partial r}=\frac{\partial p}{\partial x}\frac{r}{2\mu}
管流相对于管轴线中心对称,则只是的函数:
\frac{\mathrm{d} u}{\mathrm{d} r}=\frac{\partial p}{\partial x}\frac{r}{2\mu}
由于微团在方向没有运动,则沿着方向压强不变,所以,又只是的函数,于是,所以:
\frac{\mathrm{d} u}{\mathrm{d} r}=\frac{\mathrm{d} p}{\mathrm{d} x}\frac{r}{2\mu}
代入壁面不滑移条件:
u=0\,\,\,(r=R)
积分得:
u=-\frac{1}{4\mu}\frac{\mathrm{d}p}{\mathrm{d}x}(R^2-r^2)
Assignment 5:
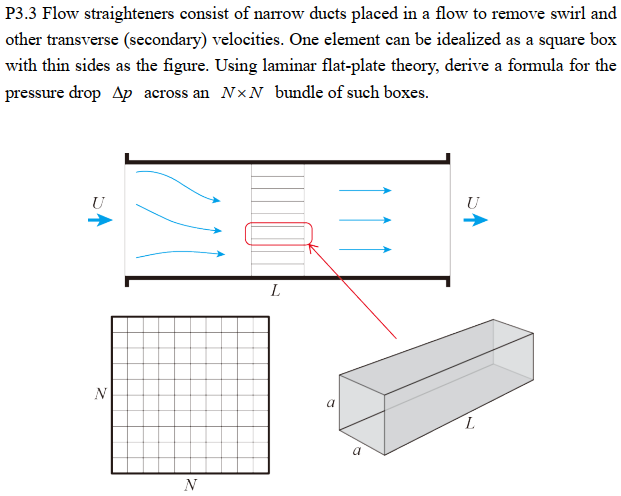
解:
如图所示为其中一个栅格的边界层示意图:

边界层较薄,边界层外视为无粘,故可以采用伯努利方程,压降为:
\Delta p = \frac{1}{2}\rho u_2^2 - \frac{1}{2}\rho u_1^2
\tag{1}
利用平板边界层的布拉修斯解:
\delta^*=\frac{1.72}{\sqrt{Re_x}}x
其中:
Re_x = \frac{\rho UL}{\mu}\\
x=L
所以截面2处的位移厚度为:
\delta^* = 1.72\sqrt{\frac{\mu L}{\rho U}}
\tag{2}
略去边界层,截面2处的流量为:
m_2=u_2(a-2\delta^*)^2
截面1处的流量为:
m_1=u_1a^2
由连续性条件得,则:
u_2(a-2\delta^*)^2 = u_1a^2
\tag{3}
联立,其中,得:
\Delta p = \frac{1}{2}\rho U^2[(\frac{a}{a-2\delta^*})^4-1]\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(\delta^* = 1.72\sqrt{\frac{\mu L}{\rho U}})
Assignment 6:
P4.1 Write a short essay to discuss the relationship among Reynolds number, separation, and transition. At least one flow example is required to be included.
答:

Assignment 7:
P4.2 To estimate surface friction of turbulent boundary layer, Many engineers are willing to use an empirical formula proposed by Schoenherr in 1932:
\frac{1}{\sqrt{C_f}} = 4.15\log_{10}({\rm Re}_xC_f)+1.7
Assume standard temperature and pressure air flowing over a flat-plate for .
- Estimate the shear stress at ;
- Find the thickness of viscous sublayer in mm.
解:
由和得:
{\rm Re}_xC_f=\tau\frac{U\mu}{2L}\\
C_f=\tau_f/p
带入经验公式得:
{\rm e}^{-\frac{1}{2}\lg\tau_f}\sqrt{p}=4.15\lg\tau_f+4.15\lg\frac{U\mu}{2L}+1.7
可写作:
x=a{\rm e}^{-\frac{1}{2}x}+b
其中:
\begin{aligned}
x&=\lg \tau_f\\
a&=\frac{\sqrt{p}}{4.15}\\
b&=-(\lg\frac{U\mu}{2L}+\frac{1.7}{4.15})
\end{aligned}
经过迭代得(牛顿迭代法):
\tau_f=14244.86\,{\rm Pa}
在湍流边界层中,粘性底层的无量纲厚度为50,即:
y^+ = \frac{u_\tau y}{\nu} = 50
其中:
u_\tau = \sqrt{\frac{\tau_f}{\rho}}
代入即可求得:
综上:
\tau_f=14244.86\,{\rm Pa}\,\,\,\,\delta_0=0.00705\,{\rm mm}
Newton迭代法代码:
#include<stdio.h>
#include<math.h>
#include<string.h>
#define RHO (1.293) // 标准大气密度
#define MU (17.9e-6) // 动力粘度
#define U (50.0) // 主流速度
#define L (1.0) // x方向位置
#define MAXSTEPS (100) // 最大迭代次数
#define EPSILON (1e-4) // 计算精度
double phi(double x,double a,double b);
int main()
{
double eps=1e100;
int ifGetAnswer=1;
int steps=0;
double p = 0.5*RHO*U*U;
double a = sqrt(p)/4.15;
double b = -(log10((U*MU)/(2*L))+1.7/4.15);
double x = 1.0;
double tau = 0.0;
while (eps>EPSILON)
{
double x_temp = phi(x,a,b);
steps++;
if (steps==MAXSTEPS)
{
ifGetAnswer = 0;
break;
}
eps = fabs(x_temp-x);
x=x_temp;
}
if (ifGetAnswer)
{
tau = pow(10.0,x);
printf("τ=%0.3lf\n",tau);
FILE *fp=fopen("Answer.txt","w");
if (fp!=EOF)
{
if (fprintf(fp,"τ=%0.3lf",tau))
{
printf("结果已写入文件Answer.txt\n");
}
else
{
printf("结果无法写入文件!\n");
}
fclose(fp);
}
else
{
printf("结果无法写入文件!\n");
}
}
else
{
printf("超过最大迭代次数,求解失败!\n");
}
printf("按回车以继续。");
getchar();
return 0;
}
double phi(double x,double a,double b)
{
double fx=a*exp(-0.5*x)+b-x;
double deri=a*(-0.5)*exp(-0.5*x)-1;
return x-fx/deri;
}
Assignment 8:
P4.3 A cup of water weighted 1 kg is stirred by an electronic blender of 10 Watt. Try to estimate the size of the smallest eddies.
P4.4 Estimate the size of dissipation eddies for a turbulent boundary layer with mainstream speed of 50 m/s and nominal thickness of 10 mm.
P4.3
解:
耗散率和输入功率相等:
由K41理论得:
\eta \sim (\frac{\nu^3}{\epsilon})^\frac{1}{4}
代入水的运动粘度和耗散率得涡的最小尺度:
\eta = 17.87 \mathrm{\mu m}
P4.4
解:
在湍流边界层中,稳定湍流区在对数层里:
外层无量纲高度(约为10000)对应边界层厚度:
其中:
综上得:
即最大涡尺度
最大涡雷诺数
由K41理论得,耗散尺度为:
\eta = l_0/Re_L = 0.001\,\mathrm{mm}
Assignment 9:
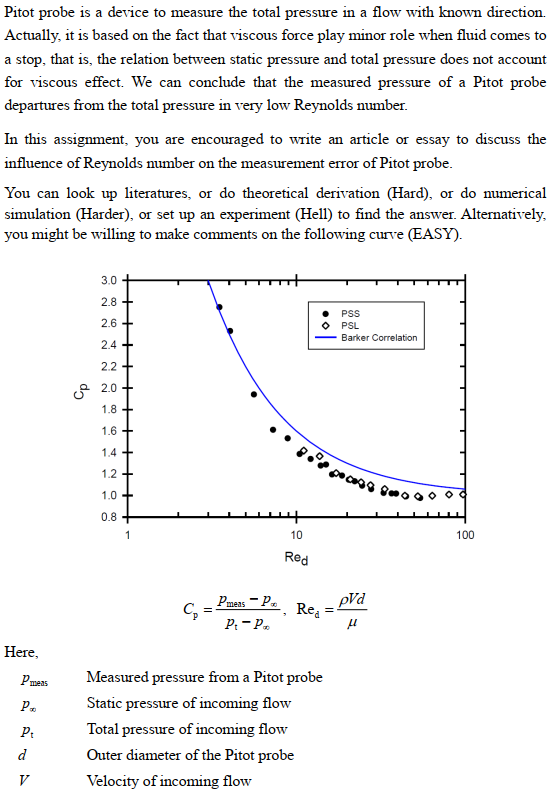

Assignment 10:
-
One of the most important aspects is that the stochastic/random nature of turbulent flows is its intrinsic property. Navier–Stokes equations are deterministic. Is it the correct formulation of turbulent flow? How can a deterministic equation exhibit a random solution?
-
What is "closure problem" in turbulent flow?
本文章使用limfx的vscode插件快速发布