模拟退火算法——SimulatedAnnealing
类介绍
本类是退火算法类,用退火算法解决优化问题。与 MATLAB 自带退火算法不同点是:MATLAB 自带退 火算法是寻找某函数最优解,即目标函数必须写成显函数的形式,而在很多实际问题中,目标函数很难 用函数表示,需要自己写出一个 m 文件计算目标函数,本类致力于解决此类问题。
使用本类,您至少需要编写 3 个函数,分别是产生一组初始方案,对该方案进行扰动,计算目标函数, 根据需要您可以选择性编写计算辅助值的函数。编写规则参考类属性的函数句柄参数。
使用本类至少具有以下优点:
只需要编写根据具体问题抽象出来的逻辑文件,不需要自己编写固定的退火算法框架。 类中有特定的属性存储求解过程中的数据,不需要自己编写繁琐的代码存储数据,需要什么数据即 可以从类属性中获取。
类中具有特定的作图函数,可以非常方便做出指定数据随降温度数和降温次数的变化图,用于分析 模型的性能。
运用本类时,目标函数取最小值,如果想要取最大值,求其相反数即可。
类属性
算法参数
属性名称 | 属性说明 | 默认值 |
|---|---|---|
alpha | 温度衰减系数 | 0.9 |
T_begin | 退火开始温度 | 97 |
T_end | 退火终止温度 | 3 |
markovLength | markov链长度 | 1000 |
beta | 概率函数系数 | 1 |
beta 说明
退火算法中,当目标函数大于当前接受最优解时,有一定概率接受,接受概率函数为:
\[ f=exp(\frac{E_{current}-E_{new}}{\beta T_{now}}) \]
其中 \(E_{current}\) 为当前接受最优解,\(E_{new}\) 为当前目标函数值,\(T_{now}\) 为当前温度。
概率函数应当在温度很高时比较大,而在温度很低时概率几乎为0。由于不同情况 \(E\) 大小有很大区别, 所以需要选择合适的 \(\beta\) 值。
函数句柄参数
firstFunctionHandle
产生第一组解的函数句柄。
此函数不能有输入参数,有且只有一个输出参数 plan。plan 必须是一个元胞数组(1×n),存储了新生成方案的数据。
changePlanFunctionHandle
扰动函数句柄。
输入必须是 firstPlanFunctionHandle 函数输出的元胞数组 plan,输出一个更改了数据的元胞数组,即进行退火算法中的 “扰动”。
dependentDataFunctionHandle
计算辅助值函数句柄。
输入必须是 firstPlanFunctionHandle 函数输出的元胞数组 plan,输出一个另外的元胞数组dependentData (1×n),里面包含了任意的数据。此函数可以省略。此函数的目的是通过 plan 计算 一些辅助数据,方便目标函数计算和之后的分析。
goalFunctionHandle
计算目标函数函数句柄。
此类中 dependentDataFunctionHandle 不为空,则其输入必须是(plan,dependentData),如果为 空,说明没有要计算的辅助值,输入必须是 (plan)。
输出必须是一个实数,即计算的目标函数。目标函数必须是求最小值,如果是求最大值要取相反数。
coolingTimes(非独立属性)
根据已有参数,计算得到的降温次数。
计算结果属性(只读)
planBest
最佳方案元胞数组
dependentDataBest
最佳方案非独立属性的元胞数组
goalBest
最佳方案的目标函数值
temperatureHistory
退火过程中降温度数的记录(跟 T_begin 相比降低的度数)
posibilityHistory
记录每个温度下接收概率的数据,m × 4 矩阵。每一行是一个温度,第 1 列是此温度下出现的最低概率,第 3 列是出现过的最小概率,第 2 列是概率平均值,第 4 列是概率出现的次数(即当前解不如接受 解出现次数)
planHistory_best
历史最优方案的历史记录,元胞数组,根据函数 firstPlanFunctionHandle 产生的 plan 数组,将 1 × n扩展到 m × n,每一行是一个温度下的数据,m 即为降温次数。
dependentDataHistory_best
历史最优非独立数据的历史记录,元胞数组,整合了每个温度下函数 dependentDataFunctionHandle 产生的 dependentData 数组。
goalHistory_best
历史最优目标函数的历史记录。由于目标函数只能是一个实数,所以此属性是 m × 1 的矩阵。
planHistory_current
当前接受最优方案的历史记录,结构同 planHistory_best
dependentDataHistory_current
当前接受最优非独立数据历史记录,结构同 dependentDataHistory_best
goalHistory_current
当前接受最优目标函数历史记录,结构同 goalHistory_best
dependentDataNumber
非独立数据元胞数组的长度
planNumber
方案元胞数组的长度
ifHaveDependentData
逻辑值,是否有非独立数据。
类方法
构造函数
obj = SimulatedAnnealing(firstPlan,changePlan,getGoal, getDependentData)
输入参数为对应函数句柄,均可省略。
功能函数
judge(obj)
对当前类函数句柄进行简单的判断。可以判断函数内部是否有语法错误,输入输出是否按照要求。
solve(obj)
求解模型,在命令行会有进度提醒,方便安排时间。训练完成后可以在类属性中查看训练情况
作图函数
以下函数,h 为输出的图像句柄,包含了图中所有元素的句柄,可省略。ax 为坐标区句柄,可省略。
h = plotGoal(obj,ax)
作目标函数随退火温度和退火次数变化图。
如果省略 ax,会在同一 figure 下作目标函数随降温次数和降温度数两幅图。如果指定 ax,只作随降温
次数变化图。
h = plotPosibility(obj,ax)
作接受概率平均值随退火温度和退火次数变化图。
如果省略 ax,会在同一 figure 下作平均概率随降温次数和降温度数两幅图。如果指定 ax,只作随降温 次数变化图。
h = plotPlan(obj,index,name)
作方案元胞数组中某变量随退火温度和退火次数变化图。
index 为此变量在 plan 数组中的序号,此变量必须是一个实数。 name 是此变量的名称,可省略。
h = plotDependentData(obj,index,name)
作非独立元胞数组中某变量随退火温度和退火次数变化图。
index 为此变量在 dependentData 数组中的序号,此变量必须是一个实数。 name 是此变量的名称, 可省略。
h = plotFigure(obj)
作目标函数、平均接受概率随退火温度和退火次数变化图,即调用 plotGoal 和 plotPosibility ,用于分析模型性能。
MATLAB 自带函数 evalin
v = evalin('base', 'var')
模型有时候可能会需要一些常量,比如旅行商问题的距离矩阵。介绍 evalin 函数最简单的用法,解决此 问题。
参数中‘base’表示主工作区,即没有调用函数时的工作区,不能更改。‘var’ 是主工作区变量名称,必须带 ‘’。v = evalin('base', 'var') 即将主工作区变量 var 赋值给函数工作区变量 v。
解决上述问题方法即将常量存储在主工作区,在函数内部用 evalin 函数将常量传入即可。
实例一:TSP旅行商问题
经典的问题不再赘述,我们先处理数据得到 52 个城市之间的距离矩阵:
% SA1_prepare
clear
coordinates_x = [565 25 345 945 845 880 25 525 580 650 1605 1220 1465 ...
1530 845 725 145 415 510 560 300 520 480 835 975 1215 1320 1250 660 ...
410 420 575 1150 700 685 685 770 795 720 760 475 95 875 700 555 830 ...
1170 830 605 595 1340 1740];
coordinates_y = [575 185 750 685 655 660 230 1000 1175 1130 620 580 200 5 ...
680 370 665 635 875 365 465 585 415 625 580 245 315 400 180 250 555 ...
665 1160 580 595 610 610 645 635 650 960 260 920 500 815 485 65 610 ...
625 360 725 245];
amount = size(coordinates_x,2);
dist_matrix = zeros(amount);
for i = 1:amount
for j = 1:amount
dist_matrix(i,j) = sqrt((coordinates_x(i)-coordinates_x(j)).^2 +...
(coordinates_y(i)-coordinates_y(j)).^2);
end
end
我们先编写初始方案的函数,用一个 1 × 52 的数组即可存储,分别表示先后到达目的地的序号。
function planCell = SA1_firstPlan()
plan = randperm(52);
% 将结果以元胞数组形式保存
planCell = {plan};
end
再编写扰动的方案,此问题很简单,随机改变两个位置或三个位置即可。
function newPlanCell = SA1_changePlan(plan)
% 参数名称不一定要和 firstPlan 输出一样,但是必须正确从中取值
% 输入是元胞数组,首先取值
plan = plan{1};
randData = rand();
% 60% 概率交换两地顺序 40% 交换三地顺序
indexOne = randi(52);
indexTwo = randi(52);
if randData < 0.6
while indexOne == indexTwo
indexOne = randi(52);
end
temp = plan(indexOne);
plan(indexOne) = plan(indexTwo);
plan(indexTwo) = temp;
else
indexThree = randi(52);
while indexOne == indexTwo || indexOne == indexThree || ...
indexTwo == indexThree
indexOne = randi(52);
indexTwo = randi(52);
end
temp = plan(indexOne);
plan(indexOne) = plan(indexTwo);
plan(indexTwo) = plan(indexThree);
plan(indexThree) = temp;
end
% 返回结果
newPlanCell = {plan};
end
本问题不需要计算辅助参数,直接编写计算目标函数的文件
function goal = SA1_goal(plan)
% 从元胞数组中获取信息
plan = plan{1};
% 读取主工作区常量
distance = evalin('base','dist_matrix');
goal = 0;
for i = 1:51
goal = goal + distance(plan(i),plan(i+1));
end
goal = goal + distance(plan(1),plan(end));
end
用类进行求解:
SA1 = SimulatedAnnealing(@SA1_firstPlan, @SA1_changePlan, @SA1_goal);
SA1.solve();
SA1.plotFigure();
命令行输出:

作图如下:

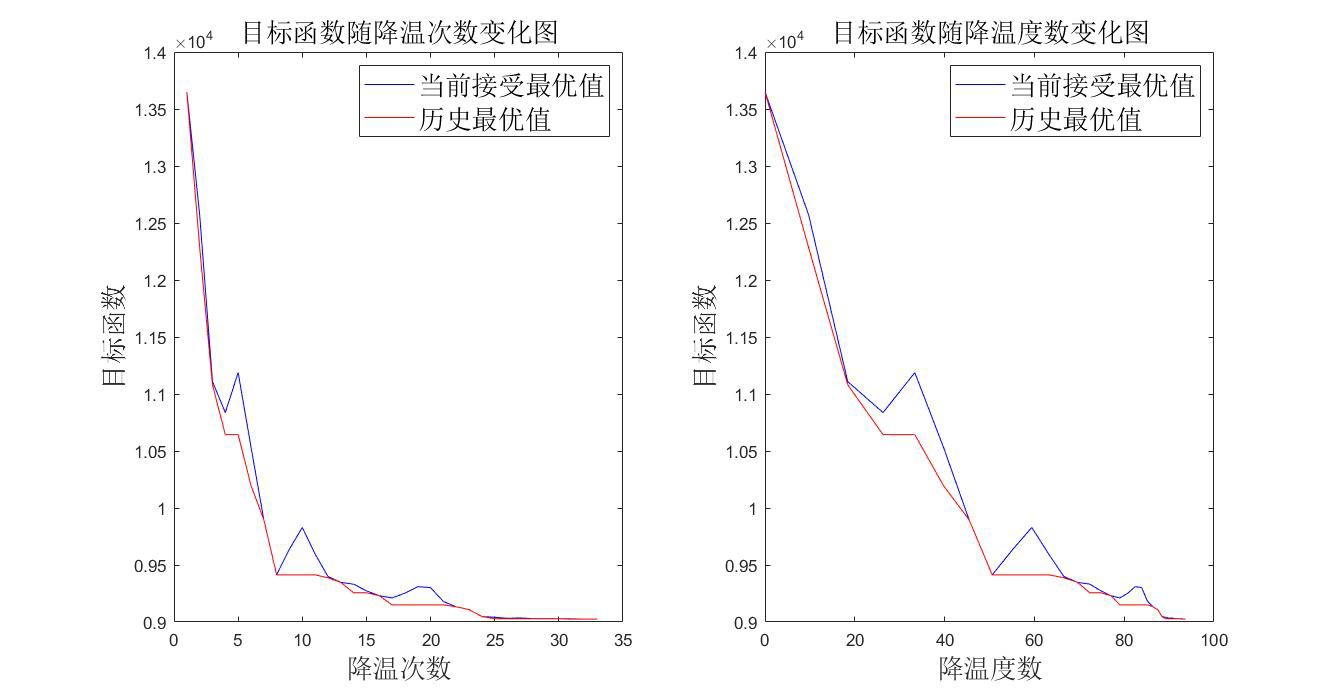
计算过程中,我们发现计算很快,可以增加降温次数。由于开始时平均接受概率比较低,我们增大初始 温度,增大衰减系数,重新求解,代码如下:
SA1 = SimulatedAnnealing(@SA1_firstPlan,@SA1_changePlan,@SA1_goal);
SA1.T_begin = 300;
SA1.alpha = 0.98;
SA1.markovLength = 10000;
SA1.solve();
SA1.plotFigure();
效果图如下,明显性能变好。
想要画出路线图,从 SA1 中取出属性 planBest 即可:
plan = SA1.planBest{1};
xData = zeros(1,52);
yData = zeros(1,52);
for i = 1:52
xData(1,i) = coordinates_x(plan(i));
yData(1,i) = coordinates_y(plan(i));
end
xData(1,53) = xData(1,1); 9 yData(1,53) = yData(1,1);
plot(xData,yData,'b*-');
fh = FigureHandle2D(gca);
fh.plotDecoration('横坐标定位','纵坐标定位','旅游路线图');
fh.setFontSize(16);
(FigureHandle2D 为自定义类)
实例二:排班问题
问题描述
某公司需要6名员工(A-F)值50天的班。每天安排2人值班。
若A不能和C或E排在一起, B不能和F排在一起,A和D排在一起不能超过3天,C只愿意和F排在一起。 AB值班后必排DF值班。请给出一个尽可能公平、合理、劳逸结合的值班次序。( 劳逸结合指尽量避免 连续值班的情况)
问题求解
解决问题的关键在于如何对方案进行扰动。本题中,假设给出了一组初始方案,我们进行扰动的方法是 任意更改几个位置的人员安排,那么还需要满足题目所给的条件。所以我们需要编写一个额外的辅助函 数,帮助我们把方案修改为满足题目条件的方案。代码如下:
function newPlan = SA2_alterPlan(plan)
% 修改重复
for i = 1:50
while plan(1,i) == plan(2,i)
plan(1,i) = randi(6);
end
end
plan = sort(plan);
% 保证 AD 值班天数为不大于 3
specialDay = 0;
for i = 1:50
if plan(1,i) == 1 && plan(2,i) == 4
if specialDay < 3
specialDay = specialDay + 1;
else
if rand() > 0.5
plan(2,i) = 2;
else
plan(2,i) = 6;
end
end
end
end
% 保证 A 不和 C、E 值班
for i = 1:50
if plan(1,i) == 1 && (plan(2,i) == 3 || plan(2,i) == 5)
if rand() > 0.5
plan(2,i) = 2;
else
plan(2,i) = 6;
end
end
end
% AB 后必定 DF
for i = 1:50
if plan(1,i) == 1 && plan(2,i) == 2 && i ~= 50
plan(1,i+1) = 4;
plan(2,i+1) = 6;
end
end
% B 不和 F
for i = 1:50
if plan(1,i) == 2 && plan(2,i) == 6
plan(2,i) = randi([4,5]);
end
end
% C 只和 F
for i = 1:50
if plan(1,i) == 3 || plan(2,i) == 3
plan(1,i) = 3;
plan(2,i) = 6;
end
end
newPlan = plan;
end
此函数不用传入类中,只需要在产生初始方案函数、扰动函数中调用即可。接下来编写初始方案函数和 扰动函数就很简单了:
function planCell = SA1_firstPlan()
plan = randperm(52);
% 将结果以元胞数组形式保存
planCell = {plan};
end
function newPlan = SA2_changePlan(plan)
randData = rand();
% 取出数据
plan = plan{1};
% 40%概率更改一处
if randData < 0.4
plan(randi(2),randi(50)) = randi(6);
% 40%概率更改两处
elseif randData < 0.8
plan(randi(2),randi(50)) = randi(6);
plan(randi(2),randi(50)) = randi(6);
% 20%概率更改三处
else
plan(randi(2),randi(50)) = randi(6);
plan(randi(2),randi(50)) = randi(6);
plan(randi(2),randi(50)) = randi(6);
end
% 使满足方案,并存入数组
newPlan = {SA2_alterPlan(plan)};
end
目标函数是衡量公平性和劳逸结合性的指标。公平性可以用每个人值班天数的方差衡量,越低越好。劳 逸结合性用每个人两次值班间隔天数衡量,假设一次连续值班目标函数加 3 ,只休息一天值班目标函数加 1。原则上这两个指标按一定比例相加得到目标函数,为方便起见,这里不研究比例系数的影响,假设比例系数取1。
想要得到目标函数,就需要根据排班方案得到每个人排班天数和相邻两次间隔天数。这就是 dependentData。如果想要在模型求解后得到标准差的变化情况,只需要在 dependentData 中加上一 个标准差变量即可。
function data = SA2_dependentData(plan)
plan = plan{1};
dayNumber = zeros(1,6);
for i = 1:6
temp = reshape(plan,1,100);
dayNumber(1,i) = length(temp(temp == i));
end
interval = -1 * ones(6,max(dayNumber)-1);
for i = 1:6
index1 = find(plan(1,:) == i);
index2 = find(plan(2,:) == i);
index = sort([index1,index2]);
restDay = diff(index);
for j = 1:length(restDay)
interval(i,j) = restDay(j);
end
end
% 记录标准差,模型求解后可以得到标准差的分析图
data = {dayNumber,interval,std(dayNumber)};
end
function goal = SA2_goal(~,dependentData)
% ~ 代表方案 plan 元胞数组,计算目标函数不需要用到
% 但是必须用 ~ 占位
interval = dependentData{2};
dayNumber = dependentData{1};
goal = 3 * length(find(interval == 1)) + length(find(interval == 2));
goal = goal + std(dayNumber) * std(dayNumber);
end
用默认值求解:
SA2 = SimulatedAnnealing(); 2 % 先不输入参数
SA2.firstPlanFunctionHandle = @SA2_firstPlan;
SA2.changePlanFunctionHandle = @SA2_changePlan;
SA2.dependentDataFunctionHandle = @SA2_dependentData;
SA2.goalFunctionHandle = @SA2_goal;
SA2.solve();
SA2.plotFigure();

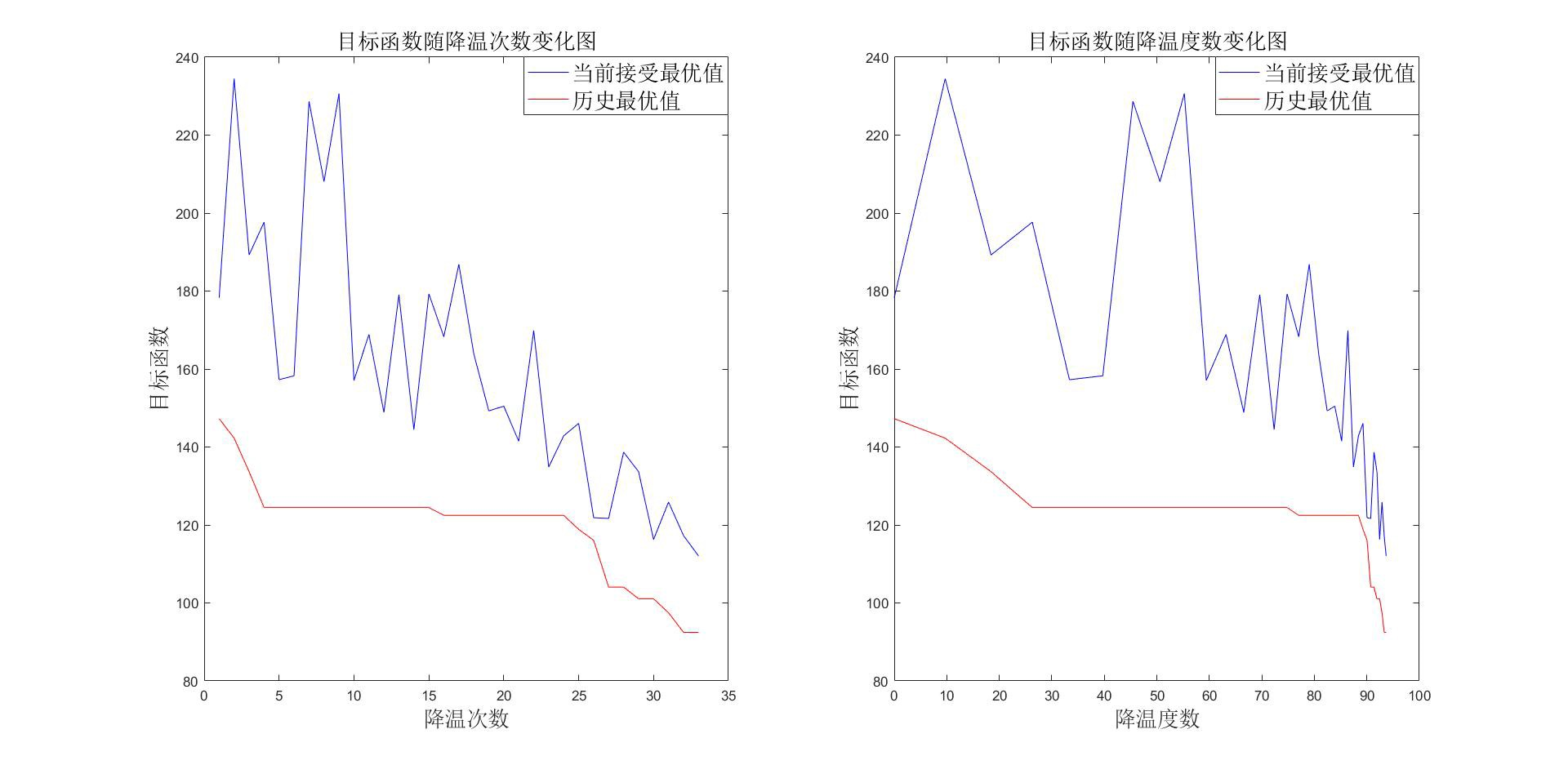
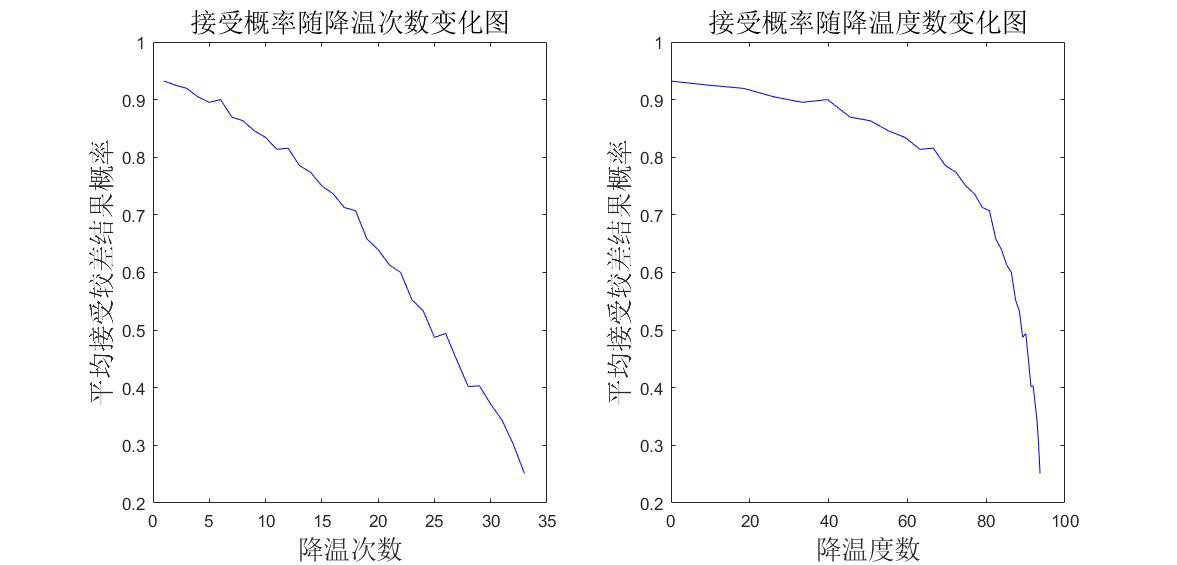
由图,发现接受概率一直很高,说明需要将 beta 参数调小,运行很快,我们可以增大循环次数,调整 参数重新求解:
SA2 = SimulatedAnnealing(); 2 % 先不输入参数
SA2.firstPlanFunctionHandle = @SA2_firstPlan;
SA2.changePlanFunctionHandle = @SA2_changePlan;
SA2.dependentDataFunctionHandle = @SA2_dependentData;
SA2.goalFunctionHandle = @SA2_goal;
SA2.alpha = 0.98;
SA2.beta = 0.008;
SA2.solve();
SA2.plotFigure();
现在想要得到标准差变化,只需要调用 plotDependentData 函数即可
% 数据在第 3 列,名称是 '值班天数标准差'
SA2.plotDependentData(3,'值班天数标准差');
下面可以根据实际情况对方案进行分析,比如作出值班天数的比例图、间隔天数的比例图。
dayNumber = SA2.dependentDataBest{1};
interval = SA2.dependentDataBest{2};
subplot(1,2,1);
pie(dayNumber);
legend('A','B','C','D','E','F');
title('值班天数比例','FontSize',16);
% 观察 interval ,范围是 1~7,说明间隔天数是 0~6
intervalDay = zeros(1,7);
for i = 1:7
intervalDay(1,i) = length(find(interval == i));
end
subplot(1,2,2);
pie(intervalDay);
legend('休息0天','休息1天','休息2天','休息3天','休息4天','休息5天', ...
'休息6天');
title('休息天数分布','FontSize',16);
本文章使用limfx的vsocde插件快速发布







