神经网络简介

数学知识补充：

协方差矩阵向量的协方差矩阵为：

Cov(X)=
\begin{bmatrix}
Var(X_1) & Cov(X_1,X_2) & Cov(X_1,X_3) & \dots & Cov(X_1,X_N)\\
Cov(X_2,X_1) & Var(X_2) & Cov(X_2,X_3) & \dots & Cov(X_2,X_N) \\
Cov(X_2,X_1) & Cov(X_2,X_3) & Var(X_3) & \dots & Cov(X_2,X_N) \\
\vdots & \vdots& \vdots& \ddots&\vdots\\
Cov(X_N,X_1) &Cov(X_N,X_2)&Cov(X_N,X_3)&\dots & Var(X_N)
\end{bmatrix}

：函数取最大最小时参数的取值。
e.g.

x = \argmin_x f(x;\Theta)

表示含参变量的函数在（S为定义域）取最小值时自变量的取值

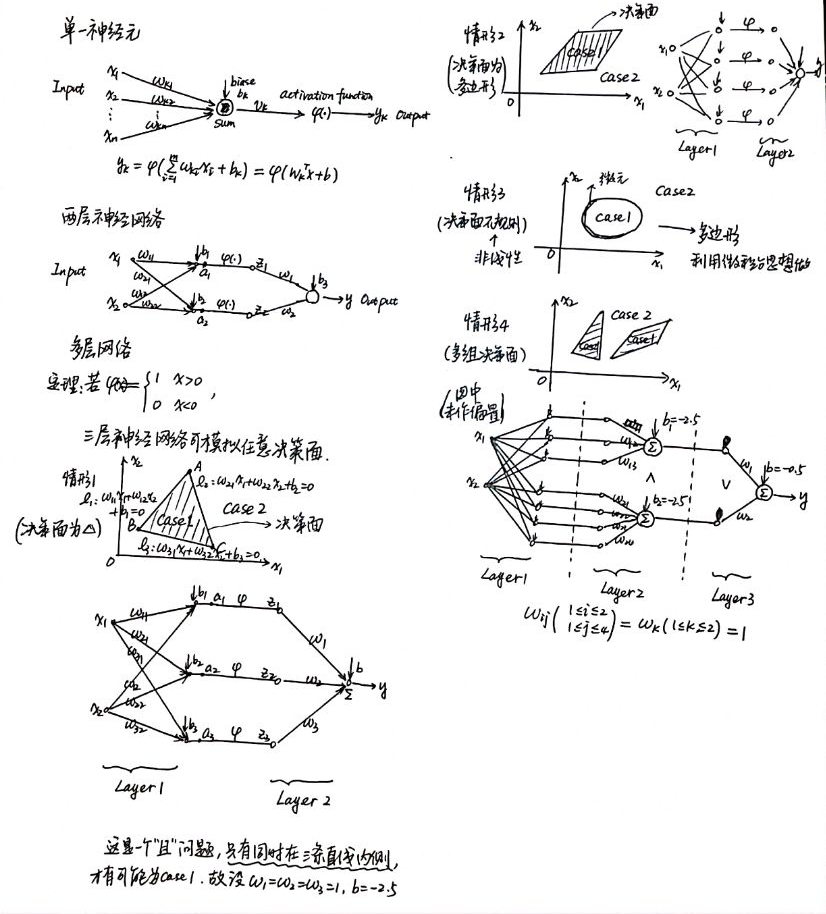
神经元与单层神经网络

人工神经网络是用于模拟人的神经网络。

感知机/单层神经网络

感知器算法

感知器算法（Perceptron Algorithm）:
1. 随机选择和；
2. 取一个训练样本
  - 情形a 若且，则：
  - 情形b 若且，则：
3. 再取另一个，回到步骤2
4. 终止条件：直到所有输入输出对都不满足步骤2中a和b之一，退出循环。
历史意义： 1956年，Frank Rosenblatt成功证明了这个算法。该算法的成功证明，使得这种算法被认为机器学习的最原始算法
结论： 经过以上有限步操作，最终一定能找到一个超平面，使得该平面能够成功将两类分开。

对于输入维向量，定义以下维向量

\vec{x_i}=\begin{bmatrix}
x_i \\
1
\end{bmatrix},\quad 情形a

\vec{x_i}=\begin{bmatrix}
-x_i \\
-1
\end{bmatrix}, \quad 情形b

w=\begin{bmatrix}
w \\ b
\end{bmatrix}

原始问题转化为，经过有限步操作后，一定存在一个超平面：

w^T\vec{x_i}+b>0

定理： 如果存在一个向量，使得，都有，则对感知器算法，经过有限步后，一定存在一个，对，都有

证：不失一般性，设。如果对，都有，那么定理一定成立。否则，假设，使得，则根据感知器算法，，等价于两边取模平方，有：

||w(k+1)-aw_{opt}||^2=||w(k)-aw_{opt}||^2+||\vec{x_i}||^2+2(w(k)-aw_{opt})^T\vec{x_i}

故有：

||w(k+1)-aw_{opt}||^2\leq||w(k)-aw_{opt}||^2+||\vec{x_i}||^2-2aw_{opt}^T\vec{x_i}

定义

\beta=\max_{i=1}^N||\vec{x_i}||,\gamma=\min_{i=1}^N(w_{opt}^Tx_i)(\beta>0,\gamma>0)

若，则有：

||w(k+1)-aw_{opt}||^2\leq||w(k)-aw_{opt}||^2-1 \tag{1}

由假设，易知

||aw_{opt}||=\frac{\beta^2+1}{2\gamma}

再定义

D=||w(0)-aw_{opt}||

至多经过次对式的迭代，有最终收敛于（也就是说，最多次后一定能找到一个，使得原定理成立）

多层神经网络

多层感知机构成的神经网络优缺点

优势：
- 基本单元简单，多个基本单元可扩展为非常复杂的非线性函数。因此易于构建，同时模型有很强的表达能力。
- 训练和测试的计算并行性非常好，有利于在分布式系统上的应用。
- 模型构建来源于对人脑的仿生，话题丰富，各种领域的研究人员都有兴趣，都能做贡献。
劣势：
- 数学不漂亮，优化算法只能获得局部极值，算法性能与初始值有关。
- 不可解释。训练神经网络获得的参数与实际任务的关联性非常模糊。
- 模型可调整的参数很多 （网络层数、每层神经元个数、非线性函数、学习率、优化方法、终止条件等等），使得训练神经网络变成了一门“艺术”。
- 如果要训练相对复杂的网络，需要大量的训练样本。

模型：

\begin{matrix}
a_1 = w_{11}x_1 + w_{12}x_2 + b_1 \\
a_2 = w_{21}x_1 + w_{22}x_2 + b_2 \\
z_1 = φ(a_1) \\
z_2 = φ(a_2) \\
y = w_1z_1+w_2z_2+b_3
\end{matrix}

其中，是一个非线性函数。

如果没有函数的映射，有：

y = [w_{1}w_{11}+w_{2}w_{21}]x_1+[w_{2}w_{12}+w_{2}w_{22}]x_2+[w_1b_1+w_2b_2+b_3]

这与单一神经元没有区别

非线性的激活函数：

φ(x)=\epsilon(x)=
\begin{cases}
  1 &{x>0,}  \\
  0 &{x<0.}
\end{cases}

后向传播算法（Back Propagation，BP）

https://www.zhihu.com/question/27239198

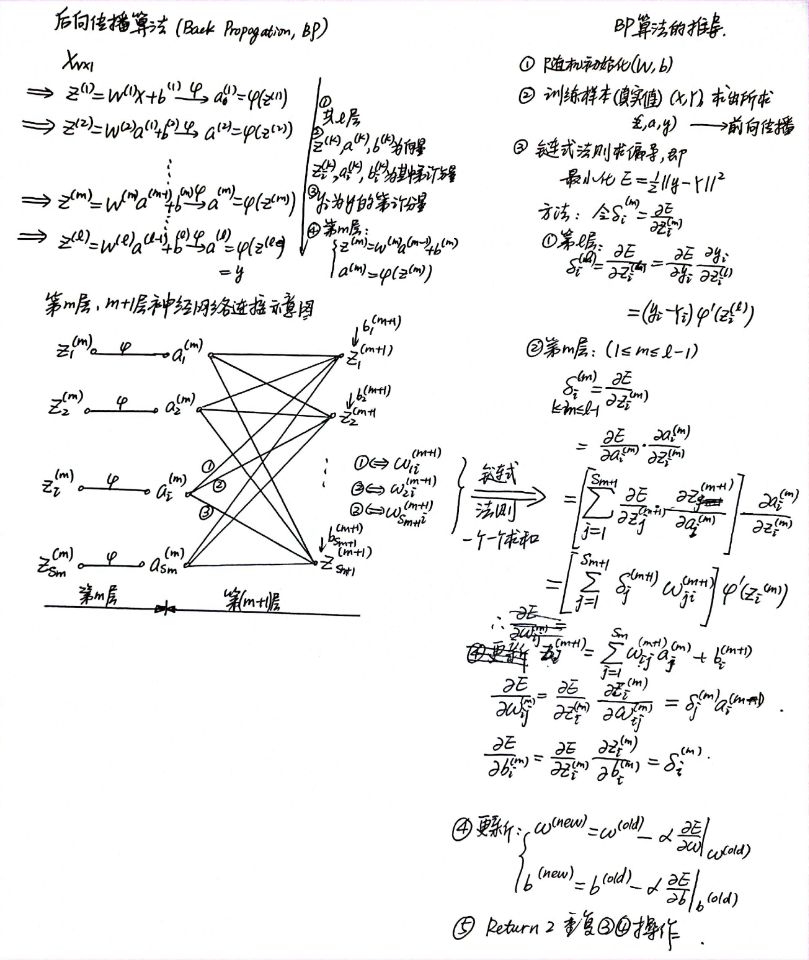
参数设置

1. 随机梯度下降

不用每输入一个样本就去变换参数，而是输入一批样本（叫做一个BATCH或MINI-BATCH），求出这些样本的梯度平均值后，根据这个平均值改变参数。（就是不像前面那样一个一个地训练，每次花费时间太长）
在神经网络训练中，BATCH的样本数大致设置为500-2000不等。

2. 激活函数选择

Sigmoid 函数（Logistic）

f(x)=\frac{1}{1+e^{-x}}

tanh 函数

f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}

ReLu 函数（深度学习）

f(x)=\max\{0,x\}

3. 训练数据初始化建议

建议：做均值和方差归一化（SVM的课后训练里面也有这一个算法）

X_{new}=\frac{X-X_{mean}}{X_{std}}

4. 初始化方法

梯度消失现象： 如果一开始很大或很小，那么梯度将趋近于0，反向传播后前面与之相关的梯度也趋近于0，导致训练缓慢。因此，我们要使一开始在零附近。（如果所有的都在0附近，由于激活函数在0附近导数的变化率很小，近似线性，破坏了神经网络的非线性优势）
一种比较简单有效的方法是：初始化从区间均匀随机取值。其中为所在层的神经元个数。可以证明，如果X服从正态分布，均值0，方差1，且各个维度无关，而是的均匀分布，则是均值为0，方差为的正态分布

5. Batch Normalization

论文： Batch normalization accelerating deep network training by reducing internal covariate shift (2015)（至2021年2月10日，引用次数为24753）
基本思想： 既然我们希望每一层获得的值都在0附近，从而避免梯度消失现象，那么我们为什么不直接把每一层的值做基于均值和方差的归一化呢？

算法如下：

Input: Values of over a mini-batch: ; Parameters to be learned:
Output:

计算方法：

\hat {x}_i \leftarrow \frac{x_i-μ_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^2+\epsilon}} \tag{BN-1}

y_i\leftarrow\gamma\hat {x}_i +\beta \equiv \mathrm{BN}_{γ,β}(x_i)\tag{BN-2}

式中，为mini-batch统计量均值，为mini-batch统计量方差

反向传播时，与原来的算法相似，据表达式有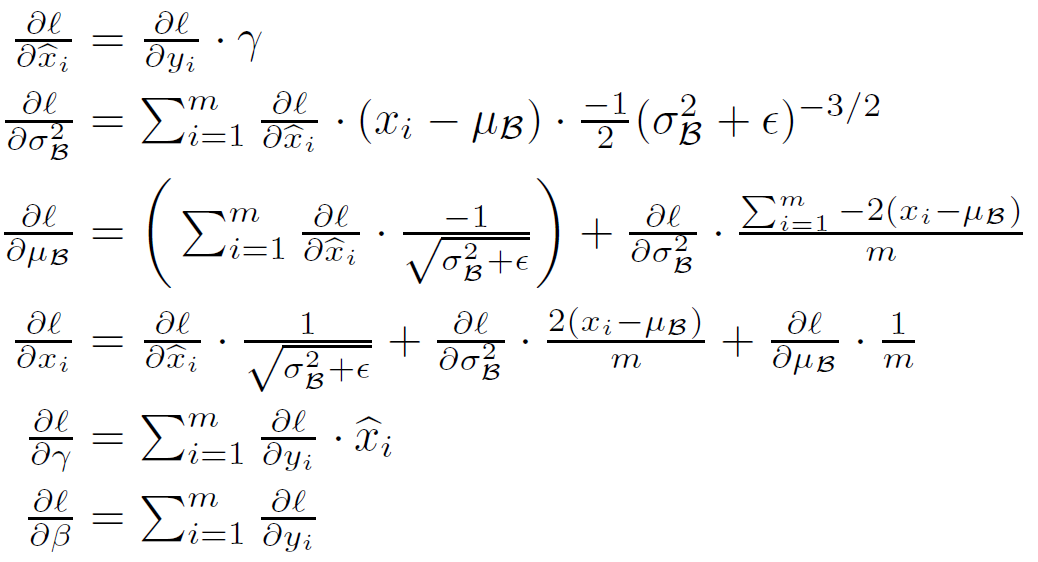：式中，为损失函数（loss function）
注：在训练的最后一个epoch时，要对这一epoch所有的训练样本的均值和标准差进行统计，这样在一张测试图片进来时，使用 训练样本中的标准差的期望 和 均值的期望 对测试数据进行归一化，注意这里标准差使用的期望是其无偏估计：
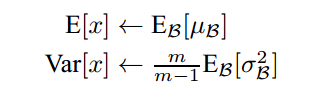
经过试验，发现Batch Normalization后，学习率的参数选择对最终结果影响比较小

6. 目标函数objective function选择基本概念

Method 1：可加正则项 Regular Term

L(W)=F(W)+R(W)=\frac{1}{2}\left(\sum_{i=1}^{batch\_size}||y_i-Y_i||^2+\beta\sum_k{\sum_l W_{k,l}^2}\right)

和SVM中使用的正则项一样，此处的正则项也是用于防止出现训练的过拟合。

Method 2：如果是分类问题，可以采用SOFTMAX函数和交叉熵损失函数的组合。 （图在文末）

Softmax 假设一个样本有层，且第层输出有N个概率（分为N类，每一个通过神经网络的值为），那么定义一个Softmax，其映射关系如下函数所示：
```
q_i=\frac{\exp{z_i}}{\sum_{j=1}^N\exp{z_j}}
```
Advantages
- Able to handle multiple classes only one class in other activation functions—normalizes the outputs for each class between 0 and 1, and divides by their sum, giving the probability of the input value being in a specific class.
- Useful for output neurons—typically Softmax is used only for the output layer, for neural networks that need to classify inputs into multiple categories.
强行把输出的值变成概率，应用举例：某一张图片被识别为猫的概率为60%，被识别为狗的概率为40% 另外设定一个向量为目标概率，目的是使及其学习这一进程。此时产生的误差（MSE Mean Square Error）为
```
\mathrm{MSE}=\frac{1}{2}||q-p||^2
```
交叉熵（Cross Entropy）损失函数
- 交叉熵简介
- 定义：
```
E=-\sum_{i=1}^N p_i\log{q_i}
```
- 若是SOFTMAX函数和交叉熵的组合，则有结论
```
\frac{\partial E}{\partial {z_i}}=q_i-p_i
```

7. 学习率的调节 （不同的梯度下降算法Click Here）

传统方法：
- 常规的更新（Vanilla Stochastic Gradient Descent）——固定步长，靠经验分析（传统方法通常用小批量梯度下降）
  - SGD的问题
    - (W,b)的每一个分量获得的梯度绝对值有大有小，一些情况下，将会迫使优化路径变成Z字形状。
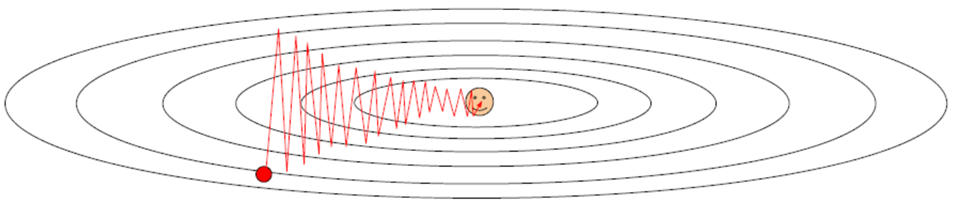
    - SGD求梯度的策略过于随机，由于上一次和下一次用的是完全不同的BATCH数据，将会出现优化的方向随机的情况。
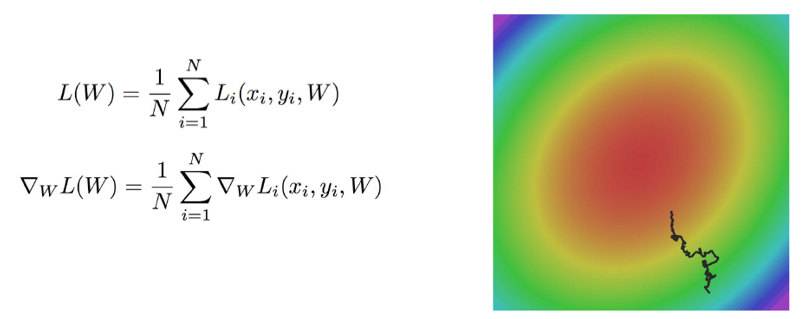
提出方案：AdaGrad RMSProp Momentum 等等，搜寻资料建议直接上慕课公开课或者查阅文献，不建议百度知乎。

训练建议

一般情况下，在训练集上的损失函数的平均值（cost）会随着训练的深入而不断减小，如果这个指标有增大情况，停下来。有两种情况：第一是采用的模型不够复杂，以致于不能在训练集上完全拟合；第二是已经训练很好了。
分出一些验证集（Validation Set）,训练的本质目标是在验证集上获取最大的识别率。因此训练一段时间后，必须在验证集上测试识别率，保存使验证集上识别率最大的模型参数，作为最后结果。
注意调整学习率（Learning Rate），如果刚训练几步目标函数cost就增加，一般来说是学习率太高了；如果每次目标函数cost变化很小，说明学习率太低。
Batch Normalization比较好用，用了这个后，对学习率、参数更新策略等不敏感。
如果不用Batch Normalization, 合理变换其他参数组合，也可以达到目的。
由于梯度累积效应，AdaGrad RMSProp Adam三种更新策略到了训练的后期会很慢，可以采用提高学习率的策略来补偿这一效应。

基于以上分析，多层神经网络（以两层为例）的图示如下： Source

本文章使用limfx的vscode插件快速发布

神经网络 简介