求解O-S方程的过程(1)布拉休斯解

对于O-S方程，没有封闭形式的解的存在，但是可以求解简化后的O-S方程，获得扰动的速度场，然后将扰动速度场作为初值，再进行迭代。所以首先我们要讨论一下简化的O-S方程：

原始的O-S方程为：

(U-c)(\phi^{\prime}-\alpha^2\phi)-U^{\prime \prime}\phi=-\frac{i}{\alpha Re}(\phi^{\prime \prime \prime\prime}-2\alpha^2\phi^{\prime\prime}+\alpha^{4}\phi)

在边界层外，速度将会趋于一个常数，也就是说,简化之后，得到简化版O-S方程：

\phi^{\prime\prime\prime\prime}-(\alpha^2+\gamma^2)\phi^{\prime\prime}+\alpha^{2}\gamma^{2}\phi=0

其中,。那么作为一个常微分方程，简化后的O-S方程由四个指数函数表示的通解：

其中，由于是波数显然是大于0的，而的实部也是大于零的。那么当时，方程解要保持有界，则只有是有效的解，从物理方面理解，作为扰动速度的流函数，传向远场时应该是趋于0的。

因此只有满足O-S方程在边界层外的解，当时，方程的通解可以由表示。

那么我们就可以用作为O-S方程作为O-S方程的初值，采用Runge-Kutta法进行数值迭代，找到最合适的解。

这里先对怎么数值迭代按下不表，首先要讨论一下解的过程。首先一开始，解是线性无关的，但是随着数值迭代的进行，线性无关性会很快消失，那么这是为什么呢？

这个问题主要是处在电脑上表示数据所带来的舍入误差，毕竟计算机上的数值再怎么精确表示一个数，总是会有精度的损失。

假设精度的损失为,我们只考虑对于，当我们从边界层外向内积分一步时：

\phi(y-h)=c_1\pm\epsilon

那么当下一步从到积分时，舍入误差给出了一个获得解的合适初始条件，也就是说，在这一步的迭代后的解是,两个解的组合，不再是单独的用表示的结果了，即，这次由于在每次积分是，微分方程都会接受更一般的解，比如说基于而不是基于。在这里面，。

然后对于和，可以发现随着y的变化，的增长率要远大于，所以如果积分过程足够长，那么由开始的解会被所主导，因此解也就失去了线性无关的性质。而的增长率随着雷诺数的增大而怎大，所以不可避免的，在高雷诺数下，的解就会被所污染。这一困难能够通过应用精确的算术方法解决，但需要耗费编程者大量的精力以及计算所花的时间。因此，对于太长的计算时间，是直接的结果皆被限制在了低马赫数上。

但在文献中，说明了一种进行精确迭代的办法。以Runge-Kutta法迭代10步，每步为0.01为例。当我们从边界层外向下推进时，会获得解，还有他们的舍入误差。接下来，我们进行施密特正交化，将两个解向量,转化为新的正交解向量,,其中，

\overline{\phi}_3(0.90)=\frac{\phi_3(0.90)}{|\phi_3(0.90)|}\\
\overline{\phi}_1(0.90)=\frac{\phi_1(0.90)-(\phi_1(0.90),\overline{\phi}_3(0.90))\overline{\phi}_3(0.90)}{{\phi}_1(0.90)-(\phi_1(0.90),\overline{\phi}_3(0.90))\overline{\phi}_3(0.90)}

现在我们可以使用y=0.90时的新的解,通过把O-S方程从y=0.90积分到0.80，通过这种方式，我们可以求解O-S方程直到时仍然保持有两个正交向量。

当然，通过这种方式求解O-S方程，需要先知道边界层的速度场，这有布拉休斯解提供的速度场。

如何使用C++求布拉休斯解

参考网络上的布拉休斯解求解方法

ff^{\prime\prime}+2f^{\prime\prime\prime}=0;\\
f(0)=f^\prime(0)=0;f^{\prime\prime}=1

引入新的变量

，那么布拉休斯方程可以等价的表示为：

\left\{\begin{array}{l}
y_{n+1}=y_{n}+\frac{h}{6}\left(K_{1}+2 K_{2}+2 K_{3}+K_{4}\right) \\
K_{1}=f\left(x_{n}, y_{n}\right) \\
K_{2}=f\left(x_{n}+\frac{h}{2}, y_{n}+\frac{h}{2} K_{1}\right) \\
K_{3}=f\left(x_{n}+\frac{h}{2}, y_{n}+\frac{h}{2} K_{2}\right) \\
K_{4}=f\left(x_{n}+h, y_{n}+h K_{3}\right)
\end{array}\right.

对于y1：

\left\{\begin{array}{l}
y_{1}^{n+1}=y_{1}^{n}+\frac{h}{6}\left(K_{11}+2 K_{12}+2 K_{13}+K_{14}\right) \\
K_{11}=y_{2}^{n} \\
K_{12}=y_{2}^{n}+\frac{h}{2} K_{11} \\
K_{13}=y_{2}^{n}+\frac{h}{2} K_{12} \\
K_{14}=y_{2}^{n}+h K_{13}
\end{array}\right.

y2与y1几乎一样，只是把y1中的y2改为y3即可：

\left\{\begin{array}{l}
y_{2}^{n+1}=y_{2}^{n}+\frac{h}{6}\left(K_{21}+2 K_{22}+2 K_{23}+K_{24}\right) \\
K_{21}=y_{3}^{n} \\
K_{22}=y_{3}^{n}+\frac{h}{2} K_{21} \\
K_{23}=y_{3}^{n}+\frac{h}{2} K_{22} \\
K_{24}=y_{3}^{n}+h K_{23}
\end{array}\right.

而对于y3，则需要额外注意：

\left\{\begin{array}{l}
y_{2}^{n+1}=y_{2}^{n}+\frac{h}{6}\left(K_{21}+2 K_{22}+2 K_{23}+K_{24}\right) \\
K_{21}=y_{3}^{n} \\
K_{22}=y_{3}^{n}+\frac{h}{2} K_{21} \\
K_{23}=y_{3}^{n}+\frac{h}{2} K_{22} \\
K_{24}=y_{3}^{n}+h K_{23}
\end{array}\right.

对于这部分，可以使用C++的函数重载功能定义，最后的结果如下：

//main.cc
#include <iostream>
#include <new>
#include <fstream>
#include "RK4.h"
using namespace std;

int main()
{
    double boundaryLength = 10;
    int stepNumber = 1000;
    RungeKutta y1(boundaryLength,stepNumber);
    y1.writeForTecplot(y1.Calculate(1.0,1e-9));
    return 0;
}

//RK4.h
class RungeKutta
{
    public:
    double yIter0,yIter1,boundaryLength;
    int stepNumber;
    double (*y)[3];
    public:
    explicit RungeKutta(double,int);
    double Iter(double,double);
    double Iter(double,double ,double,double);
    double  **Calculate(double,double);
    void writeForTecplot(double **);
};

//RK4.cc
#include "RK4.h"
#include <cmath>
#include <fstream>
#include <iomanip>
#include <cstring>
using namespace std;
RungeKutta::RungeKutta(double a, int b) : boundaryLength(a), stepNumber(b) {}
double RungeKutta::Iter(double yIter0, double fdiff)
{
        double h = boundaryLength / stepNumber;
        double K1, K2, K3, K4;
        K1 = fdiff;
        K2 = fdiff + 0.5 * h * K1;
        K3 = fdiff + 0.5 * h * K2;
        K4 = fdiff + h * K3;
        yIter1 = yIter0 + h / 6.0 * (K1 + 2 * K2 + 2 * K3 + K4);
        return yIter1;
}
double RungeKutta::Iter(double yIter0, double coef, double fdiffx, double fdiffy)
{
        double h = boundaryLength / stepNumber;
        double K1, K2, K3, K4;
        K1 = coef * fdiffx * fdiffy;
        K2 = coef * (fdiffx + 0.5 * h * K1) * (fdiffy + 0.5 * h * K1);
        K3 = coef * (fdiffx + 0.5 * h * K2) * (fdiffy + 0.5 * h * K2);
        K4 = coef * (fdiffx + h * K1) * (fdiffy + h * K1);
        yIter1 = yIter0 + h / 6.0 * (K1 + 2 * K2 + 2 * K3 + K4);
        return yIter1;
}


double **RungeKutta::Calculate(double y3Init, double errorValue)
{
        double h = boundaryLength / stepNumber;
        double **y;
        double error = 1;
        y = (double **)malloc(stepNumber * sizeof(double *));
        for (int i = 0; i < stepNumber; i++)
        {
                y[i] = (double *)malloc(3 * sizeof(double));
        }
        memset(*y, 0, sizeof(double) * stepNumber * 3);
        y[0][2] = y3Init;
        while (error >= errorValue)
        {
                for (int i = 0; i < (stepNumber - 1); i++)
                {
                        y[i + 1][0] = RungeKutta::Iter(y[i][0], y[i][1]);
                        y[i + 1][1] = RungeKutta::Iter(y[i][1], y[i][2]);
                        y[i + 1][2] = RungeKutta::Iter(y[i][2], -0.5, y[i][0], y[i][2]);
                }
                error = fabs(y[stepNumber - 1][1] - 1);
                y[0][2] -= 0.3 * error;
        }
        return y;
}
void RungeKutta::writeForTecplot(double **y)
{
        int charwidth = 20;
        double h = boundaryLength / stepNumber;
        ofstream file("blauis.dat");
        if (file.is_open())
        {
                file << "variables=\"y\" \"f\" \"f1\" \"f2\"" << endl;
                file << "ZONE t=\"blauis\" \nI=" << stepNumber << ",F=POINT" << endl;
                for (int i = 0; i < stepNumber; i++)
                {
                        file << (h * i) << setw(charwidth) << y[i][0] << setw(charwidth) << y[i][1] << setw(charwidth) << y[i][2] << endl;
                }
        }
        file.close();
}

运行之后，会生成一个Tecplot文件，导入之后可以得到结果，如下图所示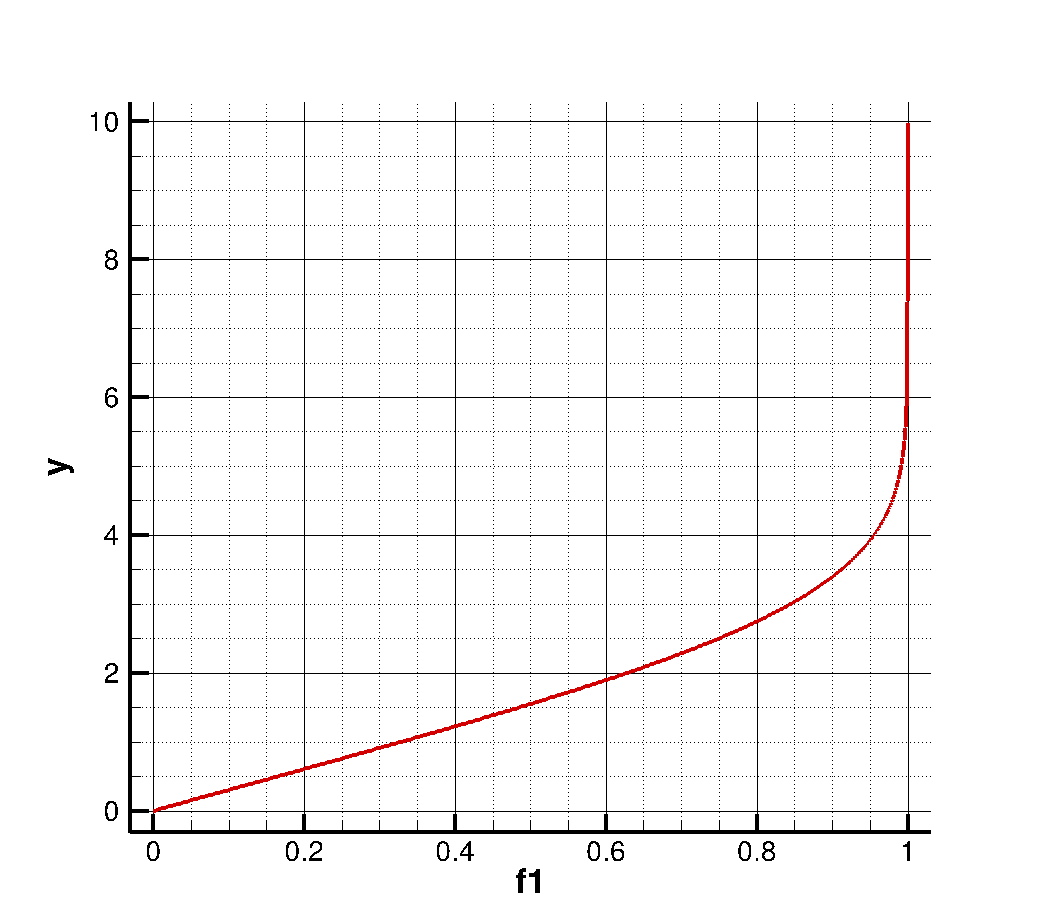：布拉休斯解

本文章使用limfx的vscode插件快速发布