MATLAB 二次规划和整数规划

二次规划

若某非线性规划的目标函数为自变量 x 的二次函数，约束条件又全是线性的，就称这种规划为二次规划。

\[ min \frac{1}{2}x^THx+f^Tx\\ s.t.\quad Ax \leq b \]

quadprog函数

\[ [x,fval]=quadprog(H,f,A,b,Aeq,beq,LB,UB,X0) \]

• H、f 即目标函数中的 H、f

• 其他参数与线性规划相同，参见线性规划

• 二次规划所求的结果为精确最优解

实例

\[ minf(x)=2x_1^2-4x_1x_2+4x_2^2-6x_1-3x_2\\ s.t.\begin{cases} x_1+x_2 \leq3\\ 4x_1+x_2\leq 9\\ x_1,x_2\geq 0 \end{cases} \]

h = [4,-4;-4,8];
f = [-6;-3];
a = [1,1;4,1];
b = [3;9];
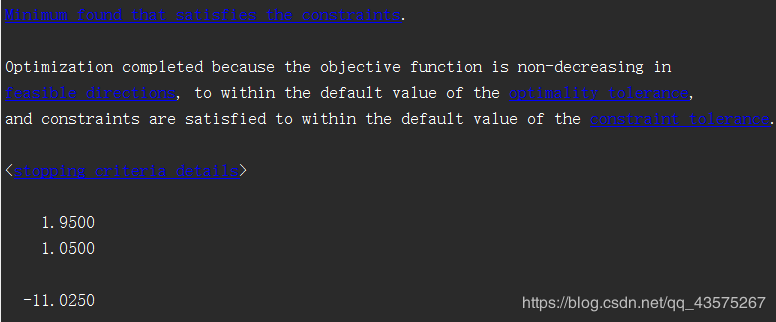
[x,fval] = quadprog(h,f,a,b,[],[],zeros(2,1));
disp(x)
disp(fval)

整数规划

规划中的变量限制为整数时，称为整数规划。

intlinprog函数

\[ [x,fval]=intlinpog(c,intcon,A,b,Aeq,beq,LB,UB) \]

• intcon 是只能取整数的自变量序号

• 没有被 intcon 限定的自变量可以不必是整数；被 intcon 限定的自变量也可以有上下界

• 其他参数与线性规划相同

实例

\[ minz=-3x_1-2x_2-x_3\\ s.t.\begin{cases} x_3 \quad int\\ x_1,x_2 \geq 0\\ x_1+x_2+x_3 \leq 7\\ 4x_1+2x_2+x_3 = 12 \end{cases} \]

clear
c = [-3;-2;-1];
intcon = 3;
A = [1 1 1];
b = 7;
Aeq = [4 2 1];
beq = 12;
[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,[0;0;0]);
disp(x)
disp(fval);

说明

在建模过程中，遇到线性规划、整数规划、二次规划问题，只需要根据条件一步步列写约束方程和目标方程，写成标准的形式。然后直接用 matlab 获得结果。以上三种规划都能获得全局最优解。

---

本文章使用limfx的vsocde插件快速发布