指标
1、问题与数据
某研究者为评价胸部门诊对乳腺癌患者的诊断价值，以最终手术病理结果为金标准，选择100位患者和900位非患者进行胸部扪诊。胸部扪诊的结果为180例阳性，820例阴性，具体如下：
胸部扪诊/手术病理结果 | 患者 | 非患者 | 合计 |
|---|---|---|---|
阳性 | 80 | 100 | 180 |
阴性 | 20 | 800 | 820 |
合计 | 100 | 900 | 1000 |
问题：胸部扪诊对乳腺癌患者的诊断价值如何？
2、问题的分析
胸部扪诊的结局变量是2分类的，只有阳性和阴性结果。胸部扪诊评价乳腺癌会出现以下4种具体的情况：
诊断试验/金标准 | 患者 | 非患者 |
|---|---|---|
阳性 | 真阳性TP(A) | 假阳性FP(B)没病但试验阳性(误检) |
阴性 | 假阴性FN(C) 有病但试验阴性(漏检) | 真阴性TN(D) |
研究发现，100例金标准确认的患者中，胸部扪诊仅发现80例患者（真阳性），而另外20例没有发现（假阴性）。同时，900例金标准确认的非患者中，胸部扪诊仅发现800例非患者（真阴性），而另外100例被错误的认为是患者（假阳性）
要评价胸部扪诊结果的真实性，可以应用灵敏度、特异度等指标。
3、评价方法
3.1 灵敏度
该研究中，根据手术病理结果有100例乳腺癌患者，但胸部扪诊只检测出其中80例患者。这说明该诊断试验只能发现80%的病人。即，该诊断试验的灵敏度为：
Sensitivity=灵敏度=\frac{TP}{TP+FN}=\frac{真阳性}{真阳性+假阴性}=\frac{80}{80+20}*100\%=80\%
灵敏度（sensitivity），又称真阳性率，即实际有病，并且按照该诊断试验的标准被正确地判为有病的百分比。它反映了诊断试验发现病人的能力。
3.2 特异度
在这项研究中，有900例不是乳腺癌患者，但胸部扪诊只识别了其中的800例。即，该诊断试验的特异度为：
Specificity=特异度=\frac{TN}{TN+FP}=\frac{真阴性}{真阴性+假阳性}=\frac{800}{800+100}*100\%\approx89\%
特异度（specificity），又称真阴性率，即实际没病，同时被诊断试验正确地判为无病的百分比。它反映了诊断试验确定非病人的能力。
3.3 灵敏度和特异度指标的重要性
如果一项诊断试验的灵敏度比较低（漏检），那么会出现很多假阴性的患者。这会延误患者的就诊，影响病程发展和愈后，甚至导致患者过早死亡。
如果一项诊断试验的特异度比较低(误诊)，那么会出现很多假阳性的患者。这样会浪费医疗资源、造成患者无端的恐慌和焦虑。
3.4 准确度
准确率(Accuracy)是指预测正确的样本占总样本的比例，即模型找到的真正类与真负类与整体预测样本的比例。用公式表示为：
Accuracy=\frac{TP+TN}{TP+TN+FP+FN}=\frac{80+800}{80+800+100+20}*100\%=88\%
3.5 精确率(查准率)与召回率(查全率)
精确率(Precision)和召回率(Recall)是一对好兄弟，虽然是两个不同的评价指标，但它们互相影响，通常一起出现。在很多书上又把精确率称为查准率，把召回率称为查全率。
Precision=精确率=查准率=\frac{TP}{TP+FP}=\frac{真阳性}{真阳性+假阳性}
精确率是针对预测结果而言的指标，它表示预测为正类的样本中有多少是对的
Recall=召回率=查全率=\frac{TP}{TP+FN}=\frac{真阳性}{真阳性+假阴性}
召回率是针对原始样本而言的指标，它表示原始样本中的正例有多少被预测正确
相比准确率而言，召回率更真实地反应了模型的效果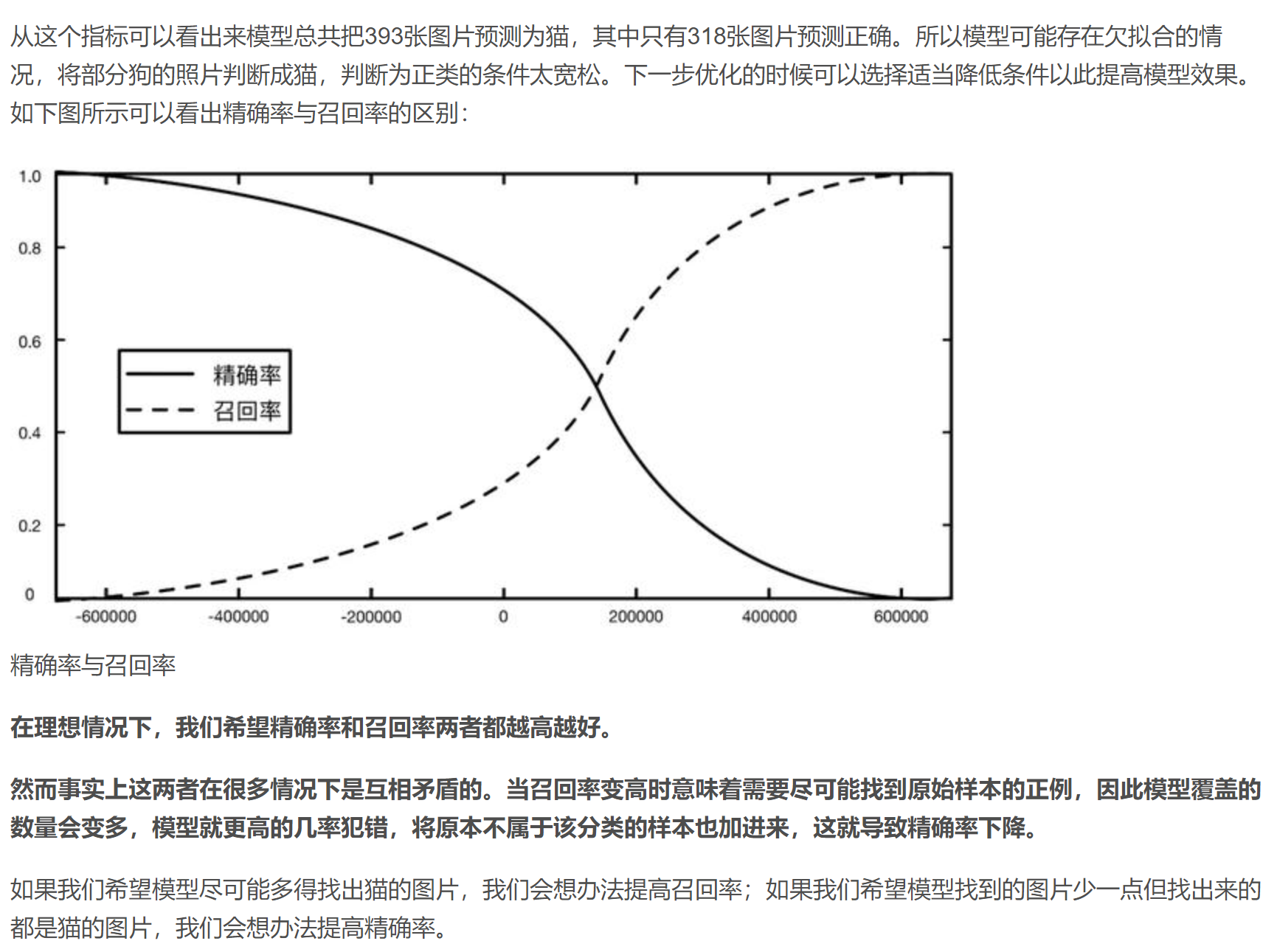 
3.6 ROC曲线
在逻辑回归的分类模型里，对于正负例的界定，通常会设一个阈值。大于阈值的样本判定为正类，小于阈值的样本为负类。如果我们减小这个阈值，会让更多的样本被识别为正类，从而提高了正类的识别率，但同时也会使得更多的负类被错误识别为正类。
直接调整阈值可以提升或降低模型的精确率和召回率，也就是说使用精确率和召回率这对指标进行评价时会使得模型多了“阈值”这样一个超参数，并且这个超参数会直接影响模型的泛化能力。在数学上正好存在ROC曲线能够帮助我们形象化地展示这个变化过程
ROC曲线是一个画在二维平面上的曲线，平面的横坐标是假正类率(FalsePositive Rate，简称FPR)，计算公式为：
FPR=假正类率=\frac{FP}{FP+TN}=\frac{假正类}{假正类+真负类}
纵坐标是真正类率(True Positive Rate，简称TPR)，计算公式为：
TPR=真正类率=\frac{TP}{TP+FN}=\frac{真正类}{真正类+假负类}
对于一个分类器而言，每一个阈值下都会有一个FPR和TPR，这个分类器就可以映射成ROC平面上的一个点。当我们调整这个分类器分类时使用的阈值，就可以得到一个经过(0,0)，(1, 1)的曲线，这条曲线就是这个分类器的ROC曲线，如下图所示。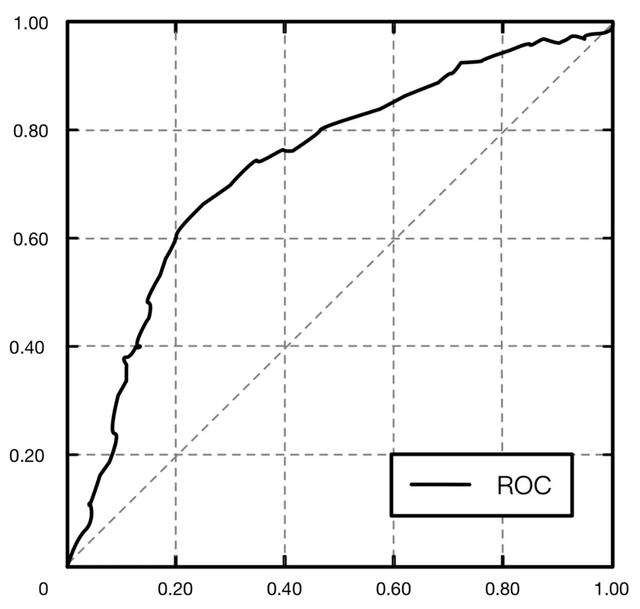 
从图中可以看到，所有算法的ROC曲线都在y=x这条线的上方，因为y=x表示了随机的猜测的概率。所有二分类问题随便猜正确或不正确都是50%的准确率。
一般情况下不存在比随机猜测的准确率更糟糕的算法，因为我们总是可以将错误率转换为正确率。如果一个分类器的准确率是40%，那么将两类的标签互换，准确率就变为了60%。
从图中可以看出来，最理想的分类器是到达(0,1)点的折线，代表模型的准确率达到100%，但是这种情况在现实中是不存在的。如果我们说一个分类器A比分类器B好，实际上我们指的是A的ROC曲线能够完全覆盖B的ROC曲线。如果有交点，只能说明A在某个场合优于B，如下图所示。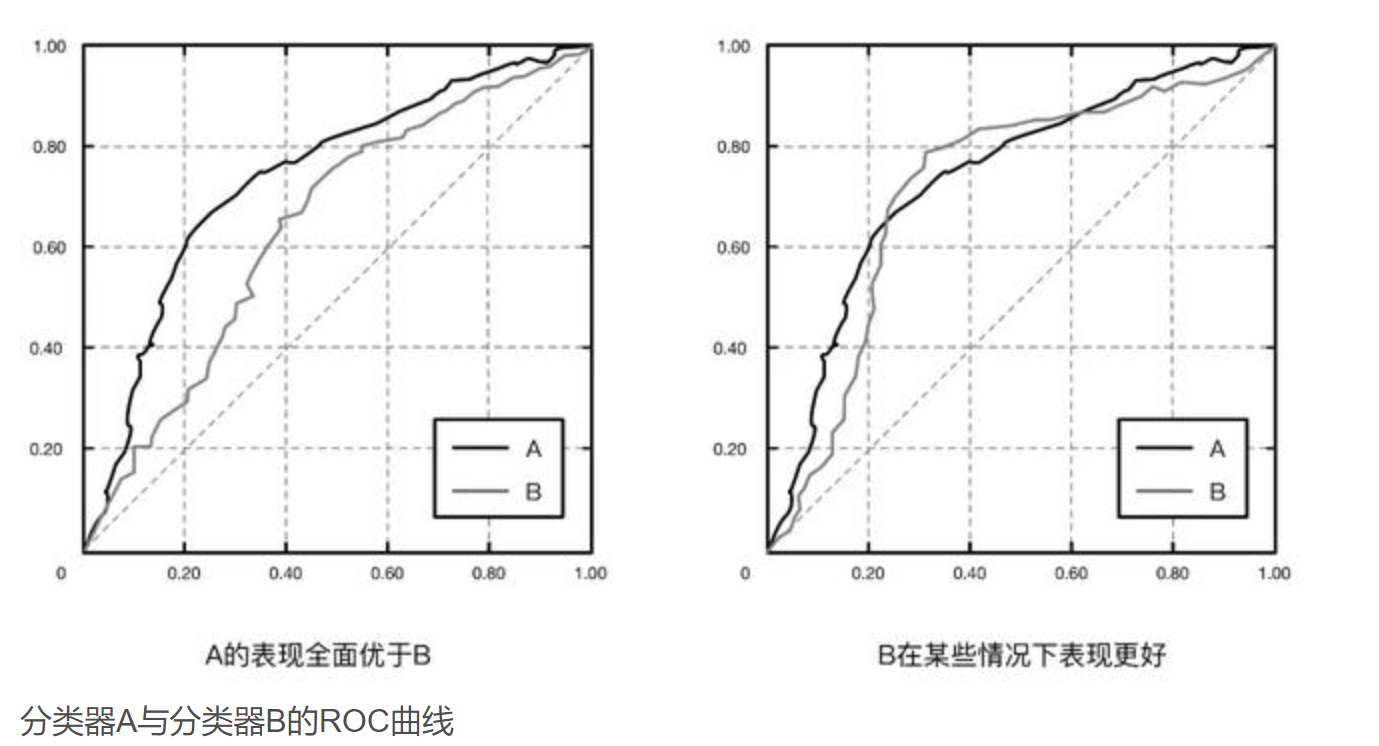 
3.7 AUC值
ROC曲线一定程度上可以反映分类器的分类效果，但始终是以图像的形式，不能告诉我们直接的结果。我们希望有一个指标，这个指标越大代表模型的效果越好，越小代表模型的效果越差。于是引入了AUC值(Area Under Curve)的概念。
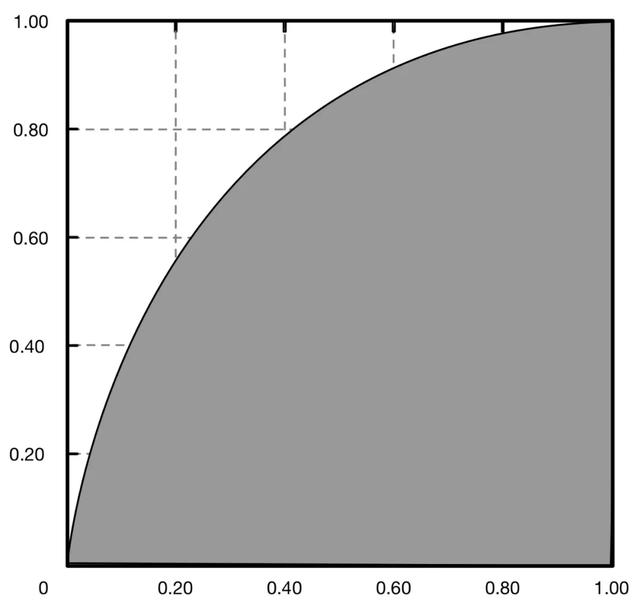
AUC是数据分析中最常用的模型评价指标之一，实际上AUC代表的含义就是ROC曲线下的面积，如下图所示，它直观地反映了ROC曲线表达的分类能力。AUC值通常大于0.5小于1，AUC(面积)越大的分类器，性能越好。
本文章使用limfx的vscode插件快速发布