实验1《递归与分治策略》

《算法设计与分析》实验报告

实验一递归与分治策略

报告书
姓名	xxx	指导教师	李纲
学号	1 96001736	日期	2 022.3.8
班级	1 9 计算机1班
实验内容
[要求先在OJ上提交通过] 1、[OJ]递推/递归与分治策略1 2、[OJ]递推/递归与分治策略2 3、[OJ]递推/ 递归与分治策略-堂练
实验目的
1）请补充完整；如掌握什么知识点等 2）学习掌握本类算法的设计与实现，在OJ上提交算法代码并测试通过，完成实验报告书写。
【如有查重雷同，请在此说明】
代码独立完成，无雷同。
【如有OJ未完成，请在此说明，并在本实验文档中补全】
OJ实验1作业正常时间完成。 OJ实验2作业正常时间完成。 OJ实验3堂练未全部完成：题号，已在报告中补全
实验过程和步骤
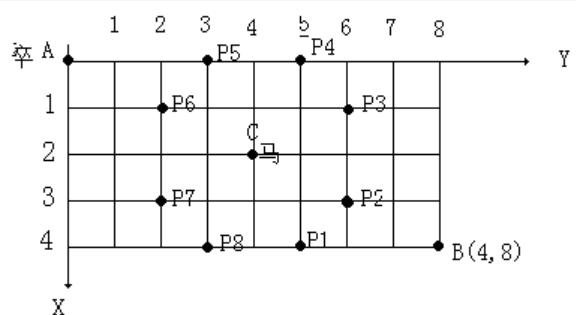
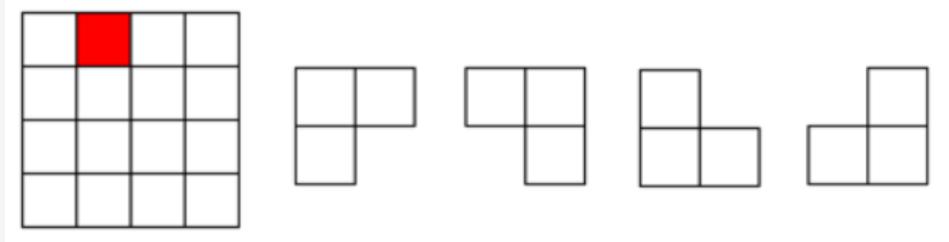
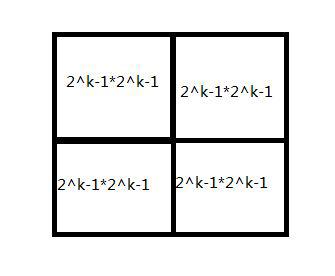
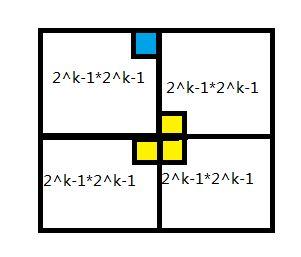
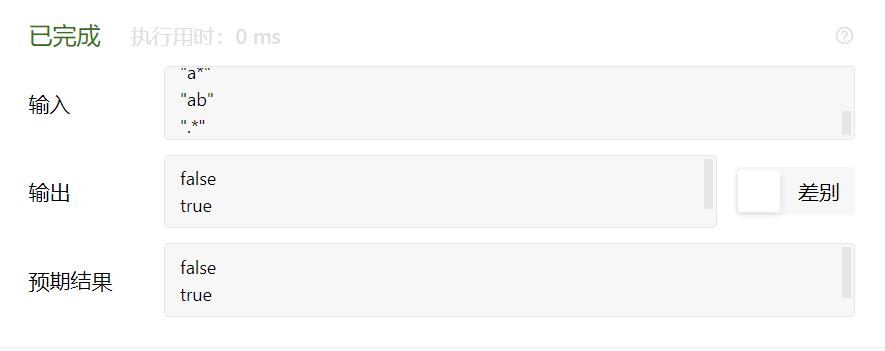
【第一部分/90分】  递推/递归与分治策略1 1 -0 ：实验题目：王老师爬楼梯题目描述：王老师爬楼梯，他可以每次走1级或者2级或者3级楼梯，输入楼梯的级数，求不同的走法数。（要求递推求解）如果N很大，需要高精度计算。输入要求：一个整数N，N<=1000。输出要求：共有多少种走法。实验代码及注释: 定义大数类，实现大数的算数操作以及输入输出，大数类BigInterger的定义见附录所示。主体代码： bool flag [ 1001 ] = { false }; //定义标记数组，就第i个数是否被计算过 BigInteger num [ 1001 ]; // 记录被计算过的数 BigInteger f ( int n ) { if ( n == 0 ) //递归边界 { if ( flag [ n ]) return num [ n ]; else { flag [ n ] = true ; num [ n ] = 1 ; return num [ n ]; } } else if ( n == 1 ) //递归边界 { if ( flag [ n ]) return num [ n ]; else { flag [ n ] = true ; num [ n ] = 1 ; return num [ n ]; } } else if ( n == 2 ) //递归边界 { if ( flag [ n ]) return num [ n ]; else { flag [ n ] = true ; num [ n ] = 2 ; return num [ n ]; } } else { if ( flag [ n ]) { return num [ n ]; } else //递归条件 { num [ n ] = f ( n - 1 ) + f ( n - 2 ) + f ( n - 3 ); flag [ n ] = true ; return num [ n ]; } } } int main () { BigInteger res ; int n ; cin >> n ; res = f ( n ); //调用函数获取王老师的爬楼梯方法数 cout << res << endl ; return 0 ; } OJ提交截图及遇到的问题第一次Time Limit Exceeded是因为没有对递归过程中产生的中间数据进行优化，每次都是要重复计算，导致有大量冗余重复的计算导致超时。算法分析与知识点：本题主要涉及大数运算以及递归的应用，递归需要分析递归的条件，本题的递归条件为考虑王老师最后一次跨几步可分为最后跨一步、最后跨两步和最后跨三步三种得出。 1 -1 ：实验题目：铺砖题目描述：对于一个2行N列的走道。现在用12或22的砖去铺满。问有多少种不同的方式（请用递推方式求解）。如果N很大，需要高精度计算。下图是一个2行17列的走道的某种铺法：输入要求：一个整数N，N<=1000。输出要求：共有多少种铺法。实验代码及注释: 大数类BigInterger的定义与上题相同。 bool flag [ 1001 ] = { false }; //定义标记数组，就第i个数是否被计算过 BigInteger num [ 1001 ]; // 记录被计算过的数 BigInteger f ( int n ) { if ( n == 1 ) //递归边界 { if ( flag [ n ]) //判断第i个数是否被计算过 return num [ n ]; else { flag [ n ] = true ; num [ n ] = 1 ; return num [ n ]; } } else if ( n == 2 ) //递归边界 { if ( flag [ n ]) //判断第i个数是否被计算过 return num [ n ]; else { flag [ n ] = true ; num [ n ] = 3 ; return num [ n ]; } } else { //递归条件 if ( flag [ n ]) //判断第i个数是否被计算过 { return num [ n ]; } else { num [ n ] = f ( n - 1 ) + f ( n - 2 ) + f ( n - 2 ); flag [ n ] = true ; return num [ n ]; } } } int main () { BigInteger res ; int n ; cin >> n ; res = f ( n ); //调用函数获取总铺砖方法数 cout << res << endl ; return 0 ; } OJ提交截图及遇到的问题第一次Time Limit Exceeded是因为将递归条件写成了而乘法相对于加法而言会耗费更多的时间从而导致了超时。将递归条件改为就AC通过了。算法分析与知识点：本题主要涉及大数运算以及递归的应用，递归需要分析递归的条件，本题的递归条件为考虑铺砖最后一次剩几列可分为最后剩一列和最后剩两列两种，剩两列又可分为 22 和2个1 2 ，最终得出。  递推/递归与分治策略 2 2-0 ：实验题目：第K小的数题目描述：输入n个数，求其中第k小的数。（要求采用分治法完成，不建议采用完整的排序）输入要求：第一行包含两个整数n和k；n<1000，1<=K<=n 第二行包含n个整数。输出要求：输出第k小的那个整数。实验代码及注释: #include <bits/stdc++.h> using namespace std ; int f ( vector < int > data , int k ) { //定义寻找第k小的函数 int pop_size = data . size (); //获取要寻找数组的大小 if ( pop_size < 75 ) { //确定解决问题的最小规模 sort ( data . begin (), data . end ()); return data [ k - 1 ]; } vector < int > middle ; int group_num = 5 ; //每组5个进行分治 for ( int i = 0 ; i < pop_size ; i += group_num ) { vector < int > temp ; //获取临时数据 for ( int j = i ; j < i + group_num && j < pop_size ; j ++ ) { temp . push_back ( data [ j ]); } if ( temp . size ()) middle . push_back ( f ( temp , 1 + temp . size () / 2 )); //获取每组临时数据的中位数 } int key = f ( middle , 1 + middle . size () / 2 ); //获取原来数据的中位数 vector < int > part1 , part2 ; for ( int i = 0 ; i < pop_size ; i ++ ) { if ( data [ i ] > key ) part1 . push_back ( data [ i ]); else part2 . push_back ( data [ i ]); } if ( k <= part2 . size ()) // 根据中位数的位置选取哪一部分的子区间 return f ( part2 , k ); else return f ( part1 , k - part2 . size ()); } int main () { vector < int > data ; int n , k ; cin >> n >> k ; for ( int i = 0 ; i < n ; i ++ ) { int t ; cin >> t ; data . push_back ( t ); } int ans = f ( data , k ); cout << ans << endl ; return 0 ; } OJ提交截图及遇到的问题算法分析与知识点：本题主要运用了递归分治的思想，将原问题转化为先求5个数一组的小组分别求出其中位数，最后汇总得到总数组的中位数，然后根据该数的下标与k的关系，转化为规模为原问题一半的子问题。 2-1 ：实验题目：涂格子题目描述：有排成一行的n个方格，用红、粉、绿三色涂每个格子，要求：（1）任何相邻的方格不能同色；（2）且首尾两格也不同色求n个格子满足要求的涂法数。输入要求：输入多个整数n，每个整数表示有多少个方格，n<=60 输出要求：输出多个整数，一行一个，表示每个对应输入的涂法数实验代码及注释: #include <bits/stdc++.h> using namespace std ; long long f ( int n ) { long long data [ 61 ] = { 3 , 6 , 6 }; if ( n <= 2 ) return data [ n - 1 ]; else { for ( int i = 3 ; i < n ; i ++ ) { data [ i ] = data [ i - 1 ] + 2 * data [ i - 2 ]; //递推公式 } return data [ n - 1 ]; } } int main () { int n ; while ( cin >> n ) { long long ans = f ( n ); cout << ans << endl ; } return 0 ; } OJ提交截图及遇到的问题算法分析与知识点：本题主要运用递归的思想，考虑最后一个格子与第一个格子的颜色是否相同可分为两种情况，进一步分析可得到以下关系。 2-2 ：实验题目：过河卒/noip2002 题目描述：棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下或向右。同时在棋盘上的任一点有一个对方的马(如图中的C点)，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如图中C点上的马可以控制9个点。卒不能走到对方马的控制点。棋盘用坐标表示，A点坐标(0,0)、B点坐标(n, m) (n,m为不超过20的整数,并由键盘输入),同样马的位置坐标C是需要给出的(C≠A,且C≠B)。现在要求你计算出卒从A点能够到达B点的路径条数。输入要求： B点的坐标(n, m)以及对方马的坐标（ｘ，ｙ），不用判错。输出要求：一个整数（路径的条数）。实验代码及注释: #include <bits/stdc++.h> using namespace std ; bool check ( int cx , int cy , int x , int y ) { //检查位置是否为马的控制点 if ( abs ( cx - x ) * abs ( cy - y ) == 2 \|\| ( cx == x && cy == y )) return true ; else return false ; } long long f ( int cx , int cy , int n , int m , int x , int y ) { long long map [ 21 ][ 21 ] = { 0 }; for ( int i = 0 ; i <= n ; i ++ ) { for ( int j = 0 ; j <= m ; j ++ ) { if ( i == 0 && j == 0 ) map [ i ][ j ] = 1 ; else if ( i == 0 ) { if ( check ( 0 , j , x , y )) map [ 0 ][ j ] = 0 ; else map [ 0 ][ j ] = map [ 0 ][ j - 1 ]; } else if ( j == 0 ) { if ( check ( i , 0 , x , y )) map [ i ][ 0 ] = 0 ; else map [ i ][ 0 ] = map [ i - 1 ][ 0 ]; } else { if ( check ( i , j , x , y )) map [ i ][ j ] = 0 ; else map [ i ][ j ] = map [ i - 1 ][ j ] + map [ i ][ j - 1 ]; } } } return map [ n ][ m ]; } int main () { int m , n , x , y ; cin >> m >> n >> x >> y ; long long ans = f ( 0 , 0 , m , n , x , y ); cout << ans << endl ; return 0 ; } OJ提交截图及遇到的问题算法分析与知识点：本题主要采用动态规划的思想来求解，若用递归的方式来求解会导致超时的结果。根据题目分析可得我们令边界都为1，可以写出个状态方程: 有了这个公式就好办了。  递推/ 递归与分治策略-堂练 3-0 ：实验题目：装错信封题目描述：组合学中有这样一个问题：某人给五个朋友写信，邀请他们来家中聚会。请柬和信封交由助手去处理。粗心的助手却把请柬全装错了信封。请问：助手会有多少种装错的可能呢？这个问题是是由当时有名的数学家约翰·伯努利(Johann Bernoulli，1667—1748)的儿子丹尼尔·伯努利(Danid Bernoulli，17OO一1782)提出来的。输入要求：输入数据包含多个多个测试实例，每个测试实例占用一行，每行包含一个正整数n（1<n<=10），n表示朋友的人数。输出要求：对于每行输入请输出可能的错误方式的数量，每个实例的输出占用一行。实验代码及注释: #include <bits/stdc++.h> using namespace std; int f ( int n) { //f函数求装错信封的可能性 if (n == 1 ) //递归边界 return 0 ; else if (n == 2 ) //递归边界 return 1 ; return (n - 1 ) * (f(n - 1 ) + f(n - 2 )); //递归条件 } int main () { int n; while (cin >> n) { int ans = f(n); cout << ans << endl; } return 0 ; } OJ提交截图及遇到的问题：算法分析与知识点：本题主要涉及递归分治的思想先任意指定一封，看它与剩余n -1 封信的组合情况可分为它与第i封交叉犯错和没有与其发生交叉犯错，可列出状态转移方程 3-1 ：实验题目：假币比真币轻题目描述：在n枚外观相同的硬币中，有一枚是假币，并且已知假币与真币的重量不同，已知道假币比真币轻。可以通过一架天平来任意比较两组硬币，设计一个高效的算法来检测这枚假币。要求用分治法称重来实现。输入要求：第1行输入一个整数n（2<=n<=100），表示有n个硬币。第2还开始输入n个整数，表示每个硬币的重量。输出要求：输出一个整数(1..n)，表示假币是第几个硬币。实验代码及注释: #include <bits/stdc++.h> using namespace std; int f ( int coin[], int left, int right) { //f函数求假硬币的位置 if (left == right) //递归边界，返回假硬币的位置 return left; int middle = (left + right) / 2 ; //将硬币分成两堆 int sum1 = 0 , sum2 = 0 ; //记录两堆硬币的总重量 for ( int i = left;i <= middle;i ++ ) { sum1 += coin[i]; } for ( int i = middle + 1 ;i <= right;i ++ ) { sum2 += coin[i]; } if (sum1 / (middle - left + 1 ) > sum2 / (right - middle)) //根据平均重量来判断假硬币在哪一堆 return f(coin, middle + 1 , right); else return f(coin, left, middle); return 0 ; } int main () { int n; int coin[ 101 ]; cin >> n; for ( int i = 0 ;i < n;i ++ ) { cin >> coin[i]; } int ans = f(coin, 0 , n - 1 ); cout << ans + 1 << endl; return 0 ; } OJ提交截图及遇到的问题：算法分析与知识点：本题主要涉及递归分治，将原问题的解分解为若干个子问题，但是这些子问题不需要分别求解，只需求解其中的一个子问题，也无需对子问题进行合并。这样每进行一次分治问题的规模就减小了一半，便于求解。 3-2 ：实验题目：棋盘覆盖题目描述：在一个2^k×2^k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。输入要求：输入一个整数k，k<=5；输入特殊格子的坐标x，y。输出要求：输出一个由数值表示的二维矩阵。填充规则如下：（1）用数值填充方格；（2）特殊方格数值为0；（3）从中心点开始；然后左上、右上、左下、右下的计数顺序填数；同一块用相同数值表示；（4）每个数值占4个位置空间；右对齐，左补空格。实验代码及注释: #include <bits/stdc++.h> using namespace std; int def[ 101 ][ 101 ] = { 0 }; static int t = 0 ; void chess ( int a, int b, int aa, int bb, int length) { //a,b为子棋盘左上角坐标，aa,bb为特殊点坐标，length为子棋盘长度 if (length == 1 ) { return ; } t ++ ; int tem = t; int l = length / 2 ; if (aa < a + l && bb < b + l) { //特殊点在左上的正方形中 chess(a, b, aa, bb, l); } else { def[a + l - 1 ][b + l - 1 ] = tem; //cout<<"左上 "<<l<<" "<<l<<" "<<def[l][l]<<endl; chess(a, b, a + l - 1 , b + l - 1 , l); } if (aa < a + l && bb >= b + l) { //右上角的子棋盘 chess(a, b + l, aa, bb, l); } else { def[a + l - 1 ][b + l] = tem; //cout<<"右上 "<<a+l-1<<" "<<b+l<<" "<<def[a+l][b+l-1]<<endl; chess(a, b + l, a + l - 1 , b + l, l); } if (aa >= a + l && bb < b + l) { //左下角的子棋盘 chess(a + l, b, aa, bb, l); } else { def[a + l][b + l - 1 ] = tem; //cout<<"左下 "<<a+l<<" "<<b+l-1<<" "<<def[a+l-1][b+l]<<endl; chess(a + l, b, a + l, b + l - 1 , l); } if (aa >= a + l && bb >= b + l) { //右下角的子棋盘 chess(a + l, b + l, aa, bb, l); } else { def[a + l][b + l] = tem; //cout<<"右下 "<<a+l<<" "<<b+l<<" "<<def[a+l][b+l]<<endl; chess(a + l, b + l, a + l, b + l, l); } } int main () { int n, a, b, aa, bb, length, m; //a,b是子棋盘左上角的行号和列号 //aa,bb是特殊点的行号和列号 int k, x, y; cin >> k >> x >> y; length = int (pow( 2 , k)); aa = x + 1 ;bb = y + 1 ;a = b = 1 ;m = length; chess(a, b, aa, bb, length); for ( int i = 1 ;i <= m;i ++ ) { //输出结果 for ( int j = 1 ;j <= m;j ++ ) { printf( "%4d" , def[i][j]); if (j == m) { cout << endl; } } } return 0 ; } OJ提交截图及遇到的问题：第一次Compile Error 是因为在计算棋盘一行有多少个格子时使用了pow函数但是没有引入相应的头文件。第二次PE是因为没有注意到题目中每个数字占4个位置的要求。算法分析与知识点：本题主要涉及递归分治的思想，当k>0时，将2^k2^k棋盘分割为4个2^k-12^k-1子棋盘，如图特殊方格必定位于这四个小棋盘中，其余三个子棋盘没有特殊方格，为了将这三个无特殊方格的子棋盘转换为特殊棋盘，我们可以用一个L型骨盘覆盖这三个较小棋盘的会合处，如图所示从图上可以看出，这三个子棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将问题分解为4个较小规模的棋盘覆盖问题。递归地使用这种分割方法，直至棋盘简化为11棋盘，就结束递归。【第二部分/10分】【同类题型实验扩展/可选/会影响分值】题目：正则表达式匹配  给你一个字符串s和一个字符规律p，请你来实现一个支持'.'和''的正则表达式匹配。  '.' 匹配任意单个字符  '' 匹配零个或多个前面的那一个元素  所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。测试数据：结果：实验代码： class Solution { public : bool isMatch(string s, string p) { int m = s.size(); int n = p.size(); auto matches = [ & ]( int i, int j) { if (i == 0 ) { return false ; } if (p[j - 1 ] == '.' ) { return true ; } return s[i - 1 ] == p[j - 1 ]; }; vector < vector < int >> f(m + 1 , vector < int > (n + 1 )); f[ 0 ][ 0 ] = true ; for ( int i = 0 ; i <= m; ++ i) { for ( int j = 1 ; j <= n; ++ j) { if (p[j - 1 ] == '' ) { f[i][j] \|= f[i][j - 2 ]; if (matches(i, j - 1 )) { f[i][j] \|= f[i - 1 ][j]; } } else { if (matches(i, j)) { f[i][j] \|= f[i - 1 ][j - 1 ]; } } } } return f[m][n]; } }; 算法分析与知识点：题目中的匹配是一个「逐步匹配」的过程：我们每次从字符串 p 中取出一个字符或者「字符 + 星号」的组合，并在 s中进行匹配。对于 p 中一个字符而言，它只能在 s中匹配一个字符，匹配的方法具有唯一性；而对于 p 中字符 + 星号的组合而言，它可以在 s 中匹配任意自然数个字符，并不具有唯一性。因此我们可以考虑使用动态规划，对匹配的方案进行枚举。我们用 f[i][j]表示 s的前 i 个字符与 p 中的前 j 个字符是否能够匹配。在进行状态转移时，我们考虑p的第j个字符的匹配情况：也就是说，如果 s 的第 i 个字符与 p 的第 j 个字符不相同，那么无法进行匹配；否则我们可以匹配两个字符串的最后一个字符，完整的匹配结果取决于两个字符串前面的部分。如果 p 的第 j 个字符是 * ，那么就表示我们可以对 p 的第 j − 1 个字符匹配任意自然数次。在匹配次的情况下，我们有

附录

定义大数类，实现大数的算数操作以及输入输出：

class BigInteger { //定义大数类

private :

vector < char > digits;

bool sign; // true for positive, false for negitive

void trim (); // remove zeros in tail, but if the value is 0, keep only one:)

public :

BigInteger( int ); // construct with a int integer

BigInteger(string & );

BigInteger();

BigInteger( const BigInteger & );

BigInteger operator = ( const BigInteger & op2);

BigInteger abs () const ;

BigInteger pow ( int a);

//binary operators

friend BigInteger operator += (BigInteger & , const BigInteger & );

friend BigInteger operator -= (BigInteger & , const BigInteger & );

friend BigInteger operator *= (BigInteger & , const BigInteger & );

friend BigInteger operator /= (BigInteger & , const BigInteger & ) throw (DividedByZeroException);

friend BigInteger operator %= (BigInteger & , const BigInteger & ) throw (DividedByZeroException);

friend BigInteger operator + ( const BigInteger & , const BigInteger & );

friend BigInteger operator - ( const BigInteger & , const BigInteger & );

friend BigInteger operator * ( const BigInteger & , const BigInteger & );

friend BigInteger operator / ( const BigInteger & , const BigInteger & ) throw (DividedByZeroException);

friend BigInteger operator % ( const BigInteger & , const BigInteger & ) throw (DividedByZeroException);

//uniary operators

friend BigInteger operator - ( const BigInteger & ); //negative

friend BigInteger operator ++ (BigInteger & ); //++v

friend BigInteger operator ++ (BigInteger & , int ); //v++

friend BigInteger operator -- (BigInteger & ); //--v

friend BigInteger operator -- (BigInteger & , int ); //v--

friend bool operator > ( const BigInteger & , const BigInteger & );

friend bool operator < ( const BigInteger & , const BigInteger & );

friend bool operator == ( const BigInteger & , const BigInteger & );

friend bool operator != ( const BigInteger & , const BigInteger & );

friend bool operator >= ( const BigInteger & , const BigInteger & );

friend bool operator <= ( const BigInteger & , const BigInteger & );

friend ostream & operator << (ostream & , const BigInteger & ); //print the BigInteger

friend istream & operator >> (istream & , BigInteger & ); // input the BigInteger

public :

static const BigInteger ZERO;

static const BigInteger ONE;

static const BigInteger TEN;

};

const BigInteger BigInteger :: ZERO = BigInteger( 0 );

const BigInteger BigInteger :: ONE = BigInteger( 1 );

const BigInteger BigInteger :: TEN = BigInteger( 10 );

BigInteger :: BigInteger() {

sign = true ;

}

BigInteger :: BigInteger( int val) { // construct with a int integer

if (val >= 0 ) {

sign = true ;

}

else {

sign = false ;

val *= ( -1 );

}

do {

digits.push_back(( char )(val % 10 ));

val /= 10 ;

} while (val != 0 );

}

BigInteger :: BigInteger(string & def) {

sign = true ;

for (string :: reverse_iterator iter = def.rbegin(); iter < def.rend(); iter ++ ) {

char ch = ( * iter);

if (iter == def.rend() - 1 ) {

if (ch == '+' ) {

break ;

}

if (ch == '-' ) {

sign = false ;

break ;

}

digits.push_back(( char )(( * iter) - '0' ));

}

trim();

}

void BigInteger :: trim() {

vector < char >:: reverse_iterator iter = digits.rbegin();

while ( ! digits.empty() && ( * iter) == 0 ) {

digits.pop_back();

iter = digits.rbegin();

}

if (digits.size() == 0 ) {

sign = true ;

digits.push_back( 0 );

}

BigInteger :: BigInteger( const BigInteger & op2) {

sign = op2.sign;

digits = op2.digits;

}

BigInteger BigInteger :: operator = ( const BigInteger & op2) {

digits = op2.digits;

sign = op2.sign;

return ( * this );

}

BigInteger BigInteger :: abs() const {

if (sign) {

return * this ;

}

else {

return - ( * this );

}

BigInteger BigInteger :: pow( int a) {

BigInteger res( 1 );

for ( int i = 0 ; i < a; i ++ ) {

res *= ( * this );

}

return res;

}

//binary operators

BigInteger operator += (BigInteger & op1, const BigInteger & op2) {

if (op1.sign == op2.sign) { //只处理相同的符号的情况，异号的情况给-处理

vector < char >:: iterator iter1;

vector < char >:: const_iterator iter2;

iter1 = op1.digits.begin();

iter2 = op2.digits.begin();

char to_add = 0 ; //进位

while (iter1 != op1.digits.end() && iter2 != op2.digits.end()) {

( * iter1) = ( * iter1) + ( * iter2) + to_add;

to_add = (( * iter1) > 9 ); // 大于9进一位

( * iter1) = ( * iter1) % 10 ;

iter1 ++ ;

iter2 ++ ;

}

while (iter1 != op1.digits.end()) { //

( * iter1) = ( * iter1) + to_add;

to_add = (( * iter1) > 9 );

( * iter1) %= 10 ;

iter1 ++ ;

}

while (iter2 != op2.digits.end()) {

char val = ( * iter2) + to_add;

to_add = (val > 9 );

val %= 10 ;

op1.digits.push_back(val);

iter2 ++ ;

}

if (to_add != 0 ) {

op1.digits.push_back(to_add);

}

return op1;

}

else {

if (op1.sign) {

return op1 -= ( - op2);

}

else {

return op1 = op2 - ( - op1);

}

BigInteger operator -= (BigInteger & op1, const BigInteger & op2) {

if (op1.sign == op2.sign) { //只处理相同的符号的情况，异号的情况给+处理

if (op1.sign) {

if (op1 < op2) { // 2 - 3

return op1 = - (op2 - op1);

}

else {

if ( - op1 > - op2) { // (-3)-(-2) = -(3 - 2)

return op1 = - (( - op1) - ( - op2));

}

else { // (-2)-(-3) = 3 - 2

return op1 = ( - op2) - ( - op1);

}

vector < char >:: iterator iter1;

vector < char >:: const_iterator iter2;

iter1 = op1.digits.begin();

iter2 = op2.digits.begin();

char to_substract = 0 ; //借位

while (iter1 != op1.digits.end() && iter2 != op2.digits.end()) {

( * iter1) = ( * iter1) - ( * iter2) - to_substract;

to_substract = 0 ;

if (( * iter1) < 0 ) {

to_substract = 1 ;

( * iter1) += 10 ;

}

iter1 ++ ;

iter2 ++ ;

}

while (iter1 != op1.digits.end()) {

( * iter1) = ( * iter1) - to_substract;

to_substract = 0 ;

if (( * iter1) < 0 ) {

to_substract = 1 ;

( * iter1) += 10 ;

}

else {

break ;

}

iter1 ++ ;

}

op1.trim();

return op1;

}

else {

if (op1 > BigInteger :: ZERO) {

return op1 += ( - op2);

}

else {

return op1 = - (op2 + ( - op1));

}

BigInteger operator *= (BigInteger & op1, const BigInteger & op2) {

BigInteger result( 0 );

if (op1 == BigInteger :: ZERO || op2 == BigInteger :: ZERO) {

result = BigInteger :: ZERO;

}

else {

vector < char >:: const_iterator iter2 = op2.digits.begin();

while (iter2 != op2.digits.end()) {

if ( * iter2 != 0 ) {

deque < char > temp(op1.digits.begin(), op1.digits.end());

char to_add = 0 ;

deque < char >:: iterator iter1 = temp.begin();

while (iter1 != temp.end()) {

( * iter1) *= ( * iter2);

( * iter1) += to_add;

to_add = ( * iter1) / 10 ;

( * iter1) %= 10 ;

iter1 ++ ;

}

if (to_add != 0 ) {

temp.push_back(to_add);

}

int num_of_zeros = iter2 - op2.digits.begin();

while (num_of_zeros -- ) {

temp.push_front( 0 );

}

BigInteger temp2;

temp2.digits.insert(temp2.digits.end(), temp.begin(), temp.end());

temp2.trim();

result = result + temp2;

}

iter2 ++ ;

}

result.sign = ((op1.sign && op2.sign) || ( ! op1.sign && ! op2.sign));

}

op1 = result;

return op1;

}

BigInteger operator /= (BigInteger & op1, const BigInteger & op2) throw (DividedByZeroException) {

if (op2 == BigInteger :: ZERO) {

throw DividedByZeroException();

}

BigInteger t1 = op1.abs(), t2 = op2.abs();

if (t1 < t2) {

op1 = BigInteger :: ZERO;

return op1;

}

//现在 t1 > t2 > 0

//只需将 t1/t2的结果交给result就可以了

deque < char > temp;

vector < char >:: reverse_iterator iter = t1.digits.rbegin();

BigInteger temp2 ( 0 );

while (iter != t1.digits.rend()) {

temp2 = temp2 * BigInteger :: TEN + BigInteger(( int )( * iter));

char s = 0 ;

while (temp2 >= t2) {

temp2 = temp2 - t2;

s = s + 1 ;

}

temp.push_front(s);

iter ++ ;

}

op1.digits.clear();

op1.digits.insert(op1.digits.end(), temp.begin(), temp.end());

op1.trim();

op1.sign = ((op1.sign && op2.sign) || ( ! op1.sign && ! op2.sign));

return op1;

}

BigInteger operator %= (BigInteger & op1, const BigInteger & op2) throw (DividedByZeroException) {

return op1 -= ((op1 / op2) * op2);

}

BigInteger operator + ( const BigInteger & op1, const BigInteger & op2) {

BigInteger temp(op1);

temp += op2;

return temp;

}

BigInteger operator - ( const BigInteger & op1, const BigInteger & op2) {

BigInteger temp(op1);

temp -= op2;

return temp;

}

BigInteger operator * ( const BigInteger & op1, const BigInteger & op2) {

BigInteger temp(op1);

temp *= op2;

return temp;

}

BigInteger operator / ( const BigInteger & op1, const BigInteger & op2) throw (DividedByZeroException) {

BigInteger temp(op1);

temp /= op2;

return temp;

}

BigInteger operator % ( const BigInteger & op1, const BigInteger & op2) throw (DividedByZeroException) {

BigInteger temp(op1);

temp %= op2;

return temp;

}

//uniary operators

BigInteger operator - ( const BigInteger & op) { //negative

BigInteger temp = BigInteger(op);

temp.sign = ! temp.sign;

return temp;

}

BigInteger operator ++ (BigInteger & op) { //++v

op += BigInteger :: ONE;

return op;

}

BigInteger operator ++ (BigInteger & op, int x) { //v++

BigInteger temp(op);

++ op;

return temp;

}

BigInteger operator -- (BigInteger & op) { //--v

op -= BigInteger :: ONE;

return op;

}

BigInteger operator -- (BigInteger & op, int x) { //v--

BigInteger temp(op);

-- op;

return temp;

}

bool operator < ( const BigInteger & op1, const BigInteger & op2) {

if (op1.sign != op2.sign) {

return ! op1.sign;

}

else {

if (op1.digits.size() != op2.digits.size())

return (op1.sign && op1.digits.size() < op2.digits.size())

|| ( ! op1.sign && op1.digits.size() > op2.digits.size());

vector < char >:: const_reverse_iterator iter1, iter2;

iter1 = op1.digits.rbegin();

iter2 = op2.digits.rbegin();

while (iter1 != op1.digits.rend()) {

if (op1.sign && * iter1 < * iter2) {

return true ;

}

if (op1.sign && * iter1 > * iter2) {

return false ;

}

if ( ! op1.sign && * iter1 > * iter2) {

return true ;

}

if ( ! op1.sign && * iter1 < * iter2) {

return false ;

}

iter1 ++ ;

iter2 ++ ;

}

return false ;

}

bool operator == ( const BigInteger & op1, const BigInteger & op2) {

if (op1.sign != op2.sign || op1.digits.size() != op2.digits.size()) {

return false ;

}

vector < char >:: const_iterator iter1, iter2;

iter1 = op1.digits.begin();

iter2 = op2.digits.begin();

while (iter1 != op1.digits.end()) {

if ( * iter1 != * iter2) {

return false ;

}

iter1 ++ ;

iter2 ++ ;

}

return true ;

}

bool operator != ( const BigInteger & op1, const BigInteger & op2) {

return ! (op1 == op2);

}

bool operator >= ( const BigInteger & op1, const BigInteger & op2) {

return (op1 > op2) || (op1 == op2);

}

bool operator <= ( const BigInteger & op1, const BigInteger & op2) {

return (op1 < op2) || (op1 == op2);

}

bool operator > ( const BigInteger & op1, const BigInteger & op2) {

return ! (op1 <= op2);

}

ostream & operator << (ostream & stream, const BigInteger & val) { //print the BigInteger

if ( ! val.sign) {

stream << "-" ;

}

for (vector < char >:: const_reverse_iterator iter = val.digits.rbegin(); iter != val.digits.rend(); iter ++ ) {

stream << ( char )(( * iter) + '0' );

}

return stream;

}

istream & operator >> (istream & stream, BigInteger & val) { //Input the BigInteger

string str;

stream >> str;

val = BigInteger(str);

return stream;

}

本文章由word文档转换而成