MATLAB 主成分分析

回到主页

主成分分析基本原理

  • 当我们拿到一组数据，例如中学生身高、胸围、体重这三组数据，我们可以拿这三组数据来描述一个中学生的身形。但是很多情况下，这样的数据种类太多而且过于杂乱，无法很好地描述实体。

  • 主成分分析的思想就是，在给出数据 \(X_1、X_2、X_3\quad ... \quad X_n\) 基础上，创造新的一组数据 \(Y_1、Y_2、Y_3\quad ... \quad Y_n\) 这组新的数据能更好地描述实体。

  • Y能更好地描述，主要是因为 Y 中含有更多的信息，通常来说，越靠前的 Y 包含有效信息越多，我们用贡献率描述包含成分的多少。所有 Y 的贡献率为1，一般来说，前一到两个Y就能描述 85% 以上信息。

  • Y 是由 X 线性表示出来的，也就是说，从原来每个成分里面按比例线性相加，形成更加能描述实体的值。

MATLAB函数介绍

X1 = zscore(X)

将数据标准化，原始数据由于单位等的不同，会有数值过大和过小的情况，需要将数据进行标准化，然后对标准化的数据进行分析。

[coeff, score, latent] = pca(X)

  • 对矩阵X进行主成分分析。

  • X 每一列是一个指标 \(X_n\)，每一行是一个样本。

  • coeff 给出主成分变换矩阵，每一列的系数代表这个主成分含有原函数$X$的系数，即第一列是 \(Y_1\) 第二列是 \(Y_2\)；第一行是 \(X_1\) 系数，第二行是 \(X_2\) 系数。

  • score 是得分，即每个主成分每个样本的得分情况，即描述每个样本 \(Y\) 的数据。

  • latent 是每个主成分 \(Y\) 的特征值，每个特征值占总特征值和的比重就是贡献率，贡献率即代表了对事物的描述程度。

sum 和 cumsum

  • sum 用于求和，cumsum用于求阶梯和，对 latent 使用，来计算累积贡献率。

[B,I] = sort(A,direction)

  • 对矩阵 A 进行排序，每一行为一个整体，以第一列元素大小为依据，direction 可以选择 ascend 或 descend

  • 返回的 B 为新矩阵，I 为之前矩阵的行序号，注意 I 是一个矩阵，只不过每行元素相同。

主成分分析步骤

  • 进行标准化处理

  • 进行主成分分析

  • 根据结果，选择主成分，写出表达式

  • 根据数据进一步分析

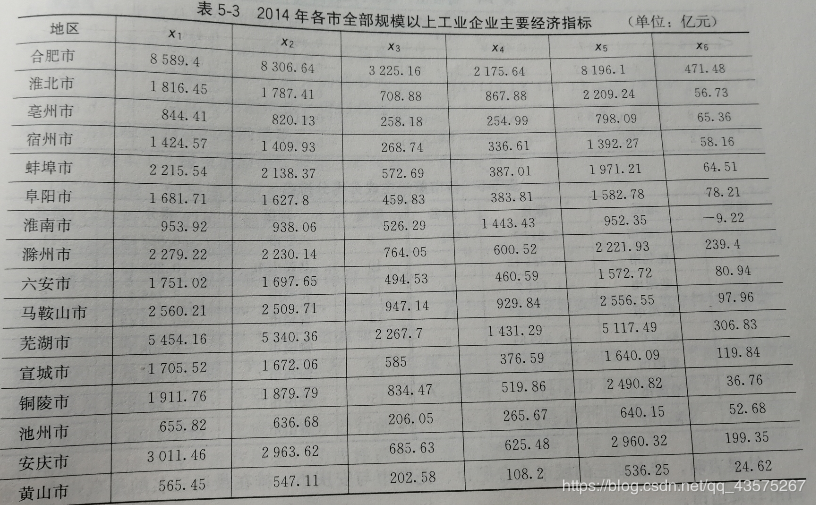
应用——综合评价

在这里插入图片描述

A=[8589.4	8306.64	3225.16	2175.64	8196.1	471.48
1816.45	1787.41	708.88	867.88	2209.24	56.73
844.41	820.13	258.18	254.99	798.09	65.36
1424.57	1409.93	268.74	336.61	1392.27	58.16
2215.54	2138.37	572.69	387.01	1971.21	64.51
1681.71	1627.8	459.83	383.81	1582.78	78.21
953.92	938.06	526.29	1443.43	952.35	-9.22
2279.22	2230.14	764.05	600.52	2221.93	239.4
1751.02	1697.65	494.53	460.59	1572.72	80.94
2560.21	2509.71	947.14	929.84	2556.55	97.96
5454.16	5340.36	2267.7	1431.29	5117.49	306.83
1705.52	1672.06	585	376.59	1640.09	119.84
1911.76	1879.79	834.47	519.86	2490.82	36.76
655.82	636.68	206.05	265.67	640.15	52.68
3011.46	2963.62	685.63	625.48	2960.32	199.35
565.45	547.11	202.58	108.2	536.25	24.62];
A = zscore(A);
[coeff, score, latent] = pca(A);
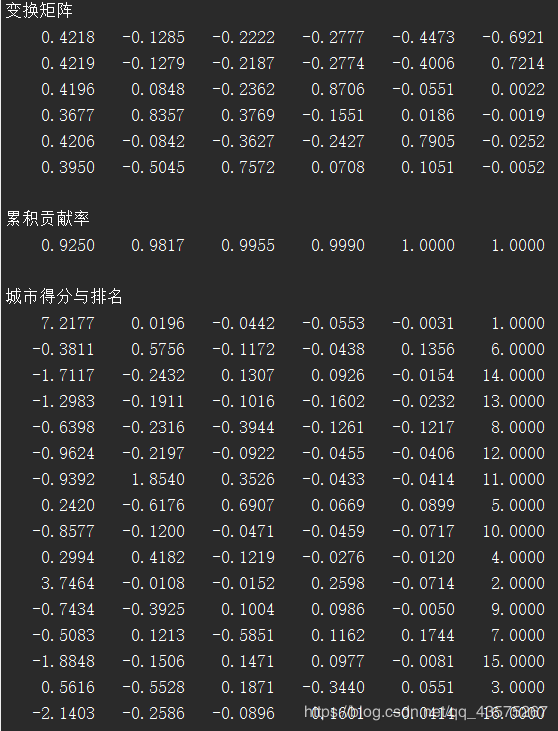
fprintf('变换矩阵\n')
disp(coeff);
latent_sum = sum(latent);
latent = cumsum(latent/latent_sum);
fprintf('累积贡献率\n')
disp(latent');
[range_score,I] = sort(score,'descend');
rangeIndex = size(score,2);  %最后一行插入排名
for i = 1:size(I,1)
    score(I(i,1),rangeIndex) = i;
end
fprintf('城市得分与排名\n');
disp(score)

在这里插入图片描述

所以我们选取$Y_1、Y_2$ 就可以描述 98.17% 的数据，根据第一个主成分得分进行排名。其中：

\[ Y_1=0.4218X_1+0.4219X_2+0.4196X_3+0.3677X_4+0.4206X_5+0.3950X_6 \]

\[ Y_2=-0.1285X_1-0.1279X_2+0.0848X_3+0.8357X_4-0.0842X_5-0.5045X_6 \]

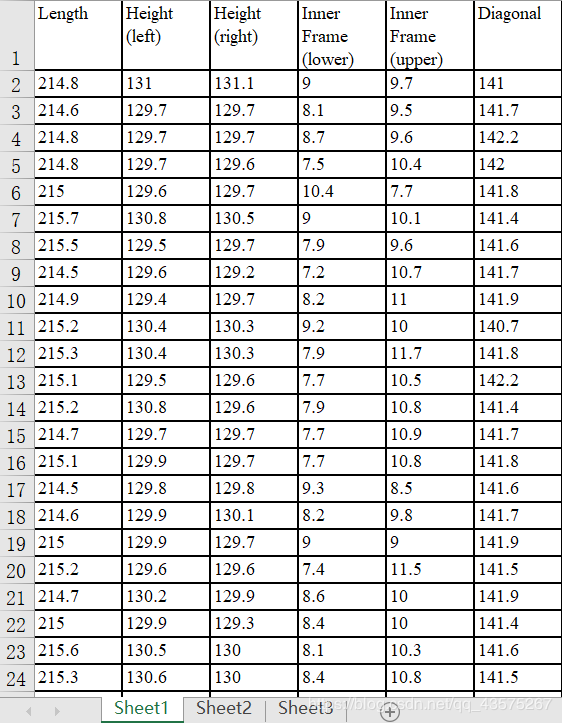
应用——分类

现在有一些货币的数据，前100组是真钱，后100组是假钱。

在这里插入图片描述

%已导入数据cX
X = zscore(X);
[coeff, score, latent] = pca(X);
latents = sum(latent);
latent = cumsum(latent/latents);
fprintf('贡献率');
disp(latent');
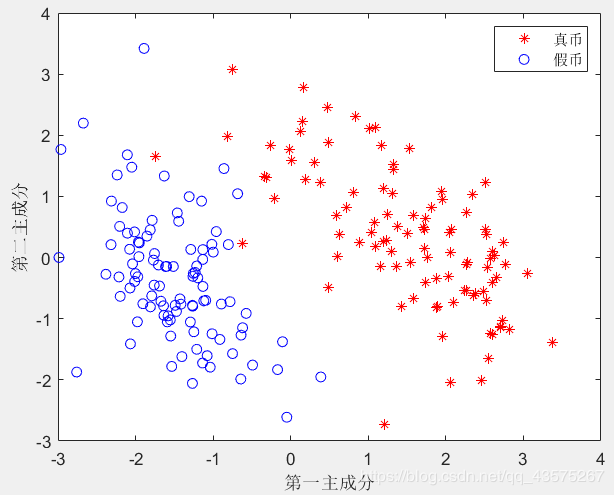
plot(score(1:100,1),score(1:100,2),'r*',...
    score(101:200,1),score(101:200,2),'bo');
xlabel('第一主成分'); ylabel('第二主成分');
legend('真币','假币');

在这里插入图片描述

在这里插入图片描述

如图，已经基本可以确定假币和真币，但是由于前两个贡献值不够，所以图像还有些许问题。

根据协方差矩阵计算特征值

  • 先计算数据的协方差矩阵，将矩阵用 eig 函数分解，即 [v,d] = eig(cov(X))；

  • 主成分贡献率为 q = sum(d)/sum(sum(d))

  • 主成分得分为 X * v；加权主成分得分为 X .* (ones(size(X,1),1) * q) * v

[M,N] = size(X);
[v,d] = eig(cov(X));
q = sum(d)/sum(sum(d));
w = q/sum(q);
F = X.*(ones(M,1)*w)*v;
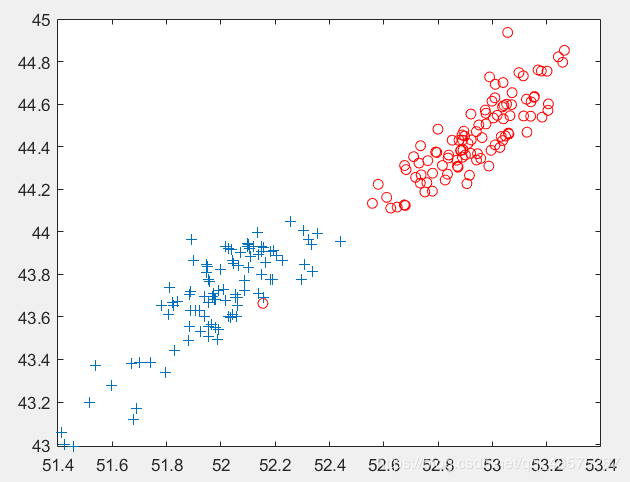
plot(F(1:100,6),F(1:100,5),'or',F(101:200,6),F(101:200,5),'+')

在这里插入图片描述

如图所示，区分更加明显

本文章使用limfx的vsocde插件快速发布