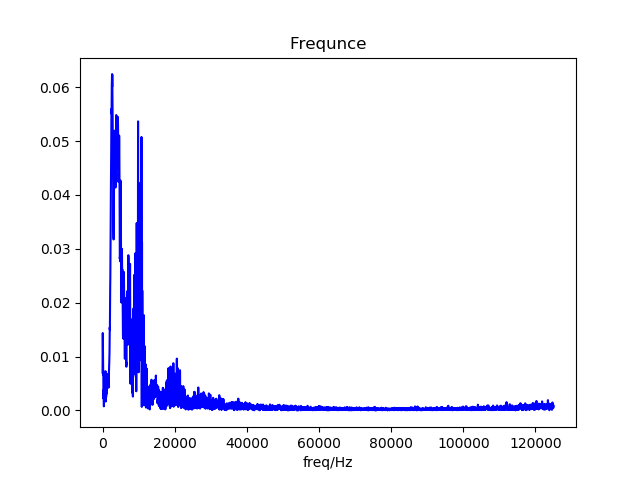
对米尔诺夫信号时间切片进行傅里叶分析
1.scipy.fftpack.fft
y = scipy.fftpack.fft(x)
输入:N个采样点数据,len(x)=N。
输出:N个点的以复数形式记录的FFT结果,len(y)=N。
fft返回的是一个复数数组,每个数字表示为一个正弦波。通常一个波形由振幅、相位、频率、三个变量确定,可从fft返回复数数组里获取。
振幅:abs_y = np.abs(y)
相位:angle_y = np.angle(y)
频率:freq = [i*Fs/(N-1) for i in range(N)]
其中,N为采样点个数;Fs为采样频率(如:ip:10kHz;MA_POL_CA01T :250kHz)
因为,y[1:N/2]包含正频率项,y[N/2 : ]包含负频率项。正频率项就是转化后的频域信号,通常我们只需要正频率项,及前面N/2项,负频率项是计算的中间结果。如果直接 plt.plot(freq,abs_y) ,如下图,会出现对称的信号频率,但右侧的频率没有实际意义。 
plt.plot(freq[:int(N/2)],abs_y[:int(N/2)])
注意一点:这里的幅值不是实际幅值。要得到实际幅值:0Hz处,即abs_y[0]需除以N;其他谐波处,即abs_y[1:]需除以N/2。
2.对米尔诺夫信号时间窗切片进行傅里叶分析
破裂预测中,我们以32ms为一个时间窗切片。现在对MA_POL_CA01T信号切片进行傅里叶分析。MA_POL_CA01T的采样频率是250kHz,不对信号降采样。
则:N = 32*250 = 8000 ; Fs = 250000
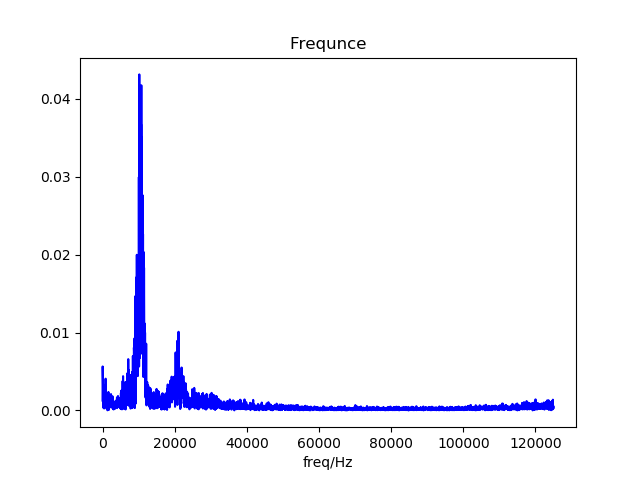
将一炮进行时间窗切片,以时间顺序依次画出每1ms对应的切片的傅里叶频率幅值图(实际幅值)。 从0.2s到下降时刻。 对于正常炮,各时刻频率幅值图大体上是不变的。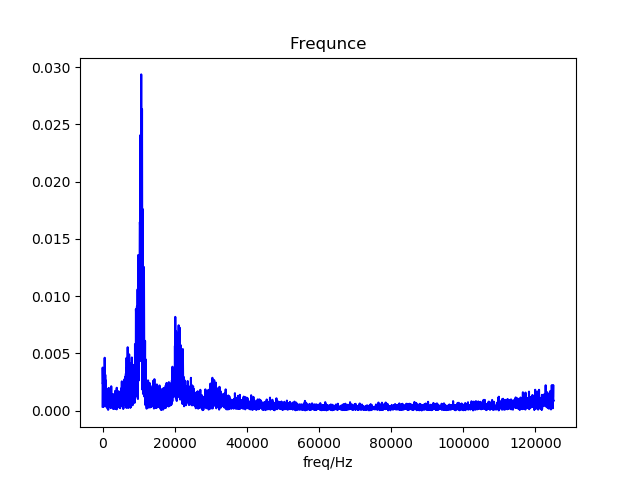
本文章使用limfx的vsocde插件快速发布