图算法——最短路径
注:本文属于整理的个人笔记,参考文献已给出链接
一、图基础
基本概念:
-
稀疏图:边数m远小于顶点数n的平方的图(m<)
稠密图:边数m接近顶点数n的平方的图
更具体地说,满足 |m|<|n|log2|n| 的时候,可以将图G定义为稀疏图,反之则为稠密图
-
邻接矩阵(适用于稠密图):使用用二维矩阵存图
邻接表(适用于稀疏图,避免空间浪费):使用链表、vector数组等方式存图
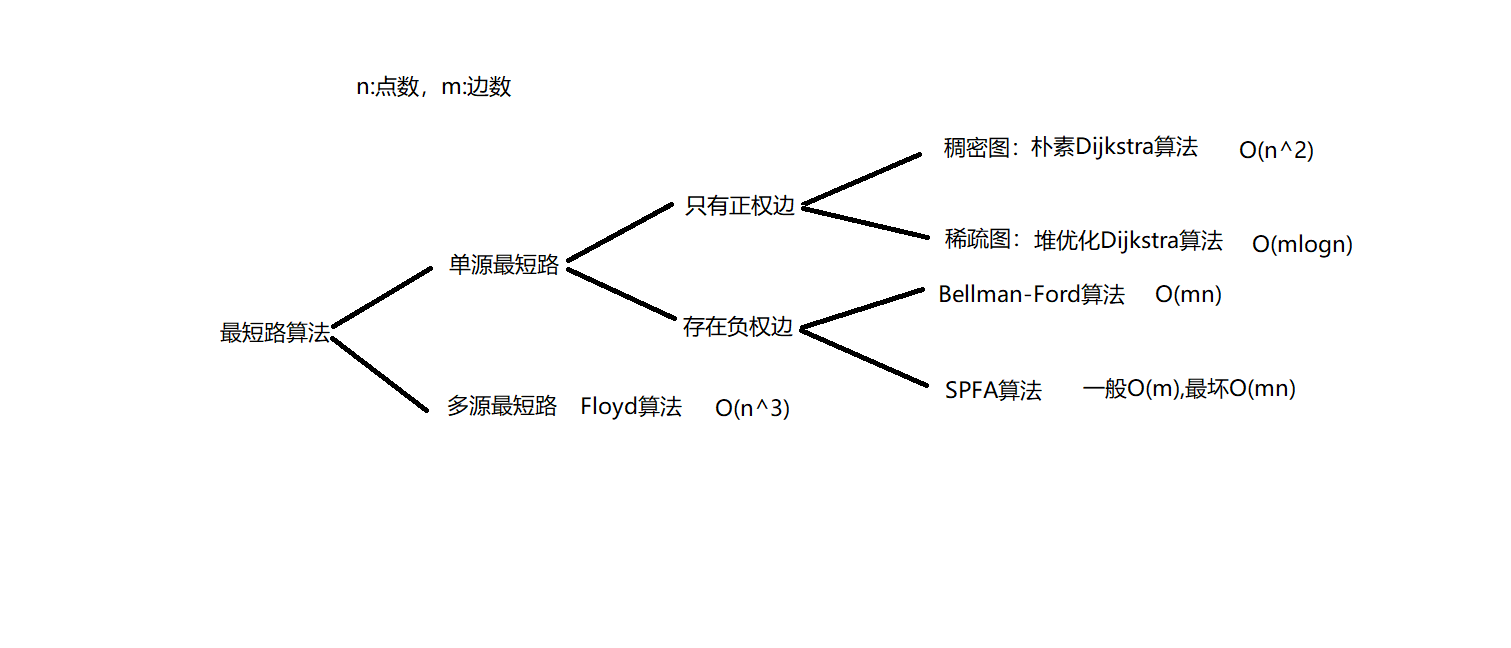
二、最短路径算法
参考:Kaptree视频讲解、麦克老师讲算法 、Algorithm、AcWing算法课程等
注:所有算法只讲思路不作证明
松弛操作:对于一个边(u,v),松弛操作对应下面的式子:dis[v]=min(dis[v],dis[u]+w(u,v))。开始可能源点S 到v的路径为S−>v,如果说经过u点再到v的权值比直接到v小那么我们就更新一下路径最小值,将源点到v点的距离更新的一个操作就是松弛操作
Dijkstra算法
注:n:顶点数,m:边数,start:源点(路径中的起始节点)
-
核心思想:贪心算法
-
思路:将结点分成两个集合:已确定最短路长度的点集(记为S集合)的和未确定最短路长度的点集(记为T集合),一开始所有的点都属于T集合(定义一个bool类型的数组用以区分两个集合)。
-
int dis[n] (dis数组表示源点到该点的最短距离,初始化dis[start]=0,其余节点的 dis值为无穷大)
bool vis[n] (初始化所有节点为false)
-
从T集合中选取一个从源点到该点的最短路值最小的点x,然后放入S集合中(vis[x]=true)
-
遍历 x的所有出边 (x,y,z) (//x点到y点的距离是z//), 若 dis[y]>dis[x]+z, 则令 dis[y]=dis[x]+z(松弛操作)
-
重复 2,3 两步,直到所有点都加入集合S
-
我们发现,对于寻找dis值最小的点的操作,我们通过不同的方式维护的话那么算法的整体复杂度就会不同
(1) 朴素Dijkstra算法:不使用任何数据结构进行维护,每次 2 操作执行完毕后,直接在T集合中暴力寻找最短路长度最小的结点。3操作总时间复杂度为O(m),2操作总时间复杂度为O(),全过程的时间复杂度为O(+m)=O()
(2) 堆优化Dijkstra算法:
二叉堆:每成功松弛一条边(u,v),就将v插入二叉堆中(如果v已经在二叉堆中,直接修改相应元素的权值即可),2操作直接取堆顶结点即可。共计O(m)次二叉堆上的插入(修改)操作,O(n)次删除堆顶操作,而插入(修改)和删除的时间复杂度均为O(logn),时间复杂度为O((n+m)×logn)=O(mlogm)
优先队列:和二叉堆类似,但使用优先队列时,如果同一个点的最短路被更新多次,因为先前更新时插入的元素不能被删除,也不能被修改,只能留在优先队列中,故优先队列内的元素个数是O(m)的,时间复杂度为O(mlogm)
Fibonacci 堆:和前面二者类似,但 Fibonacci 堆插入的时间复杂度为O(1),故时间复杂度为O(nlogn+m)=O(nlogn),时间复杂度最优。但因为Fibonacci 堆较二叉堆不易实现,效率优势也不够大 ,算法竞赛中较少使用。
故稠密图中使用朴素Dijkstra算法,稀疏图中使用堆优化Dijkstra算法
- 代码实现
模板题:https://ac.nowcoder.com/acm/contest/27274/E
朴素Dijkstra(稠密图)
#include<cstdio>
#include<algorithm>
#include<vector>
#include<iostream>
#include<cstring>
using namespace std;
#define INF 0x3f3f3f3f
const int N = 1e3+10;
int f[N][N],n,m,dis[N];
bool vis[N];
void DJ(int s){
for(int i = 1;i <= n; ++i) dis[i] = INF,vis[i] = false;
dis[s] = 0; //初始化dis,vis数组
for(int i = 1;i <= n; ++i) {
int t = -1;
for(int j = 1;j <= n; ++j) {
if(!vis[j] && (t == -1 || dis[j] < dis[t])) t = j;
}//寻找dis最小值
if(t == -1) return;
vis[t] = true;
for(int j = 1;j <= n; ++j){
if(dis[j] > dis[t] + f[t][j])
dis[j] = dis[t] + f[t][j];
}
}
}
int main()
{
int s,t;
cin>>n>>m>>s>>t;
int u,v,w;
memset(f,0x3f,sizeof f);//memset函数初始化f数组所有值为无穷大,与用for循环遍历进行初始化同理
for(int i = 1;i <= m; ++i){
cin>>u>>v>>w;
f[v][u] = min(f[v][u],w);
f[u][v] = min(f[u][v],w);//重边取最小值
}
DJ(s);
if(dis[t] == INF) cout<<"-1"<<endl;//最短路不存在
else cout<<dis[t]<<endl;
return 0;
}
堆优化Dijkstra(稀疏图)
#include<cstdio>
#include<algorithm>
#include<vector>
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3f
const int N = 2e6+10;
int dis[N],n,m;
bool vis[N];
vector<PII> E[N];
void DJ(int s){
for(int i = 1;i <= n; ++i) dis[i] = INF,vis[i] = false;
priority_queue<PII,vector<PII>,greater<PII> > que; //小根堆,根据dis值进行排序
que.push({0,s});//源点放入堆中,源点dis值为0
dis[s] = 0;
while(!que.empty()){
int t = que.top().second;
que.pop();
if(vis[t]) continue;// 重边的话不用更新其他点了
vis[t] = true;//标记 t 已经确定最短路
for(int i = 0,l = E[t].size();i < l; ++i) {
int j = E[t][i].first,w = E[t][i].second;
if(dis[j] > dis[t] + w){
dis[j] = dis[t] + w;
que.push({dis[j],j});//放入堆中
}
}
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//加快cin,cout的读取速度,数据范围大于1e5时建议使用scanf和printf读取数据
int s,t;
cin>>n>>m>>s>>t;
int u,v,w;
for(int i = 1;i <= m; ++i){
cin>>u>>v>>w;
E[u].push_back({v,w});
E[v].push_back({u,w});
}
DJ(s);
if(dis[t] == INF) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
return 0;
}
Bellman-Ford 算法
- 思路
Bellman算法要做的事就是对于图中所有的边,我们都进行一次松弛操作,那么完成这整个操作的复杂度大概在O(M) ,然后一直循环进行这个操作,直到不能进行松弛操作为止,就说明单源最短路已经全部求完,那么我们需要多少次这样的完整操作呢?在最短路存在的情况下,由于一次松弛操作会使最短路的边数至少+1 ,而最短路的边数最多为N−1 ,因此整个算法最多执行N−1轮松弛操作。故总时间复杂度为O(NM)
- 负环问题
上面提到了我们在求最短路存在的情况最多执行N−1轮松弛操作,如果数据中出现了负环,那么我们在第N轮操作的时候也会更新,故可以用此算法判断图中是否存在负环
注意一点 :以S点为源点跑 Bellman-Ford 算法时,如果没有给出存在负环的结果,只能说明从S点出发不能抵达一个负环,而不能说明图上不存在负环。 因为这个图可能是不连通的 ,那么对于不连通的图我们应该建一个虚点或者称之为 超级源点 ,让这个点连向每一个其他的点并且权值为0,然后再来跑Bellman-Ford 算法
- 代码实现
模板题:https://ac.nowcoder.com/acm/contest/27274/E
Bellman-Ford 算法:
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
#include<vector>
const int INF = 0x3f3f3f3f;
const int N = 10000+10;
using namespace std;
struct Node{
int u,v,w;
};
vector<Node> E;
int n,m,s,t;
int dis[N];
void bellman_ford(int s){
for(int i = 1;i <= n; ++i) dis[i] = INF;
dis[s] = 0;
//Bellman-Ford 算法第一层for循环的实际意义
//经过 n - 1次松驰
//对所有边进行一次松弛操作,就求出了源点到所有点经过的边数最多为1的最短路
//对所有边进行两次松弛操作,就求出了源点到所有点经过的边数最多为2的最短路
//....
//对所有边进行n- 1次松弛操作,就求出了源点到所有点经过的边数最多为n - 1的最短路
//Bellman-Ford 算法第二层for循环枚举边的个数,而不是点的个数,注意无向图边的个数,一来一回当成两条边
for(int i = 1;i <= n; ++i)//实际上i到n-1就行{
int check=0;
for(int j = 0;j < 2 * m; ++j) {
int u = E[j].u,v = E[j].v,w = E[j].w;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
check=1;
}
}
if(check==0)break;//循环过程中未进行松弛操作,说明所有点已经确定最短路径,提前结束循环
}
}
int main()
{
cin>>n>>m>>s>>t;
int u,v,w;
for(int i = 1;i <= m; ++i) {
cin>>u>>v>>w;
E.push_back({u,v,w});
E.push_back({v,u,w});
}
bellman_ford(s);
if(dis[t] >= INF / 2) //此处判断条件不能写dis[t]==INF,因为因为Bellman-Ford 算法要遍历每条边,而其实要更新的只是之前更新过的结点的邻节点(没更新过的边相当于根本不关联,遍历根本没有意义) 同时,因为负边的存在,Bellman-Ford 算法会进行毫无意义的更新(从INF到INF减去负权边),所以最后判定是否有最短路径不能用dis[N]==INF,而是要dis[N]>INF/2,而对于SPFA算法,只更新邻节点,也就意味着只会更新联通的点,就不会存在无意义的更新,因此最后只需要dis[N]==INF即可
cout<<"-1"<<endl;
else
cout<<dis[t]<<endl;
}
判断负环:如果发现第N轮操作也更新了那么说明存在负权回路
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#define INF 0x3f3f3f3f
const int N = 2e6+10;
int n,m,q,k;
struct Edge{
int u,v,w;
}E[N];
int dis[N];
bool bellman_ford(){
for(int i = 1;i <= n; ++i)
for(int j = 0;j < m; ++j) {
int u = E[j].u,v = E[j].v,w=E[j].w;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
if(i == n)
return true;
}
}
return false;
}
int main()
{
cin>>n>>m;
for(int i = 0;i < m; ++i) {
int u,v,w;
cin>>u>>v>>w;
E[i]={u,v,w};
}
bool k = bellman_ford();
if(k) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
return 0;
}
SPFA算法
-
思路
其实SPFA算法就是Bellman-Ford 算法加上了队列优化 ,从上面的Bellman-Ford 算法能知道我们将每一个边都松弛了N−1次,实际上我们没必要松弛每一个点,因为有些点实际上是不用松弛太多或者说不用松弛的,那么我们希望去掉一些无用的松弛操作,这个时候我们用队列来维护哪些点可能会需要松弛操作,这样就能只访问必要的边了。
用dis数组记录源点到有向图上任意一点距离,其中源点到自身距离为0,到其他点距离为INF。将源点入队,并重复以下步骤:
- 队首t出队,并将t标记为没有访问过,方便下次入队松弛
- 遍历所有以队首为起点的有向边(t,j),若dis[j]>dis[t]+w(t,j),则更新dis[j]
- 如果点j不在队列中,则j入队,并将j标记为访问过
- 若队列为空 ,跳出循环;否则执行第一步
SPFA在形式上和广度优先搜索非常类似,不同的是广度优先搜索中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是说一个点修改过其它的点之后,过了一段时间可能会获得更短的路径,于是再次用来修改其它的点,这样反复进行下去。 算法时间复杂度:O(KM),M是边数。K是常数,平均值为2,但是实际上SPFA的算法复杂度是 O(NM) ,可以构造出卡SPFA的数据,让SPFA超时。
- 代码实现
SPFA最短路代码实现
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
const int INF = 0x3f3f3f3f;
const int N = 10000+10;
using namespace std;
struct Node{
int v,w;
};
vector<Node> E[N];
int n,m,s,t;
int dis[N];
bool vis[N];
void SPFA(int s){
for(int i = 1;i <= n; ++i)
vis[i] = false,dis[i] = INF;
queue<int> que;
que.push(s);
dis[s] = 0,vis[s] = true;
while(!que.empty()){
int t = que.front();
que.pop();
vis[t] = false;//可能重新入队
for(int i = 0,l = E[t].size();i < l; ++i) {
int j = E[t][i].v;
int k = E[t][i].w;
if(dis[j] > dis[t] + k){
dis[j] = dis[t] + k;
if(!vis[j]){
vis[j] = true;
que.push(j);
}
}
}
}
}
int main()
{
cin>>n>>m>>s>>t;
int u,v,w;
for(int i = 1;i <= m; ++i) {
cin>>u>>v>>w;
E[u].push_back({v,w});
E[v].push_back({u,w});
}
SPFA(s);
if(dis[t] >= INF / 2) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
}
SPFA判负环实现
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<queue>
#include<vector>
using namespace std;
#define PII pair<int,int>
const int N = 2e6+10;
int n,m,q;
vector<PII> E[N];
int dis[N],cnt[N];//cnt[x]表示从源点到x点所经过的边数
bool vis[N];
void spfa(){
queue<int> que;
for(int i = 1;i <= n; ++i) que.push(i),vis[i] = true;
while(!que.empty()){
int t = que.front();
que.pop();
vis[t] = false;//表明t这个点已经离开这个队列了
for(int i = 0,l = E[t].size();i < l; ++i) {
int j = E[t][i].first,k = E[t][i].second;
if(dis[j] > dis[t] + k) {
dis[j] = dis[t] + k;
cnt[j] = cnt[t] + 1;//从源点到j点所经过的边数等于从源点到t点所经过的边数加上从t到j这一条边
if(cnt[j] >= n) {//找到负权边
cout<<"Yes"<<endl;
return;
}
if(!vis[j])//将j这个点重新加入队列
que.push(j),vis[j] = true;
}
}
}
cout<<"No"<<endl;
}
int main()
{
cin>>n>>m;
int u,v,w;
for(int i = 0;i < m; ++i) {
cin>>u>>v>>w;
E[u].push_back({v,w});
}
spfa();
return 0;
}
- SPFA判断正环
关于SPFA判断正环的可以参考这一题:https://blog.csdn.net/m0_46201544/article/details/123011318
Floyd算法
-
思想:动态规划
-
原理:我们定义一个三维数组f[k][u][v]表示的是允许经过[1,k]中的点从u到v的最小距离,换句话说从1到k这些点可以作为u到v的中间节点,当然没也可以不经过,很显然我们如果要求解u到v的最小距离那么就是f[n][u][v](假设当前的图中有n个点的话),那么我们考虑怎么来维护这个关系呢,首先初始化来说,f[0][u][v]先初始化为INF,如果有边连接的话,那么我们取一个min就好,还有就是如果u和v相等的话应该初始化为0,那么我们就能推出这个状态是如何转移的:
f[k][u][v]=min(f[k−1][u][v],f[k−1][u][k]+f[k−1][k][v])
我们发现我们这个第一维的k其实最多能用到当前这一层以及上一层的状态,那么我们可以通过 滚动数组 优化将其去掉,即定义一个二维数组f[u][v],状态转移方程:
f[u][v]=min(f[u][v],f[u][k]+f[k][v])
- 代码实现:
void Floyd(){
for(int k = 1;k <= n; ++k)
for(int i = 1;i <= n; ++i)
for(int j = 1;j <= n; ++j)
f[i][j] = min(f[i][j],f[i][k]+f[k][j]);
}
算法适用分析
多源最短路经:Floyd算法
单源最短路径: 正权图:稠密图中使用朴素Dijkstra算法,稀疏图中使用堆优化Dijkstra算法
存在负权值:(SPFA算法是队列优化的 Bellman-Ford 算法,后者能做的前者基本都能做,如判断负权图,而且速度更快)一般用SPFA算法,但处理有边数限制的最短路时用Bellman-Ford 算法,不能用SPFA算法
其他补充
- 路径打印问题
我们可以定义一个pre数组,然后pre[i]记录的是上一个位置是哪一个节点,当然初始的时候我们全部初始化为−1,然后每次松弛操作的时候就更新一下上一个节点的位置,最后打印的时候要么递归打印,那么手动写栈打印,这个方法不只是适用于Dijkstra,而且也适用于其他最短路算法,如SPFA、Bellman_ford、Floyd等等
那么简单描述一下打印函数
void print(int t){
for(int i = t;~i;i=pre[i]){
cout<<i;
if(i != s) cout<<" -> ";
}
}
- 路径统计问题
其实我们在 松弛操作 的时候就能记录or更新从源点到当前点的路径条数,模板题:最短路计数
本文章使用limfx的vscode插件快速发布