数学建模论文学习笔记

回到主页

来自MCM_C_2318982

  1. 可以通过皮尔逊系数来探讨变量与因变量之间的关系。
  2. LASSO可以用于过滤多余变量。
    接下来介绍一下LASSO回归是什么。
    1. 我们首先介绍一下正则化。
      正则化是为了防止过拟合而引入的一个概念。而正则化项则是基于正则化而衍生出的一个式子。它的作用就是提高模型的稳定性。实现方式是通过增加一个惩罚项，使得有限的权重集中到更重要的维度上。
    2. 接下来介绍LASSO回归。首先是LASSO回归的表达式：
L_{LASSO} = \sum_{i = 1}^{N}(y_i - \hat{y_i})^2+\lambda ||\mathbf{W} ||_1

|| \mathbf{W}||_1 = \sum_{i = 1}^D|w_i|
  1. LASSO回归后，不重要的系数可以为0，由此可以用来减少多余的变量，防止过拟合发生。
  2. 求解办法：坐标下降法：
    1. 依次对进行寻优，使趋向于0
    2. 寻优过程中只对进行修改，其他不变。
    3. 迭代，知道每个都不产生显著性变化为之。
    4. 下降梯度搜索法：
  3. 回归前提：误差服从独立同分布和正态分布。
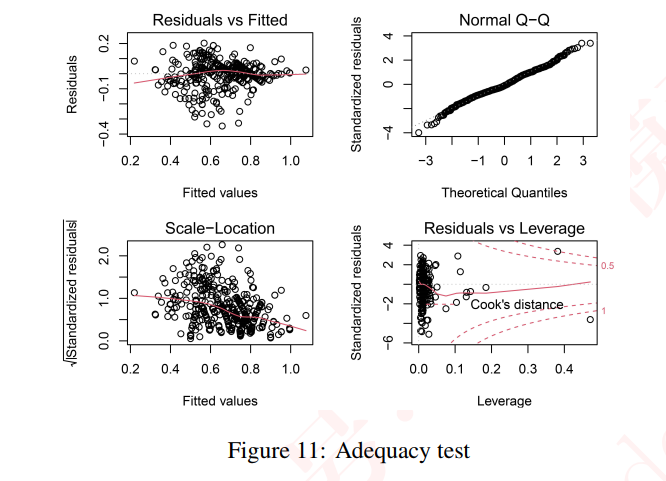
  4. 如图
    1. 右上角为残差正态性检验，若都在直线周围，则不能怀疑正态性假设。
    2. 左下角是残差独立同方差检验图，若没有显著趋势则可认为误差是独立同分布。
    3. 左上角是模型线性侧视图，没有明显曲线关系，因此线性被认为是有效的。 Alt text
  5. 检验多重共线性的一种方法是计算方差膨胀因子（V IF），如果单个变量的方差膨胀因子大于10，则认为存在多重共线性。计算模型（x）的两个变量的V IF的结果如表4所示，这表明模型中不存在显著的多重共线性。
  6. 高斯过程：
    1. 一元高斯分布：
p(x) = \frac{1}{\sigma \sqrt{2\pi }} e^{-\frac{(x-\mu)^2}{2\sigma^2}}

这是我们熟悉的钟形曲线，正态分布，均值和方差决定了曲线的形状。

  1. 现在上升到多元：
p(x_1, x_2, \ldots, x_n) = \prod_{i = 1}^np(x_i)= \frac{e^{-\frac{1}{2} [ \frac{(x_1-\mu_1)^2}{\sigma_1^2}+\frac{(x_2-\mu_2)^2}{\sigma_2^2}+\ldots+\frac{(x_n-\mu_n)^2}{\sigma_n^2} ]}}{(2\pi)^{\frac{n}{2}}\sigma_1 \sigma_2 \ldots \sigma_n}

其中，,,和,, 分别是第一维、第二维、的均值和方差。

给出严谨的定义以后，我接下来就用稍微生动一些的语言说一下这个回归：
简单来说就是我们在每一个取值都有一个对应的高斯分布，这个维度可能是许许多多维，然后，我们在其中通过大量的样本找出，最后回归成方程。这是我的理解，应该在组会上继续讨论。

  1. KL散度：
    1. 首先我们来解释一下熵的定义：
      熵，是信息论中最重要的指标，概率分布的熵的定义是：
H = - \sum_{i = 1}^N p(x_i)log_?p(x_i)

当我们使用log2时，可以将熵解释为“编码信息所需的最小比特数”
熵没有告诉我们如何实现这种编码，但我们可以通过熵来量化数据中所含有的信息，并且知道当我们将其替换为参数化的近似值时我们丢失了多少信息。

  1. 接下来介绍KL散度：
D_{KL}(p||q) = \sum_{i = 1}^Np(x_i)(log\frac {p(x_i)}{q(x_i)})

一般p表示观测值，q表示近似值

  1. 注意！KL散度不是距离，KL散度是不对称的！！！
  2. 为了使得信息丢失最少，可以选择KL散度最小的点

本文章使用limfx的vscode插件快速发布