神经网络基础

人工神经元

从人类神经元中抽象出的数学模型

1. 可总结为公式：
2. Threshold：激活函数

人工神经网络

大量神经元以某种连接方式构成的机器学习模型

第一个神经网络：perceptron（感知机）

\sigma (x)=\begin{cases}
1& \text{if x>0}\\
0& \text{otherwise}
\end{cases}

多层感知机

Multi Layer Perceptron(MLP)
单层神经网络基础熵引入一个或多个隐藏层，是神经网络有多个网络层：得名多层感知机

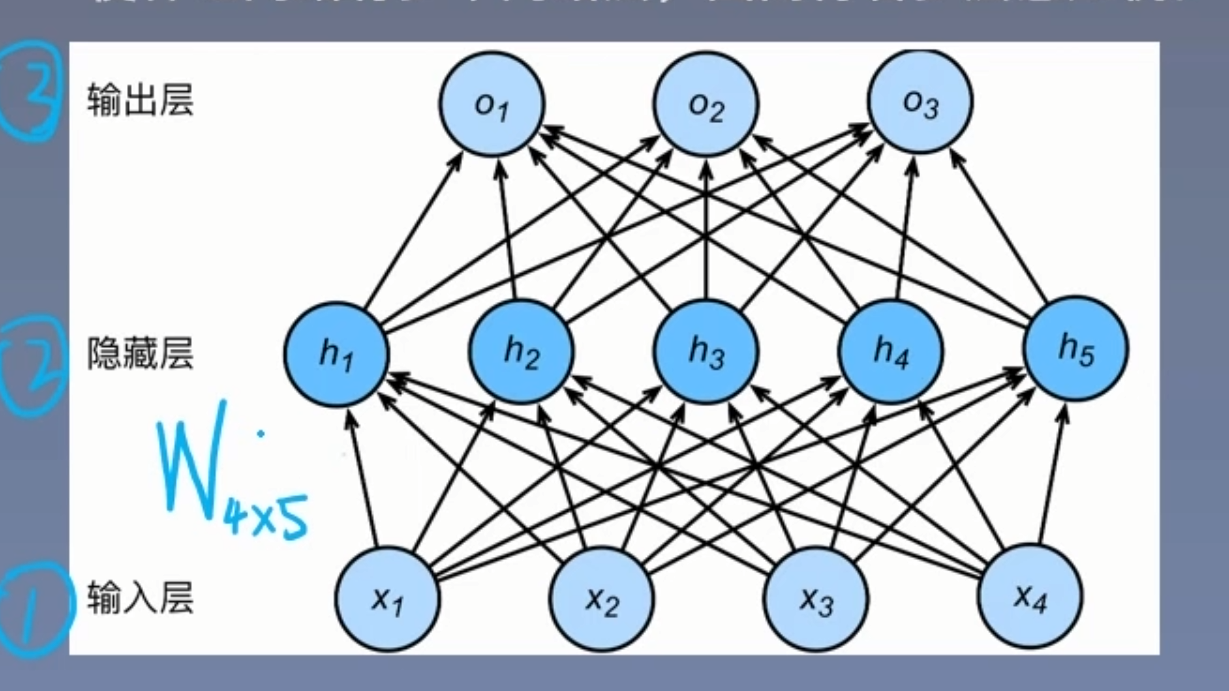
多层感知机前向传播

多层感知机的激活函数

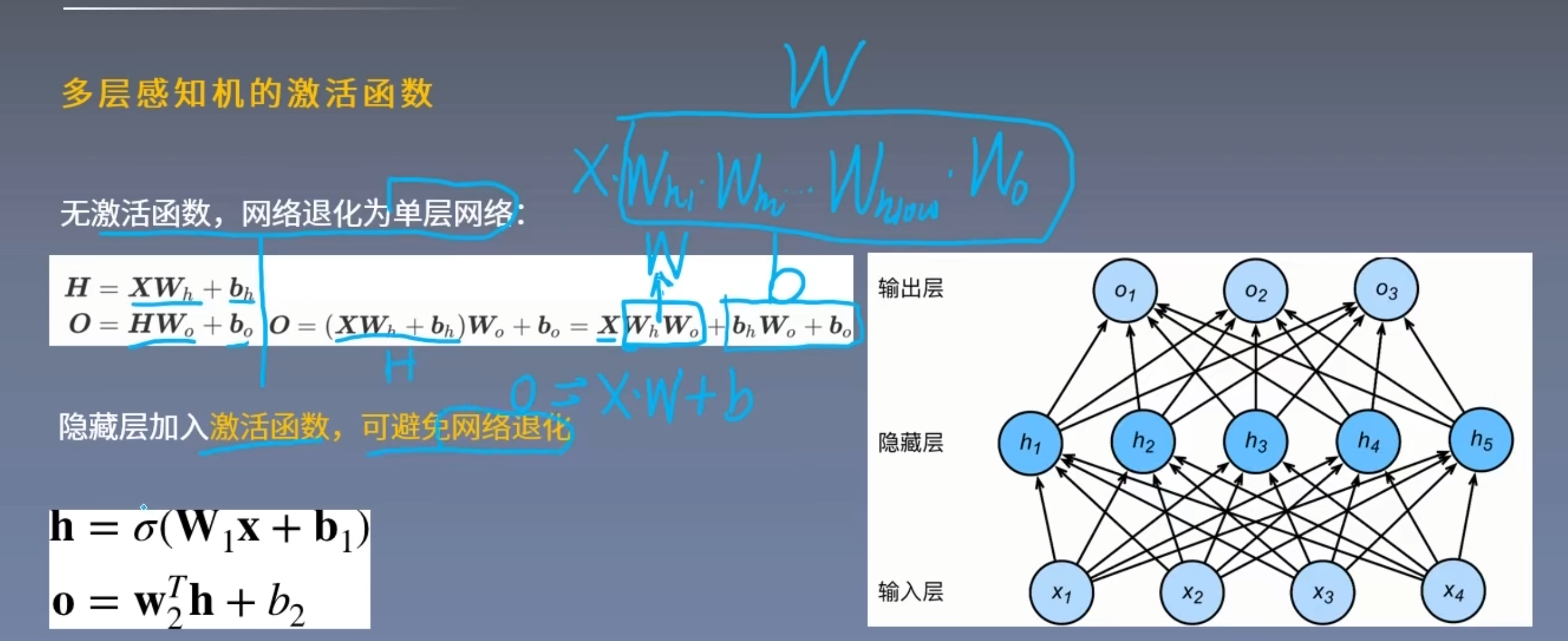
激活函数

1. 让多层感知机成为真正的多层，否则等价于一层
2. 引入非线性，是网络可以逼近任意非线性函数
3. 激活函数需要具备以下几点性质
   1. 连续并可导（允许少数点不可导），便于利用数值优化的方法
   2. 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率
   3. 激活函数及其导函数的值域要在合适的区间内，否则会影响效率和稳定性
4. 常见激活函数：

反向传播

1. 前向传播：输入层数据开始从前向后，数据逐步传递至输出层
2. 反向传播：损失函数开始从后向前，梯度逐步传递至第一层
3. 反向更新作用：用于权重更新，使网络输出更接近标签
4. 损失函数：衡量模型与真实标签的差异，
5. 反向传播原理：链式求导法则
6. 网络计算图
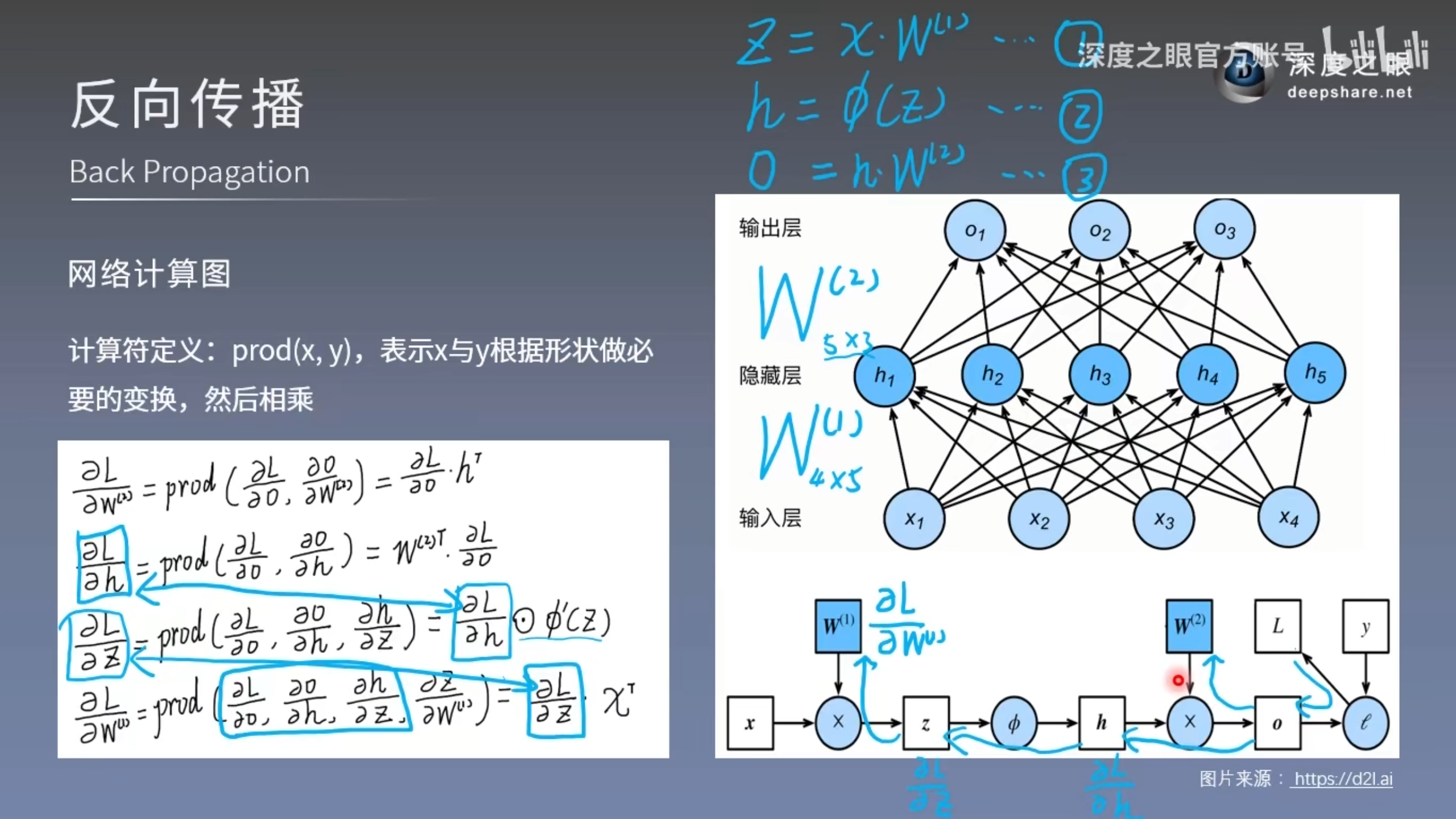
7. 梯度下降法：权值沿梯度负方向更新，使函数值减小

学习率

Learning Rate
控制更新步长

损失函数

衡量模型输出与真实标签之间的差距

1. Loss Function:单样本
2. Cost Function:总体均值
3. Objective Function:
4. 两种常见的损失函数

权值初始化

随机初始化法

高斯分布随机初始化，从高斯分布中随机采样，对权重赋值，如N（0，0.01）

自适应标准差

自适应方法随机分布中的标准差

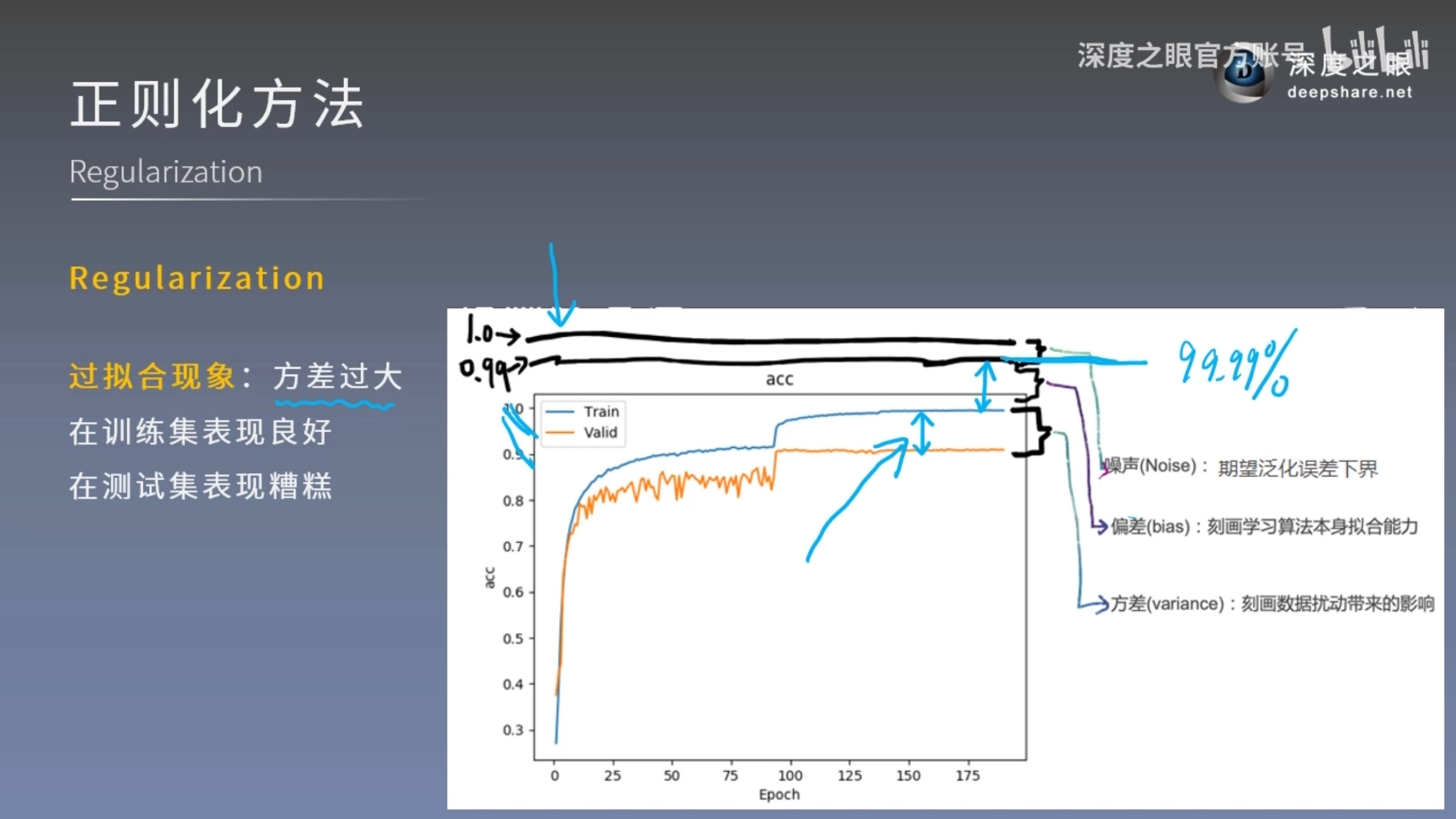
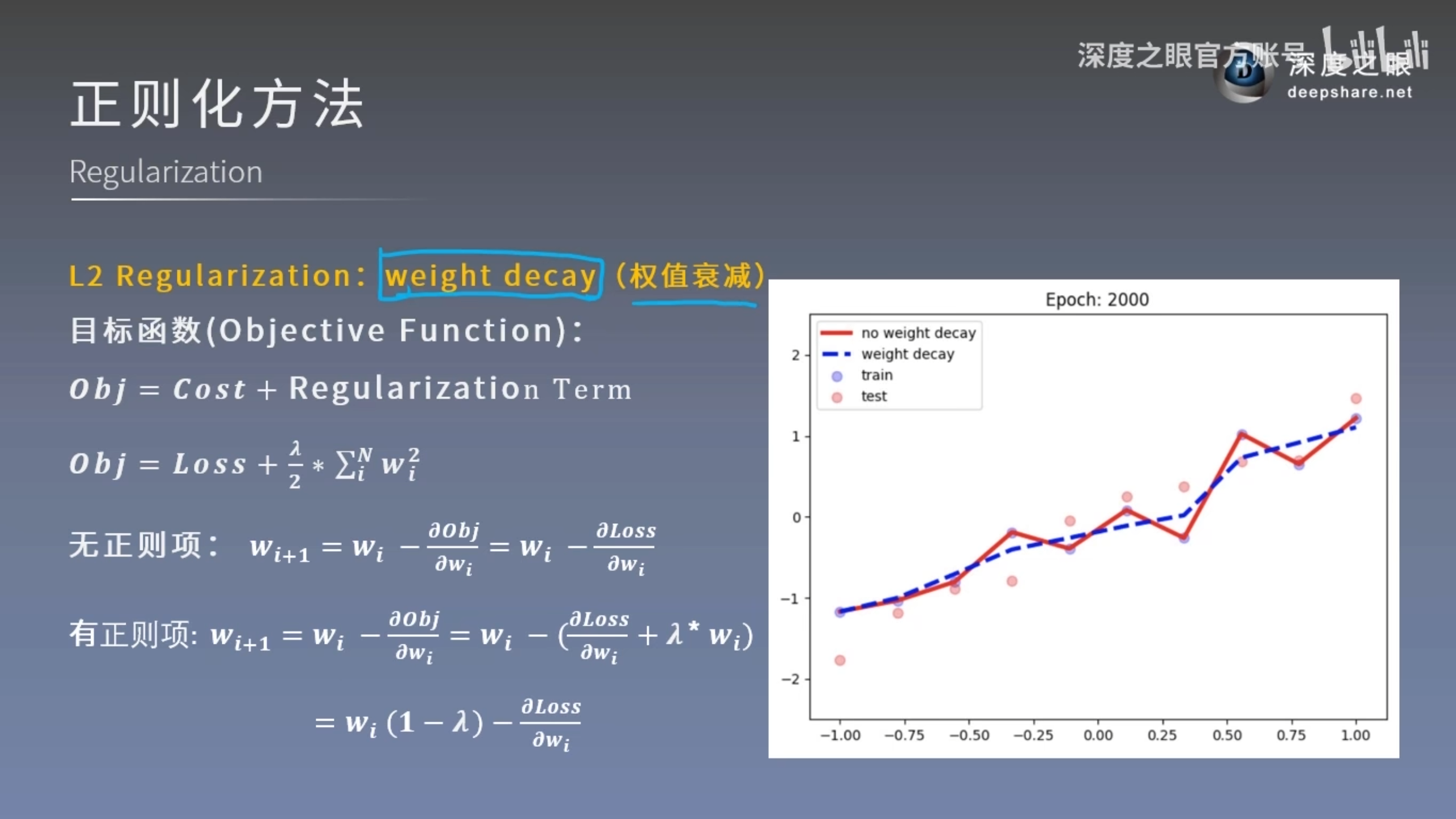
正则化方法

regularization
减少方差的策略，通俗理解为减轻过拟合的策略
误差 = 偏差 + 方差 + 噪声

1. 偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力
2. 方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所产生的影响
3. 噪声：表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界 注：L1为LASSO回归，L2为岭回归

---

本文章使用limfx的vscode插件快速发布