FitNetAPP

工具箱说明

• 本工具箱是基于 MATLAB 预测神经网络开发的工具箱，适用于：已知一组自变量和其对应的因变量，预测另一组自变量数据对应的因变量。
• 本工具箱基于 MATLAB 自带的 fitnet 类，对其建模、参数选择、模型分析过程进行了封装，生成了 FitNet 类。对 FitNet 类，设计了 APP 交互界面，将类的功能显示在界面上，方便使用。界面如下图所示：

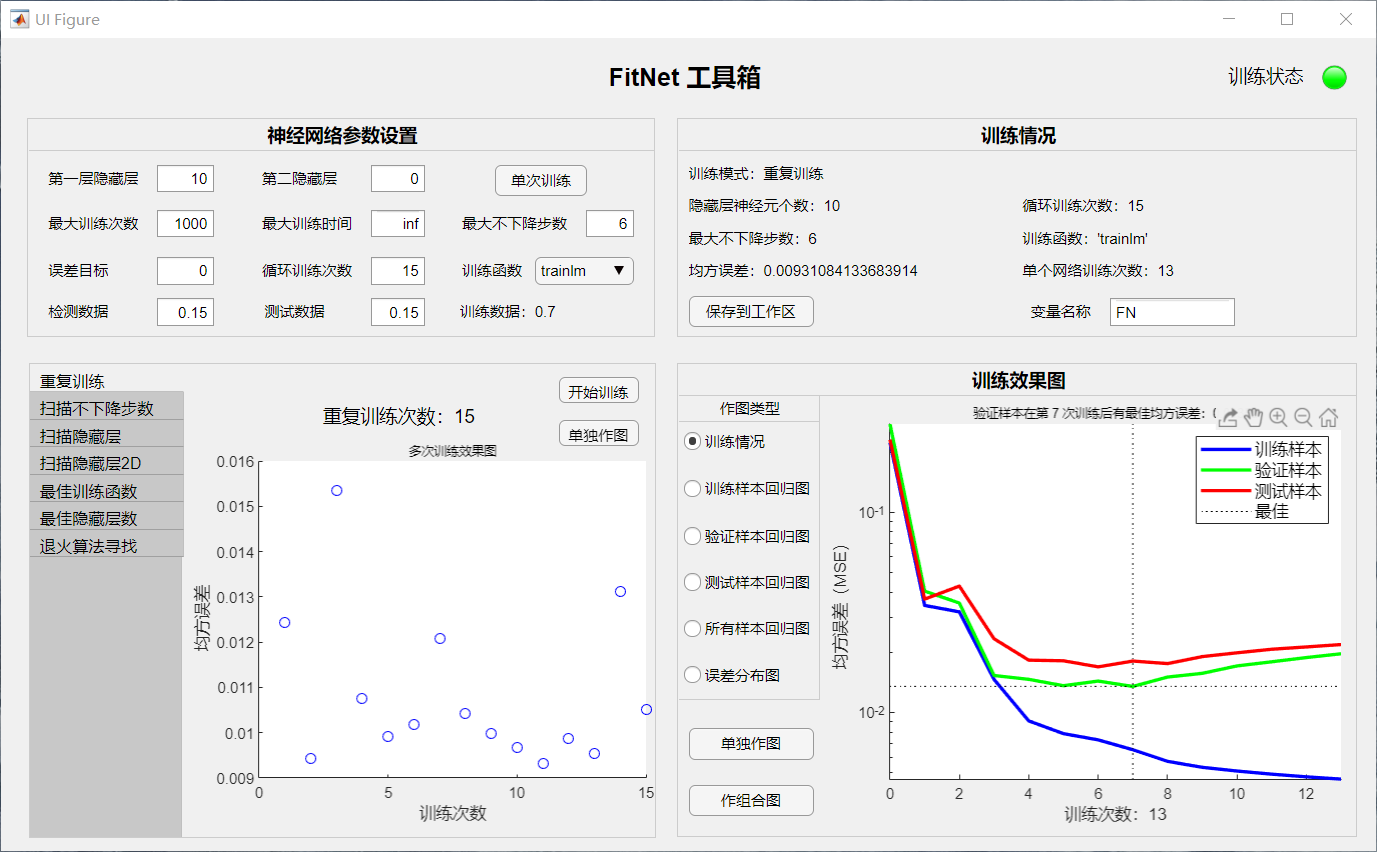
工具箱功能简介：

• 基本的参数设置、训练、作图分析功能（训练过程图、预测回归图、误差分布图）
• 循环训练多次，取最优值
• 在其他条件一定的情况下，更改训练函数、隐藏层神经元个数、最大不下降步数，以便寻找最好的训练函数。
• 运用简单的模拟退火算法，智能寻找上述三个参数的最优值。

APP 使用方法

打开APP

在命令行输入代码：

FitNetAPP(X,Y)

即可打开工具箱，其中 X 是已知自变量，每一行是一个样本，每一列是一个属性，Y是预测因变量，列向量。资源中有一个 mat 文件，里面包含了一个两组实验数据。X_little、Y_little 是数量较少的数据，X_large、Y_large 是数量较大的数据。

修改训练参数

在 APP 左上角面板中可以修改训练参数，

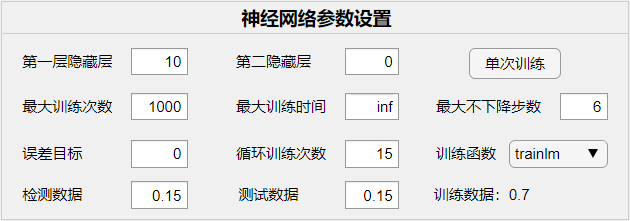
特殊说明：

• “第二层隐藏层数” 为 0 代表没有第二层隐藏层
• “循环训练次数” 是神经网络重复训练的次数，会取训练均方误差最小为最优解

参数扫描

• 在 APP 左下角面板中可以进行参数的扫描功能，以便选取合适的参数。
• 所有训练图可以点击 “单独作图” 生成独立的图窗。
• 在训练时，工具箱右上方指示灯为红，训练完成后为绿。
• 扫描参数时，每个参数下都会重复训练取最优值，所以为使训练时间不至于太大，应将循环训练次数设置比较小。MATLAB 命令行会显示训练进度。

所有模式的简介如下：

重复训练

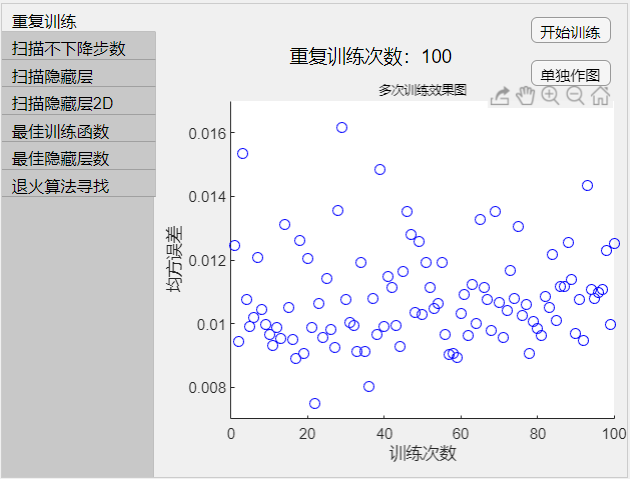
• 即在相同参数下重复训练，训练次数在参数设置 “循环训练次数” 中修改。
• 图示为训练次数与训练效果的散点图。

扫描不下降步数

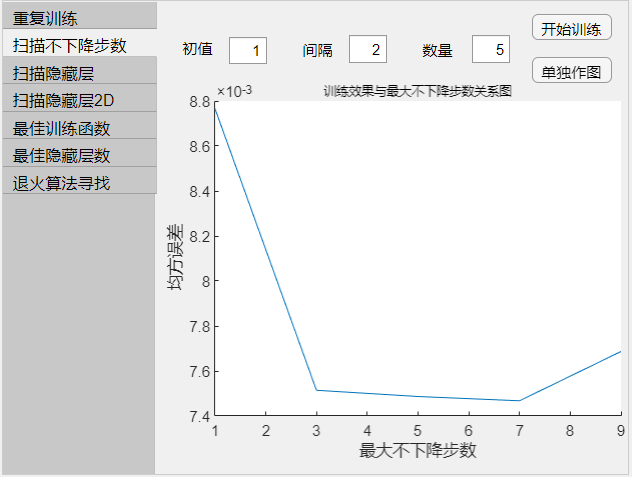
• 根据设置的 初值、间隔、数量 所代表的范围修改最大不下降步数进行训练。
• 图示为每个最大不下降步数下的训练情况图。

扫描隐藏层

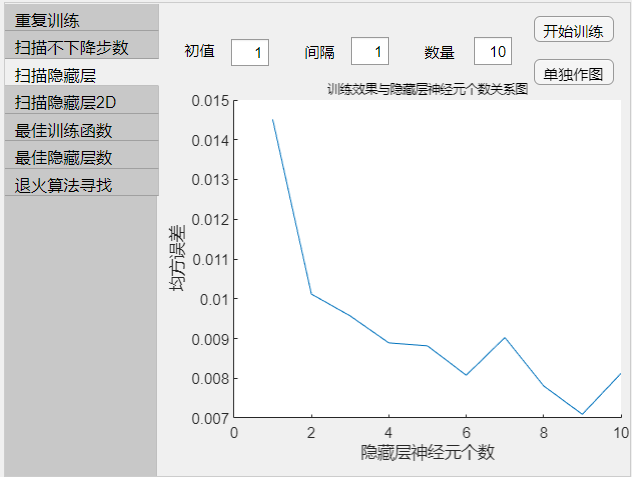
• 对一层隐藏层神经元个数进行扫描。
• 图示为每次训练产生的结果曲线图。

扫描隐藏层数2D

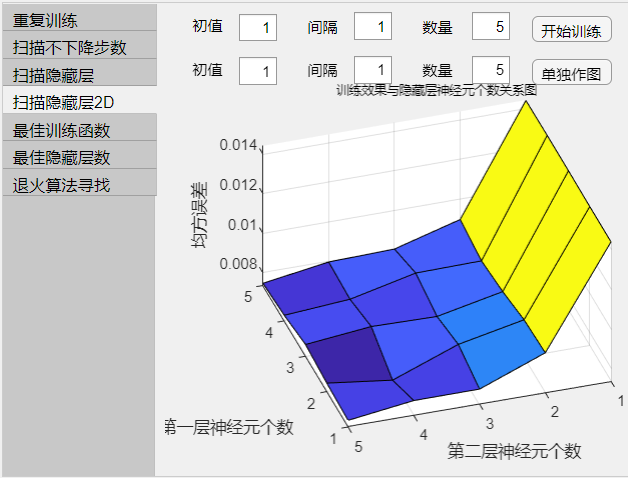
• 扫描两个隐藏层神经元个数对训练效果的影响
• 图示为两个隐藏层数和训练效果的三维图

最佳训练函数

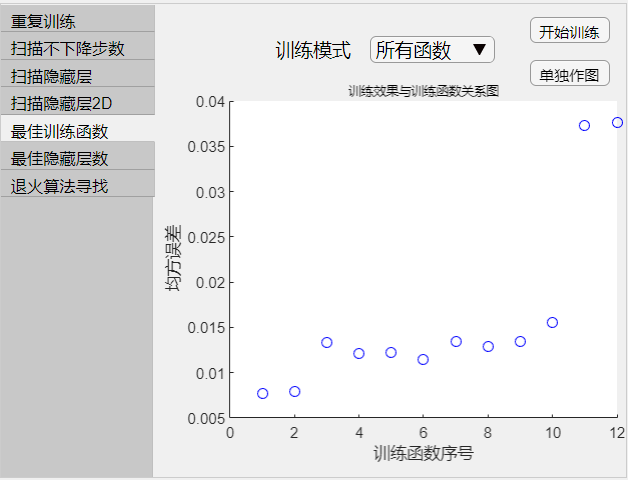
• 所有函数指扫描所有训练函数，常用函数指扫描常用的三个训练函数：trainlm、trainbr、trainscg
• 扫描顺序与参数设置中训练函数下拉列表顺序相同
• 图为每个训练函数训练效果散点图

最佳隐藏层数

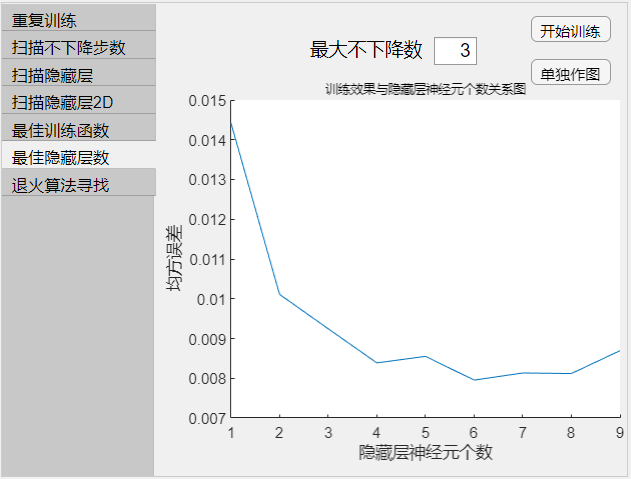
• 最大不下降步数：隐藏层神经元数从 1 开始递增，当神经元数增加但训练效果不如当前最佳值，称为一次不下降步数，当不下降步数达到最大不下降步数时，停止训练。
• 图示为每次训练结果图

退火算法寻找

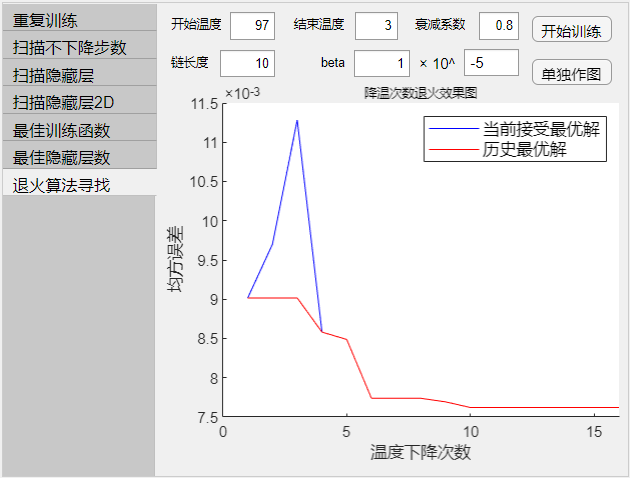
• 设置模拟退火参数，用模拟退火算法对隐藏层神经元数、最大不下降步数、训练函数进行选取。
• 需要有模拟退火算法基础。
• 图为模拟退火算法的检验图。

结果显示

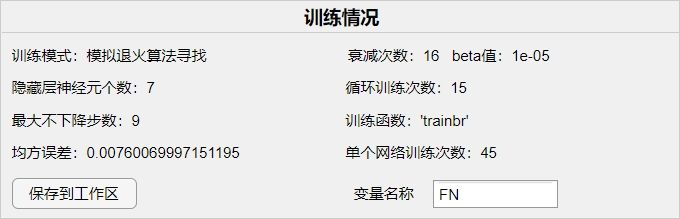
训练的参数、结果将会显示在 APP 左上方。

模型分析

在 APP 右下方有模型的作图分析。

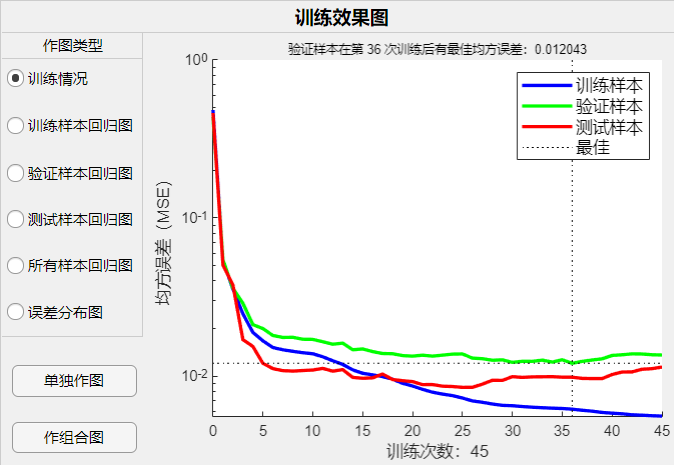
左侧单选框可以选择预览，单独作图可以在独立图窗中显示，作组合图生成三个效果分析图，如下所示：

训练过程图

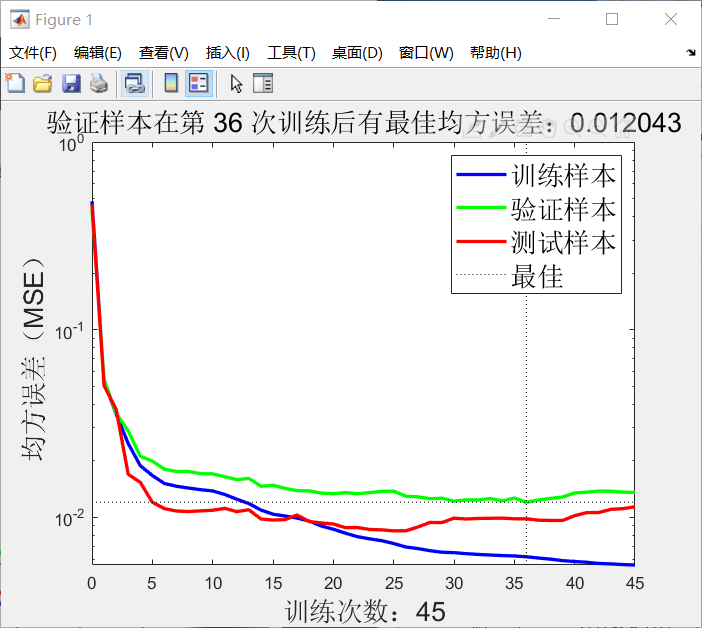
记录了最优神经网络在训练过程中随着每一次训练样本均方误差的变化。最佳次数指验证样本均方误差最小。由于训练是拿训练样本训练，即训练样本均方误差会一直减小，但是随着训练加深，很有可能模型偏离了普遍样本的特征，即 “过拟合”，此时验证样本均方误差反而会增加。当连续增加设置的 “最大不下降步数” 后训练停止。

预测回归图

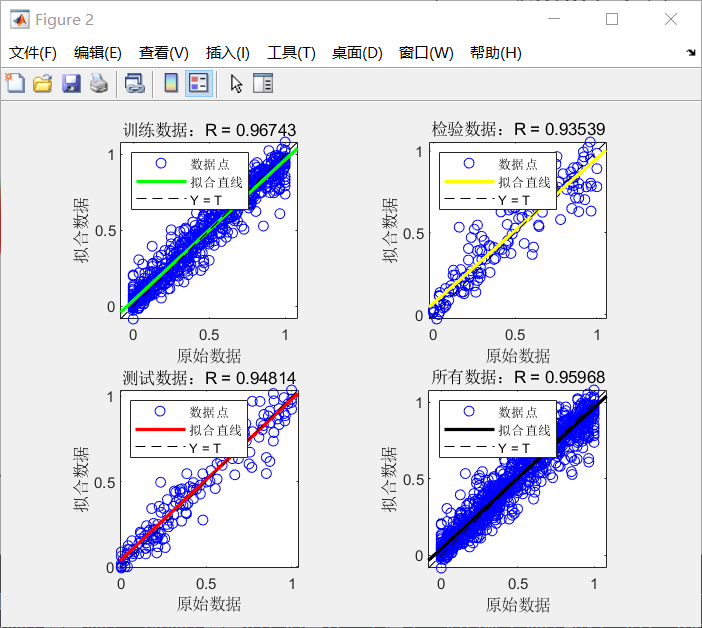
如图为三个样本数据的拟合回归图。横轴为原始数据值，纵轴为预测数据值。如果拟合值和原始值完全相同，则散点会全部在直线 y=x 直线上。当出现误差，则会偏离这条直线。R 为所有的散点的线性相关系数，线性相关系数越接近 1 说明效果越好。

误差分布图

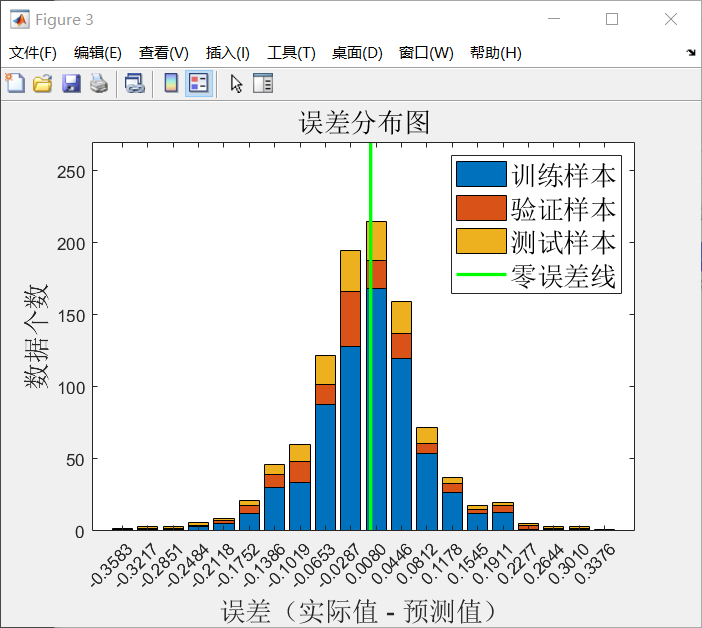
即误差的分布条形图。

运用模型进行预测

在模型训练完成后，运用模型进行预测。

首先在右上方 “训练情况” 模板中设置变量名称，点击保存到工作区，即可将类保存到工作区。

然后用 sim 函数即可预测：

Ynew = FN.sim(Xnew);

FN 为变量名称，Xnew 为新数据的自变量，每一行为一个样本，每一列为一个属性。

输出 Ynew 即为预测结果，列向量。

本文章使用limfx的vsocde插件快速发布