机器学习概述

什么是机器学习？

为了了解什么是机器学习，我们不妨先思考一下在不用机器学习的情况下，我们一般在解决问题的时候，会怎么做呢？
一般会分为一下三步：

• 将问题量化

• 建立数学模型

• 根据数学模型进行编程求解

可以很明显的发现，这两步中，一般第一、二步是由人类完成的，而第三步是由机器完成的。为什么呢？因为以前一般认为，机器不具备自己从问题中建立数学模型的能力，所以一般只在建立完数字模型之后帮忙进行运算。
也就是说，过去的解题过程中，解题思路其实是人类给出的，机器只是帮忙运算了而已。
接着，一种理论改变了这一切。它就是机器学习。
机器学习，就是一种能让机器自行学习的方法。利用各种数学理论，能够让机器从问题的数据中自行学习，并建立数据模型。也就是说这种理论出现后，人只需要进行量化问题的工作就行了，剩下的机器可以自行完成。

机器学习的原理

看到这里，很多人可能会很好奇，是用什么办法让机器可以像拥有思维了一样，能自行学习了呢？
其实其数学原理很简单，而且正好是你们大一下在微积分中刚学过的内容：梯度下降。
设想一下一个问题，我们将其量化后变成一个复杂函数的拟合问题。这个问题的量化结果为我们提供了以下的数据：

• 不同输入（可多个）

• 对应的实际输出

那么，我们使用一个函数来拟合它。我们先随便设定一个足够复杂的多项式函数，随机初始化它的各项系数。然后，我们设定一个拟合过程，在每一步拟合中，我们：

• 代入真实输入，计算我们的函数的输出

• 使用差别函数量化我们的输出和实际输出的差别（即loss）（比如直接相减）

• 我们把拟合函数的各项系数当作自变量，这样loss实际上就是一个函数

• 计算这个函数的梯度，用反向梯度乘以预设的学习率，然后以此值更新各项系数，这样函数实际上在向让loss变小的方向变化

• 多次重复以上过程

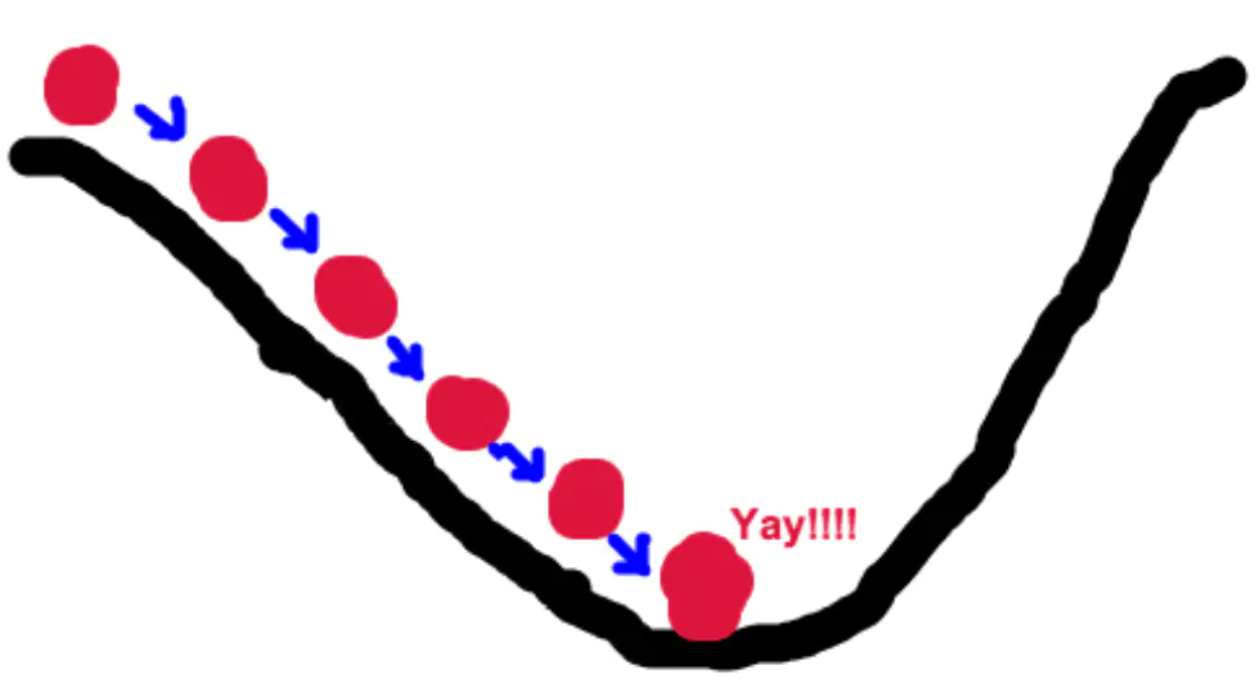
最后，loss会趋近于0，此时函数就拟合完毕了。
用网上盗的一张图来表示过程就是：

这个过程就叫梯度下降。
所以，理论上只要能构造出比问题更复杂的函数，就能用梯度下降完全拟合求出这个问题的解。
那么如何构造这个拟合函数呢？

梯度下降与神经元

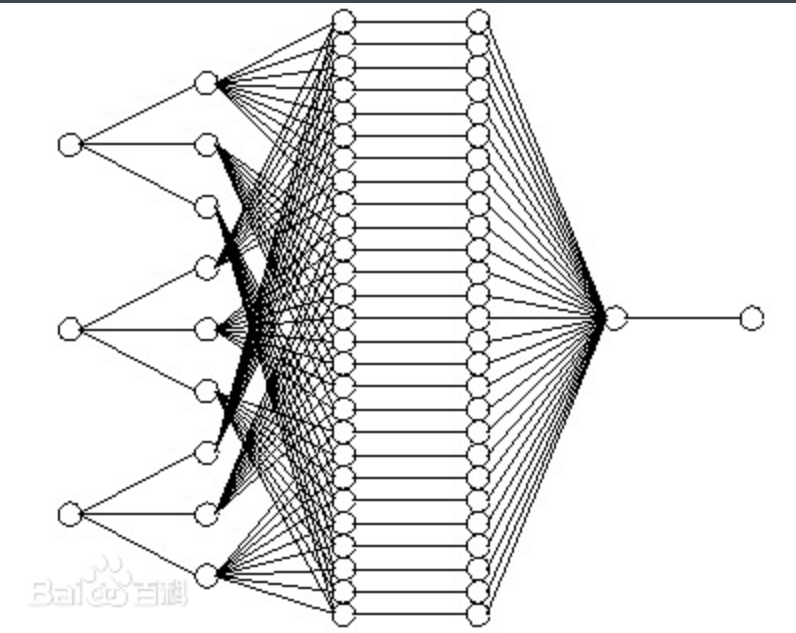
科学家从人脑中找到灵感，使用神经网络结构来构造复杂函数。

这就是一个神经网络，里边每个节点是一个神经元。神经元实际上是一个线性算式

\[ y=w\times{x}+b \]

这样，可以轻松地通过堆积神经元获得复杂的函数。但是单纯地堆积神经元是有问题的：

• 无论堆积多少神经元，最终拟合的函数始终是线性

所以，我们经常在每个线性层后边加入非线性的激活函数，赋予其一些非线性特征。主流的有relu,sigmoid函数等等。同时，我们也有很多其它的非线性神经元。

机器学习的局限性

尽管机器学习看起来十分高级和强大，但他并不是万能的，甚至很多时候都不是解决问题的最佳方法。
注意机器学习的本质，是机器代替了人类进行模型的建立。而如果人类已经用数学方法证明、找到了完美的数学模型，那么其效果必然远好于机器学习。机器学习的本质是函数逼近，逼近不可能完全达到原本的真正模型的效果。
机器学习的使用方法，应当是能不使用就不使用，切勿为使用机器学习而使用机器学习。机器学习的发明是用于解决靠人类无法完成建模的问题，不是用来解决人类可以进行数学建模的问题。几年前曾经有个推荐算法比赛，最终的冠军算法是基于相似客户的浏览历史进行推荐，非常简单，效果比一批机器学习算法好一大截。
并且机器学习极其依赖数据。尽管现在有一些机器学习算法不怎么依赖数据，但是那是特殊情况。大部分的优秀机器学习成果是都是通过大数据堆出来的，而优质数据个人往往难以入手。
希望大家在学习的时候牢记上方这几点，不要在未来觉得它有时候鸡肋、用不上而放弃。

---

本文章使用limfx的vsocde插件快速发布