数据科学入门1.4:多变量回归
Introduction to Data Science Part1.4: Multi variable Regression
多变量回归
之前我们讲了一个independent variable的情况,那如果有多个x怎么办, 如下面的例子:
exp3 这是一群人年收入,高中毕业以后受教育的年数,和信用卡账单,我们想通过前两个来预测他一年花多少钱。
Annual Income x1 | # Years Post-High School Education x2 | Annual Credit Card Charges y |
|---|---|---|
$39,400 | 5 | $10,120.45 |
$68,200 | 4 | $15,289.80 |
$43,000 | 6 | $5,937.19 |
$53,600 | 2 | $0.00 |
$53,500 | 4 | $13,569.89 |
$60,800 | 2 | $3,889.79 |
$74,900 | 1 | $7,715.47 |
我们还是老方法
%% get a glance of the data
scatter3(exp3.x1,exp3.x2,exp3.y)
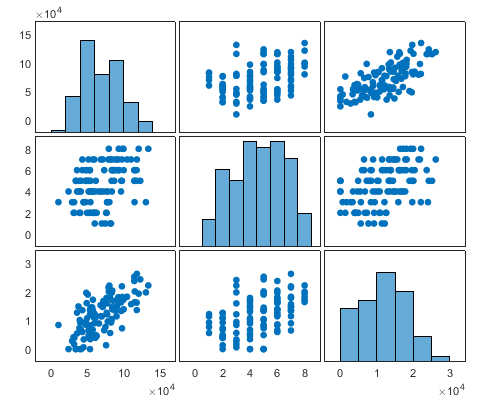
plotmatrix(exp3.Variables)
%% fit a surface
[model,gof,output]=fit([exp3.x1,exp3.x2],exp3.y,"poly33")
plot(model,[exp3.x1,exp3.x2],exp3.y)
%% let's look at the result
% this shows the goodness of the fit
gof
% let's plot the residuals
scatter(exp3.x1,output.residuals)
scatter(exp3.x2,output.residuals)
histogram(output.residuals,10)
model
gof
首先我们还是把图画出来看看,这个叫做exploratory data analysis,探索新数据分析,看看大概数据是啥样。可以看到除了散点图我还画了一个图plotmatrix(exp3.Variables),这个可以把表格里面所有变量两辆话在一个散点图中,如下面 :
这个图是对角线对称的,大的xy周分别是变量,对角线就是自身对自身没必要画散点图,就给出了分布的直方图。我们关心的是那两个变量之间有关系。可以看到x1,和y有比较明显的正相关,你们希望看到的是independent variable和dependent variable之间有相关而independent variable之间最好没有,这样说明每个变脸都是独立有作用的。如果independent variable之间强有相关则可以去掉某个变量。我们便量少可以不管,当independent variable多的时候尽量选择和Y关联大的之间没关系的变量。
再看fit模型,我们只关注有什么变化,首先是fit里面"ploy33",因为我们有2个independent variable,所以我们对两个都采用3次多项式,你也可以尝试别的不同的玩法。你可以看到这个residual的plot我们也有两个。
更多变量回归
我们之前一直在用fit,fit是curve fitting toolbox里面的玩意,用起来虽然简单但是还是功能比较悠闲的,比如independent variable超过2个就不能用了,怎么办呢,我们还有statistic and machine learning toolbox。其中有东西叫做fitlm,应该是fit linear model的意思我们开看看他。
exp4 这个是年龄,血压,是否吸烟和未来10年发生中风的概率的关系,现在让你预测一个人是否未来会发生中风。
Age x1 | Blood Pressure x2 | Smoker x3 | % Risk of Stroke over Next 10 Years Y |
|---|---|---|---|
63 | 129 | No | 7 |
75 | 99 | No | 15 |
80 | 121 | No | 31 |
82 | 125 | No | 17 |
60 | 134 | No | 14 |
79 | 205 | Yes | 48 |
79 | 120 | Yes | 36 |
我们看下面一个代码:
%% transform yes/no to 1/0
[index,~,isSmoker]=unique(exp4.x3)
isSmoker=isSmoker-1
%% fit a simple 1 degree polynomial model
ft=fitlm([exp4.x1,exp4.x2,isSmoker],exp4.y)
%% you can specify the order of the polynomial model
T=[1 0 0 0;...
0 1 0 0;...
0 0 1 0;...
1 1 0 0;...
1 2 0 0;...
3 0 0 0;...
0 0 0 0]
ft=fi
首先,我们要把表格里面的yes/no变成1/0,这样才能用计算,非常简单用unique函数,大家不懂可以查查,出来以后吗默认是吧不同种类的字符串变成了从1开始的数字,我们未来方便剪掉1,这样抽烟就是1,不抽是0。这个是一个很基础的数据预处理,当然如果你的一个数据有很多种类型,直接的用1,2,3...这种编码其实是不合适的,可以使用one hot编码,这个大家自己去研究,下次可也会讲。
预处理之后只要用fitlm指定independent variable和dependent variable就行。可以看到他的给出的模型是:
ft =
线性回归模型:
y ~ 1 + x1 + x2 + x3
估计系数:
Estimate SE tStat pValue
________ ________ _______ __________
(Intercept) -72.508 15.092 -4.8043 0.00010793
x1 0.83483 0.16446 5.0761 5.7719e-05
x2 0.22801 0.048995 4.6539 0.00015295
x3 10.607 3.2056 3.3089 0.0035044
观测值数目: 24,误差自由度: 20
均方根误差: 6.53
R 方: 0.824,调整 R 方 0.798
F 统计量(常量模型): 31.3,p 值 = 9.43e-08
居然是中文的真不习惯,可以看到y~那一串就是模型的公式,然后那个estimate就是系数。R 方: 0.824,调整 R 方 0.798就是我们之前说的rsquare和adjrsquare。这次多了个东西,就是pValue,这个表示这个参数是否在统计学上significant。这里一时半会解释不清,挺复杂,你就认为这个数字小于0.05这个参数对应的independent variable就是有意义的,要是比这个大,就代表可以忽略掉他,你再做个模型就不要加这个变量了。
这里再说一点,就是你看这个模型的参数,isSmoker的系数最大时10多,说明只要吸烟你中风的概率比别人搞10%,这也是我们从模型中可以总结出来的规律。
到这里你要说,这个虽然是实现了多变量的回归,但是是一次多项式呀,怎么变成更高次的呢?,简单如下面这个代码:
%% you can specify the order of the polygonal model
T=[1 0 0 0;...
0 1 0 0;...
0 0 1 0;...
1 1 0 0;...
1 2 0 0;...
3 0 0 0;...
0 0 0 0]
ft=fitlm([exp4.x1,exp4.x2,isSmoker],exp4.y,T)
就是加一个参数叫Terms Matrix,这个用来指明你模型中的阶数,很好理解,每一行就对应一项,而每一列对应每个independent variable的阶数,如第一行 1 0 0 0,对应的就是 \({x_1}^1*{x_2}^0*{x_3}^1\) ,最后一个0是必须的不知道为啥。那么底5航1 2 0 0对应的就是 \({x_1}^1*{x_2}^2*{x_3}^0\) 。你不用吧每一行都写完,你要用几个就写几行,上面这个模型结果如下:
ft =
线性回归模型:
y ~ x3 + x1*x2 + x1:(x2^2) + x1^3 + 1
估计系数:
Estimate SE tStat pValue
___________ __________ ________ _________
x1 -0.23256 1.3909 -0.1672 0.86919
x2 0.12519 0.42139 0.29709 0.77
x3 10.643 3.4187 3.1132 0.0063233
x1:x2 -0.00095897 0.0080442 -0.11921 0.9065
x1:x2^2 7.4576e-06 2.4488e-05 0.30454 0.76441
x1^3 6.8769e-05 7.5166e-05 0.91491 0.37304
(Intercept) -9.332 87.015 -0.10725 0.91585
观测值数目: 24,误差自由度: 17
均方根误差: 6.9
R 方: 0.833,调整 R 方 0.774
F 统计量(常量模型): 14.1,p 值 = 8.89e-06
可以看到这个rsquare增加了,但是adjrsquare没有,所以我们增加了个个模型的复杂度,但是并没有增加什么有意义的项,你看有好几个pValue都很大。
这里你又要问了,这里只能用多项式拟合,我像自定义一个模型的公式可以吗?当然是可以,我以前教过你的对吧。只要线性回归你总能把你的模型携程 \(af(X)+bg(X)...\) 这种形式对吧。
例如: ft=fitlm([sin(exp4.x1),exp4.x2,isSmoker],exp4.y)
本文章使用limfx的vsocde插件快速发布