数据科学入门1.6:简单时间序列预测与总结
Introduction to Data Science Part1.6: Time Series and Sumary
时间序列与ARIMA模型
刚才我们都是用几个independent variable x来与的dependent variable y。x和y都属于一次观测。如果我们只有一个变量就是y本身,然后不停的一次接一次的观测y,得到一个序列,然后我们想要预测未来的y值怎么玩呢?例如我们有一支股票他几个月以来每一天的收盘价,我们想预测明天的股票价格。
首先我们定义一下这个模型。对于一个随机事件,我们每个一段时间观测一次,或者每隔一段时间按顺序发生的一个随机事件,我们叫他随机序列。对于第t次观测值,我叫做 \(y_t\) ,前一次就叫做 \(y_{t-1}\) ,前一次的前一次叫做 \(y_{t-2}\) ,那么 \(y_{t-k}\) 能够理解了吧。
我们首先搞个简单的模型叫线性自回归模型(auto-regressive model)
\[ y_t=c+\sum_{i=1}^{k}\beta_i*y_{t-i}+\epsilon \]
这个能看懂吧,就是下一个y的观测值=之前k次的观测值的线性组合+上一个随机的误差。这个模型你想想你用我们之前学的知识可以做吧。这个就是表现了未来的值,和历史值有关。
ok我们现在学一个更加复杂也是实际中用的更多的一个模型叫做ARIMA(auto-regeressive integrated moving average)。我这不是数学、也不是统计学课,我不将太复杂,但是我觉得基本的远离还是要熟悉一下:
一个ARIMA模型的表达式是(我移动了一下你们看着简单点):
\[ y_t^d=c+\sum_{i=1}^{p}\beta_iL^iy_t^d+\sum_{i=1}^{q}\theta_iL^i\epsilon_t \]
先讲几个算子:
lag算子:超简单就是 \(L^iy_t=y_{t-i}\)
d差分算子:\(y_t^d\) y的d阶差分,d=1是 就是 \(y_t-y_{t-1}\),d是2的时候就是 \((y_t-y_{t-1})-(y_{t-1}-y_{t-1})\),简单吧。
I是integrated的意思,就是这个模型是加起来用的,他预测的是y的差分也就是y的变化量,并不直接是y。为什么这么做呢,他是为了让模型不受trend和seasonal分量的印象。trend就是数据在时间上有个趋势,例如房间年年涨,这种。seasonal就是周期新的分量,例如每年夏天电费都素会比其他季节高。去掉了他们的影响,我们的模型才不受时间的影响,不会说上半年能用下半年就不能用了。这个就叫做模型是Stationary的。
前面和y有关的就是各个说过的AR模型。
那MA是什么意思呢?Moving Average的意思就是后面$\left(1+\sum_\theta_iLi\right)\epsilon_t$这一项代表一个moving average模型预测与之前观测数据误差的一个线性组合。它代表了一个未知扰动量对未来值得影响。
这个ARIMA模型实际上最早是来自于金融领域,说白了就是为了预测股票价格的。我们再看看AR,他表示的就是前几天得行情与明天行情得关系,前几天的行情,是我们可以观测得量。同时后面MA得部分,代表一个扰动,原文叫做“shock”,这一部分是我们无法直接观测的,只能通过他对y得印象来推测。例如突然发证了地震,或者病毒疫情导致股票下跌,在ARIMA模型模型中,是没有地震和疫情这个变量输入的,但是他们的影响在MA那一部分通过前几次的误差得线性组合被考虑了。
为什么搞得这么纠结,当然是应为这样一般情况下更准一些,一本模型越复杂拟合的越好,你要记住的是p,d,q这3个超参数(我们后面会讲什么是超参数)。p是AR部分阶数,就是和过去几次观测有关,q是MA部分的阶数,就是和过去几次扰动有关,d是差分阶数,我们一般=1就可以了。
好的我们做个例子,如我们
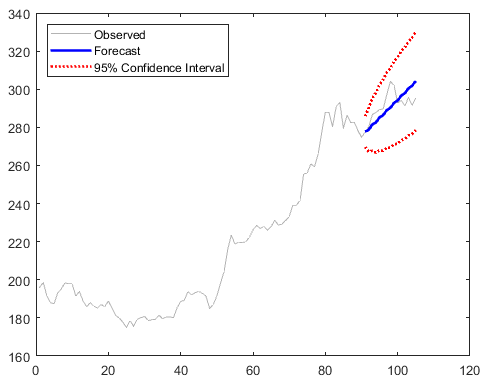
exp7 这里给出谷歌5个月的股价,我们来预测看看。
%%fit the model
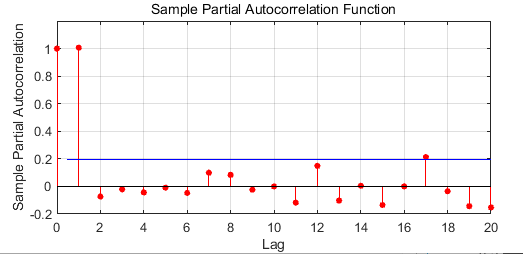
parcorr(exp7.price)
Mdl = arima(2,1,2);
model=estimate(Mdl,exp7.price(1:90))
%% forcast
[pred,ymse]=forecast(model,15,exp7.price(1:90))
% just plot
h1 = plot(exp7.price,'Color',[.7,.7,.7])
hold on
h2 = plot(91:105,pred,'b','LineWidth',2)
h3= plot(91:105,pred + 1.96*sqrt(ymse),'r:',...
'LineWidth',2);
plot(91:105,pred - 1.96*sqrt(ymse),'r:',...
'LineWidth',2);
legend([h1 h2 h3],'Observed','Forecast',...
'95% Confidence Interval','Location','NorthWest');
hold off
首先我们先用parcorr这个函数看看,当前股价和过去几天的股价有没有什么关系,可以看到t-1和体关系很明显,后面的就不是很明显了,所以我们模型的p可以选1-2就够了,d一般都是选1,q的话和p选差不多一本也不错,其实p可以通过调用autocorr看在哪里cutoff来判断,不过这个数据不是很好参考意义不大。
然后我们调用estimate来fit我们的模型。我这里要吐个槽,matlab不同工具箱,差不多的东西风格差异很大,这好蠢。我们用1-90填的数据来预测,再用forecast来预测,我们直接预测之后15天的股价走势。看看预测的还是挺准的。这个forecast返回两个东西,一个是预测值,实际上是一个期望值,还有一个是这个期望值对应的variance,然后你可以通过*1.96得到95%的置信区间,就是这个模型给出的分布,95%的概率在这+-1.96 * variance范围内。
VARM 模型 Vector Autoregression Models
各个讲的那个ARIMA模型,它适用的时单个变量的数据,有时候一个时间序列它包含了多个变脸怎么办呢?
例如下面这个例子:
exp8: 他给出了一个风力发电厂几年来每10分钟一次的数据,包括风速风向、理论课发电量和实际发电量,4个变量。假设我们想预测实际发电量,实际上另外3个变量对他也是有用的,实际上预测某一个变量,其他的可能都用得上。其实和之前的auto regression模型基本上没区别是不过换成了向量,协议这种叫Vector auto regression(VAR),公式和之前是一样的,就是认为Y,和参数都是向量就行:
\[ Y=C+\sum_{i=1}^{p}\Beta_i*L^iY+\Epsilon \]
我们再matlab里面用下免得代码建立一个VAR模型
model=varm(4,lag)
当我们fit了这个模型以后,会发现它给除了下面的参数:
model =
varm - 属性:
Description: "4-Dimensional VAR(20) Model"
SeriesNames: "Y1" "Y2" "Y3" ... and 1 more
NumSeries: 4
P: 20
Constant: [4×1 vector of NaNs]
AR: {4×4 matrices of NaNs} at lags [1 2 3 ... and 17 more]
Trend: [4×1 vector of zeros]
Beta: [4×0 matrix]
Covariance: [4×4 matrix of NaNs]
我们的公式就是:
\[ \hat{Y}=C+\sum_{i=1}^{p}AR_i*L^iY+ \sum_{i=1}^{p}\Beta_i*L^iX+\delta*T \]
C就是Constant,AR时几个n*n的矩阵,n就是Y的元素个数,B和AR差不多,他是X的参数,X时外因变量,就是会影响Y但是我们不预测他,T时一个trend,是一个趋 势,就是一段平均值。
更多的可以参考: https://www.mathworks.com/help/econ/model-specification-structures.html#bswxr8u-19
https://www.mathworks.com/help/econ/introduction-to-vector-autoregressive-var-models.html#bswxr8u-2
这里给大家不吱个课堂作业,就是上面这个立体我没有给出完整的解答,大家可以尝试做一下,预测效果有限,大家可以尝试不同的玩法,看看谁的准。有一个提示,就是VAR这种模型是线性的,属于很简单的模型,这里提供的数据是远远超过了这个模型需要的。
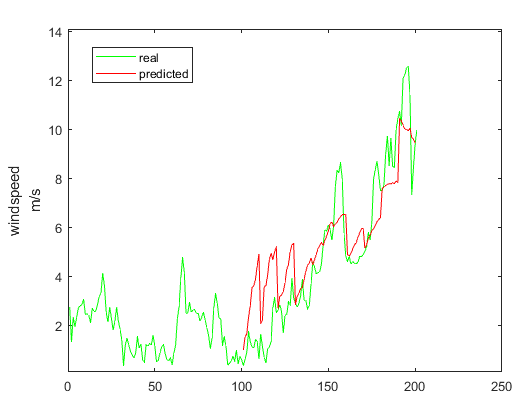
下面是我预测的风速:
总结
ok各种简单的回归我们都学完了总结一下:
首先如果可以把数据plot出来看看是什么规律,这个叫做exploratory data analysis,探索新分析
选取是特征并作为independent variables,那些是目标dependent variables
然后根据前面探索的结果选择采用什么样的模型公式,一般情况下,简单的线性回归,多项式就可以了,如果你想不出来更好的就用这个原则。
然后调用fit函数fit你的样本,得到一个模型。
看看模型的adjrsqure,plot出来残差图,没啥问题的话就ok了。
用模型的predict方法来预测吧。
本文章使用limfx的vsocde插件快速发布