静气动弹性力学涉猎
1 绪论
静气动弹性力学的领域是研究由定常流引起的气动载荷和由此产生的升力面结构弹性变形之间相互作用下飞行器现象。其对结构变形速率和变形加速度不敏感。主要包括两类问题:一、气动载荷对弹性变形的影响,弹性变形对气动载荷的影响;二、升力面结构潜在不稳定性(机翼发散)。
涉及知识:空气动力学、材料力学、理论力学、高等数学
2 风洞模型
2.1 洞壁安装模型
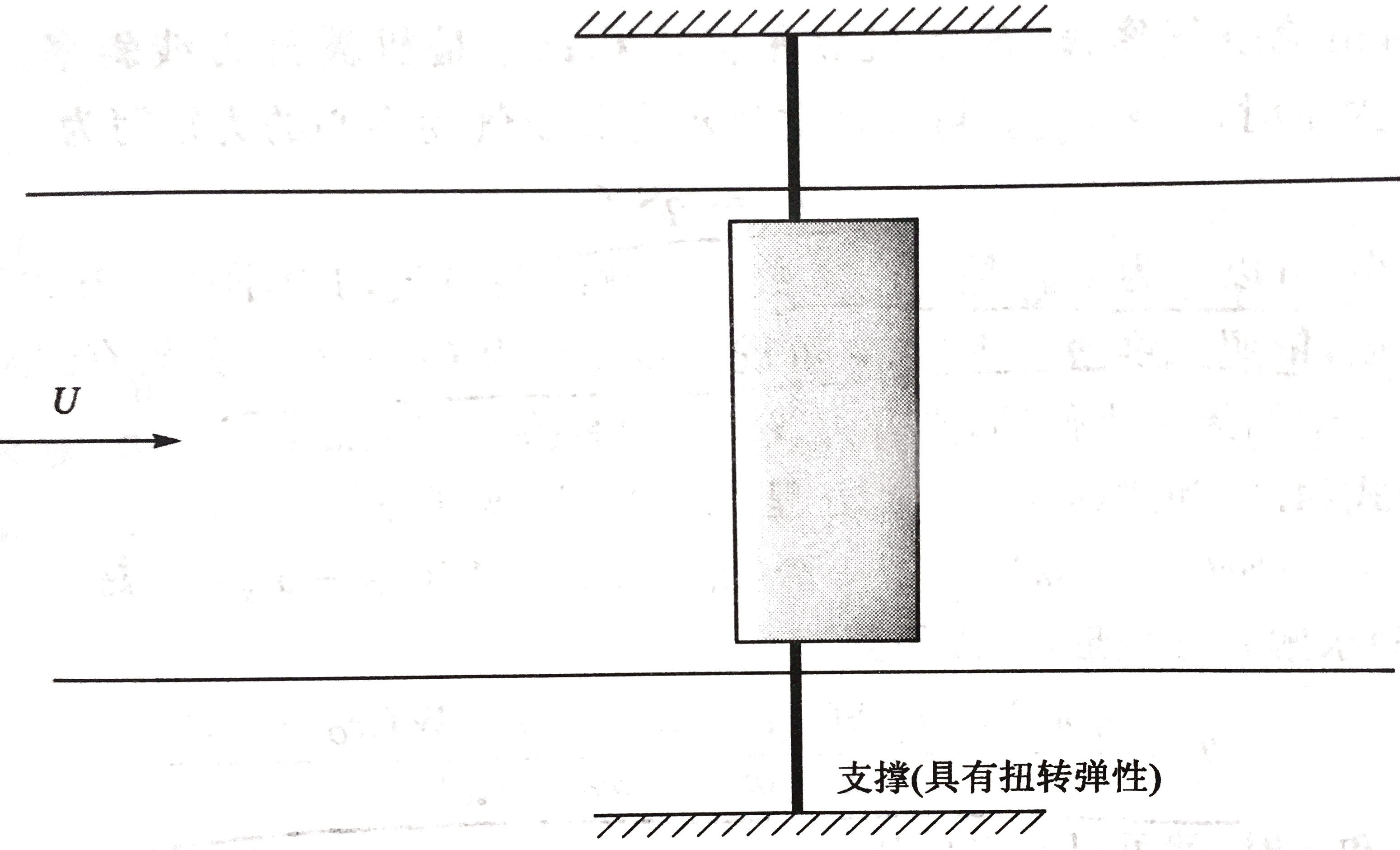
考虑一个刚硬的、展向均匀的机翼模型,安装在风洞侧壁上,可以绕支撑轴俯仰运动。扭转弹簧约束了机翼的俯仰运动。如图所示:
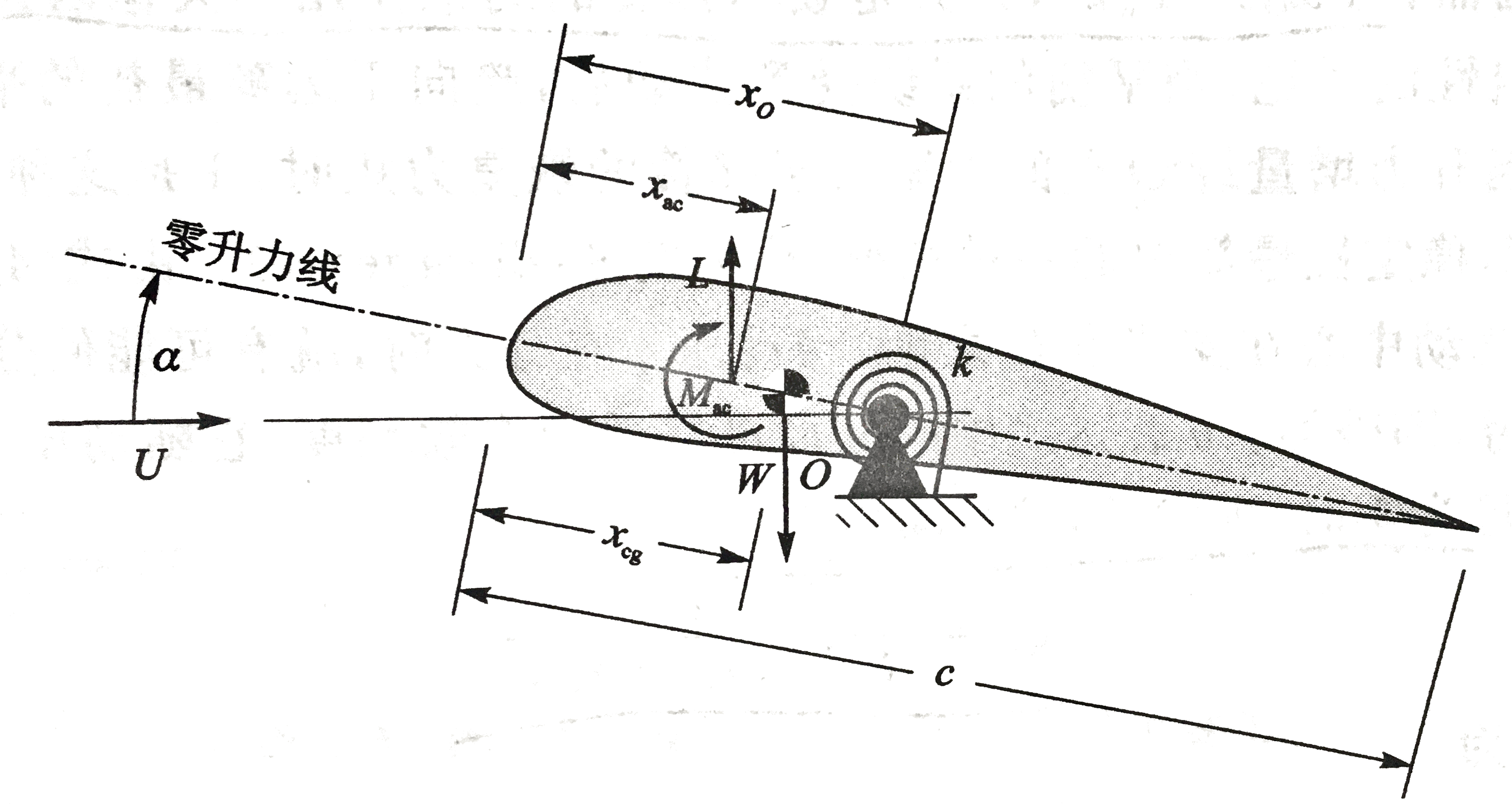
假设刚体安装转轴上的支撑点O(刚心)上,O点到前缘的距离为xO。支撑弹簧的扭转刚度为k。初始攻角为αr。焦心到前缘的距离为xac。重心到前缘的距离为xcg。弦长为c。俯仰角的扭转变形(弹簧扭转角)为θ。关于焦心的气动扭转力矩为Mac。升力为L。重力为W。自由气流速度为U。自由空气密度为ρ∞。则:
Mac+L(xo−xac)−W(xo−xcg)−kθ=0
按照线性空气动力学,升力为
L=qSCLα(αr+θ)
气动力矩为
Mac=qScCMac
q=21ρ∞U2为来流动压,CLα为升力线斜率,CMac为力矩系数,可以被认为常数。于是:
qScCMac+qSCLα(αr+θ)(xo−xac)−W(xo−xcg)=kθ
变形得:
θ=k−qSCLα(xO−xac)qScCMac+qSCLααr(xo−xac)−W(xo−xcg)(2.1.1)
上式分母为零时,θ无穷大,发生扭转破坏,即机翼发散。此时有
q=qD=SCLα(xO−xac)k(2.1.2)
qD为发散动压,代入动压表达式中得,发散速度为:
UD=ρ∞SCLα(xO−xac)2k
动压只能为有限正值,则当xO≤xac(刚心位于焦心之前)时,机翼不会发散。
为了简化公式,考虑翼型为对称机翼(CMac=0),且假设重心与刚心重合(xO=xcg),将(2.1.2)代入(2.1.1)得:
θ=qqD−1αr
取倒数:
θ1=αrqD(q1−qD1)
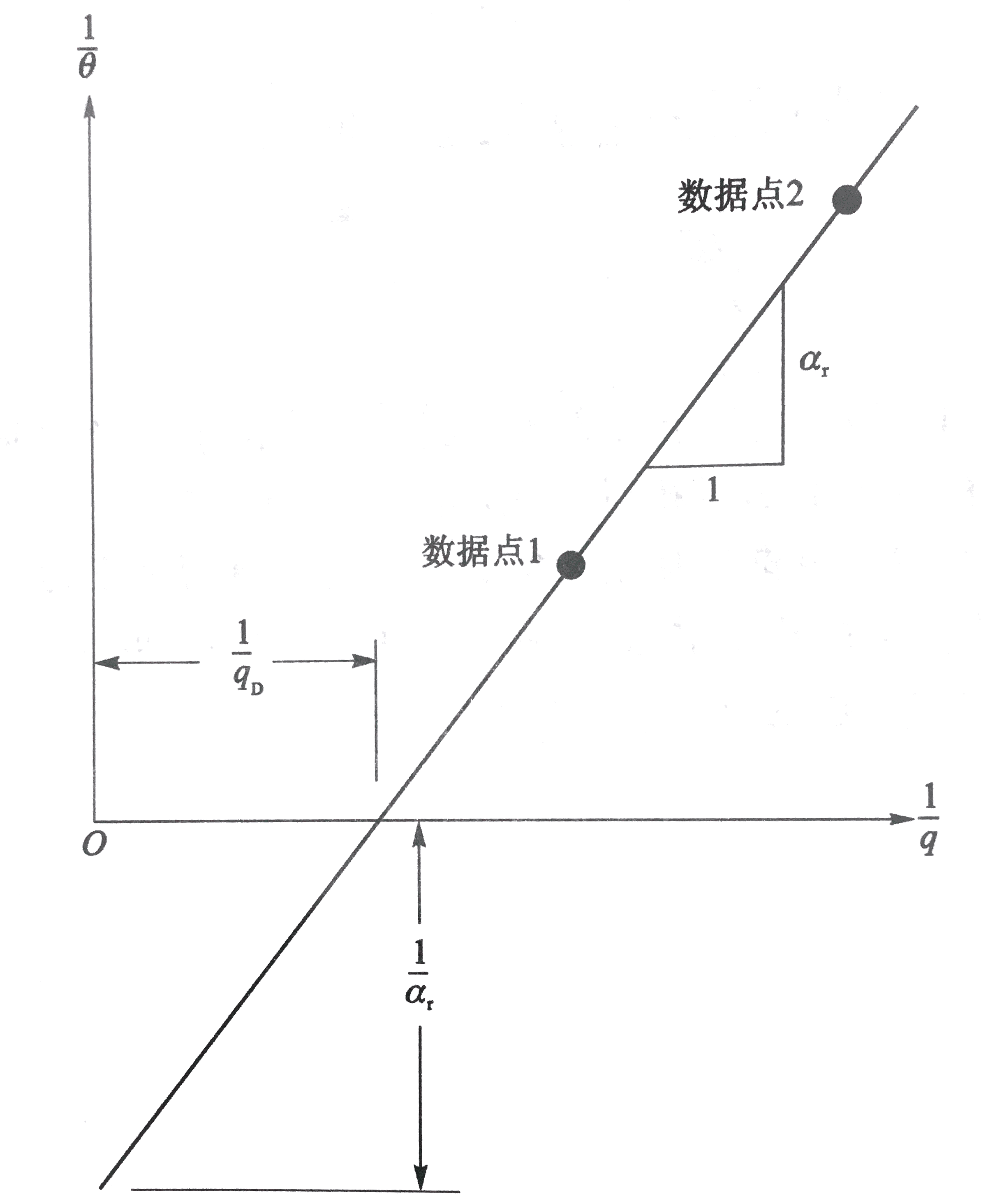
可以看出1/θ正比于1/q。于是可用两组动压-转角实验值估算出发散动压,如图所示:
2.2 应用于副翼反效的洞壁安装模型
副翼反效是指由于机翼结构变形导致副翼的预期相应反向。
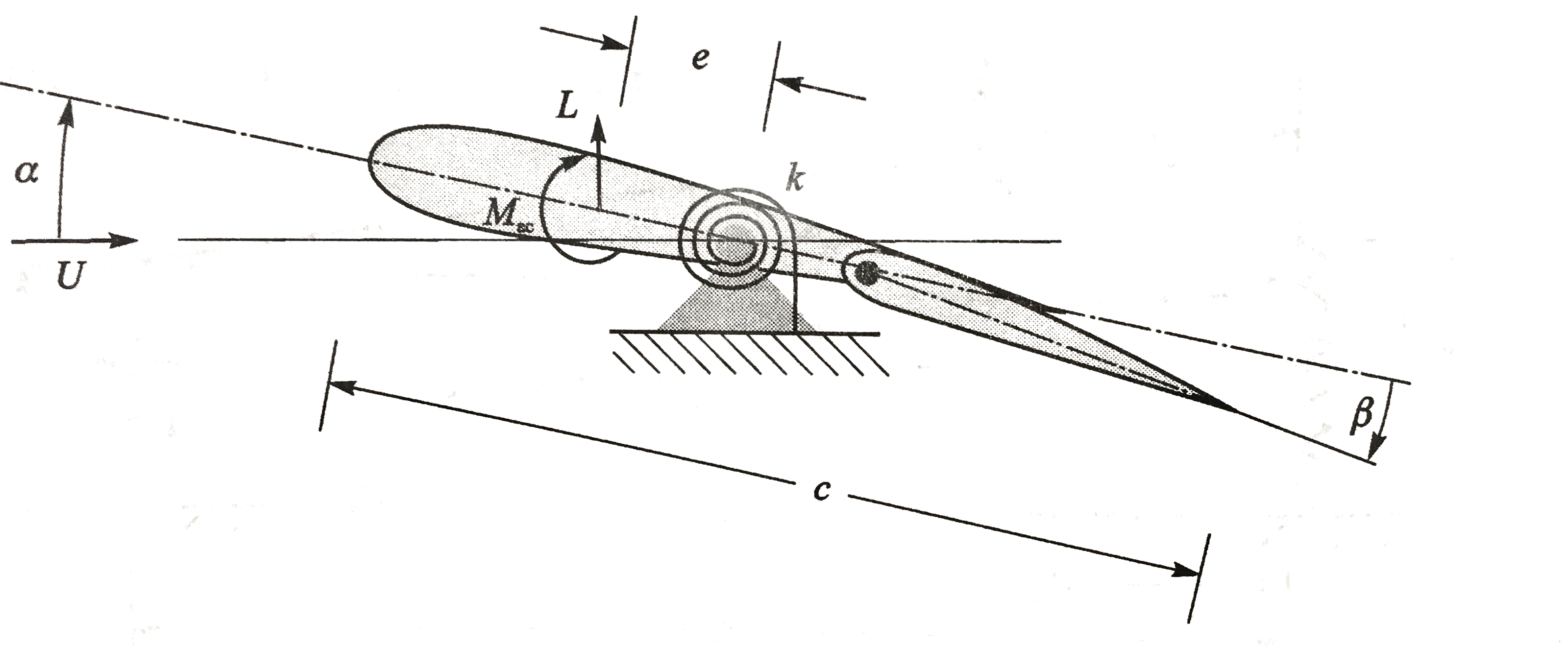
给出如图所示的二元机翼截面。其中后缘的副翼可以根据操纵系统的指令偏转任意角度β;这时不考虑重力。
绕转轴的力矩平衡方程为
Mac+eL=kθL=qSCLMac=qcSCMac
根据线性理论,α和β都是小量,故
CL=CLαα+CLββCMac=CM0+CMββ
其中:α=αr+θ,cMβ<0,假设为对称翼型(CM0=0)。
求得机翼扭转角公式:
θ=k−eqSCLαqS[eCLααr+(eClβ+cCMβ)β]
可得发散动压:
qD=eSCLαk(2.2.1)
可以看出发散动压不受副翼的影响。
根据上面求得的机翼扭转公式,反代入升力函数:
L=1−keqSCLαqS[CLααr+CLβ(1+kCLβcqSCLαCMβ)β](2.2.2)
注意cMβ<0。可以看出,β的系数中既有大于零的因素,又有小于零的因素。当动压q过大时会使β系数总体小于零。
令升力L对β的偏导为零:
∂β∂L=0=1−keqSCLαqSCLβ(1+kCLβcqSCLαCMβ)
得到反效动压:
qR=−cSCLαCMβkCLβ(2.2.3)
联立(2.2.1)(2.2.2)(2.2.3)得
L=1−qDqqS[CLααr+CLβ(1−qRq)β]
定义副翼的升力效率:
η=刚硬机翼单位副翼偏角引起的升力变化弹性机翼单位副翼偏角引起的升力变化=1−qDq1−qRq
3 均匀升力面
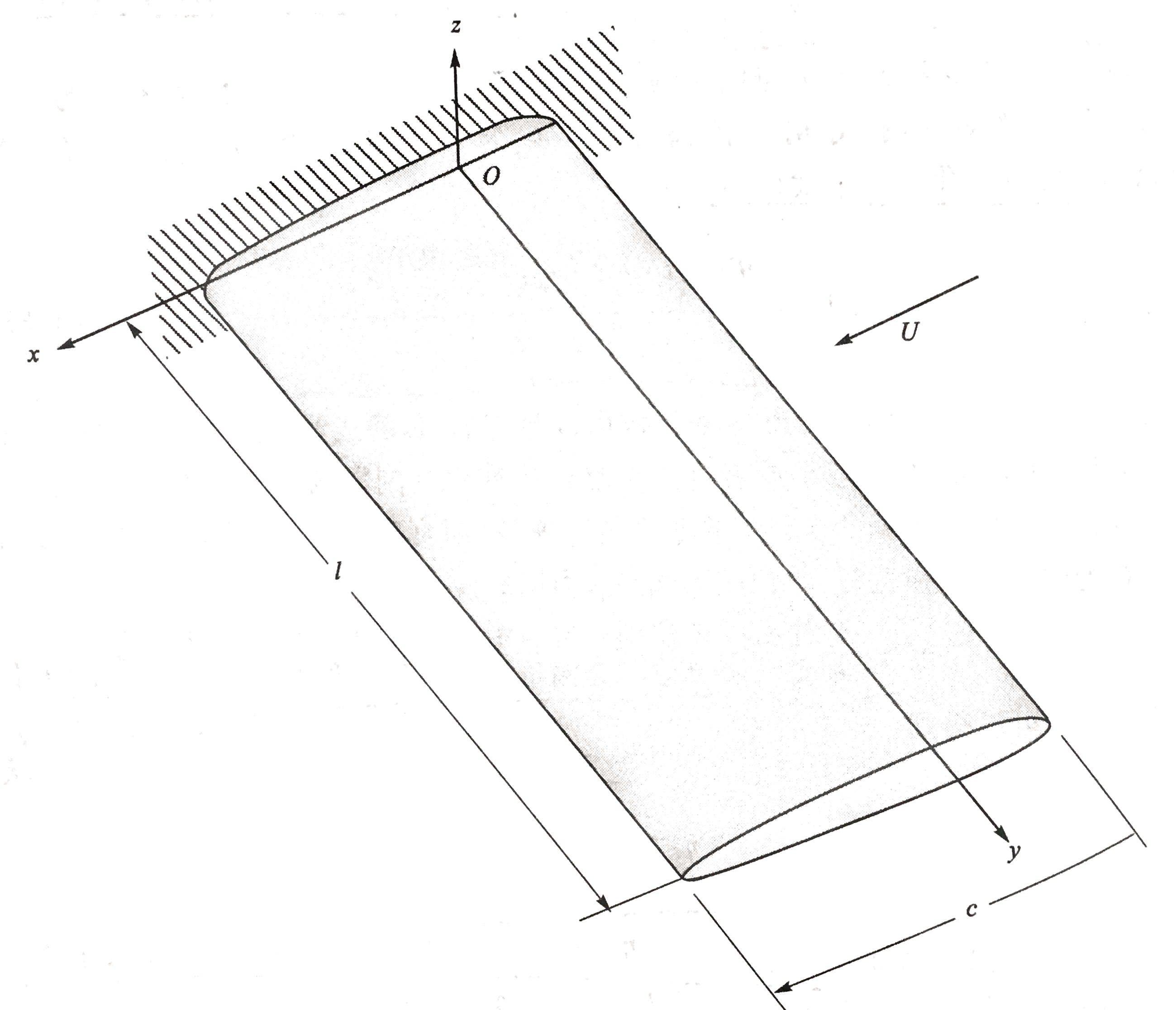
考虑一个无后掠均匀弹性升力面,如图所示,简化为梁模型,梁的根部固支,梢部自由。定义y轴为弹性轴(即为各剖面刚心的连线)。
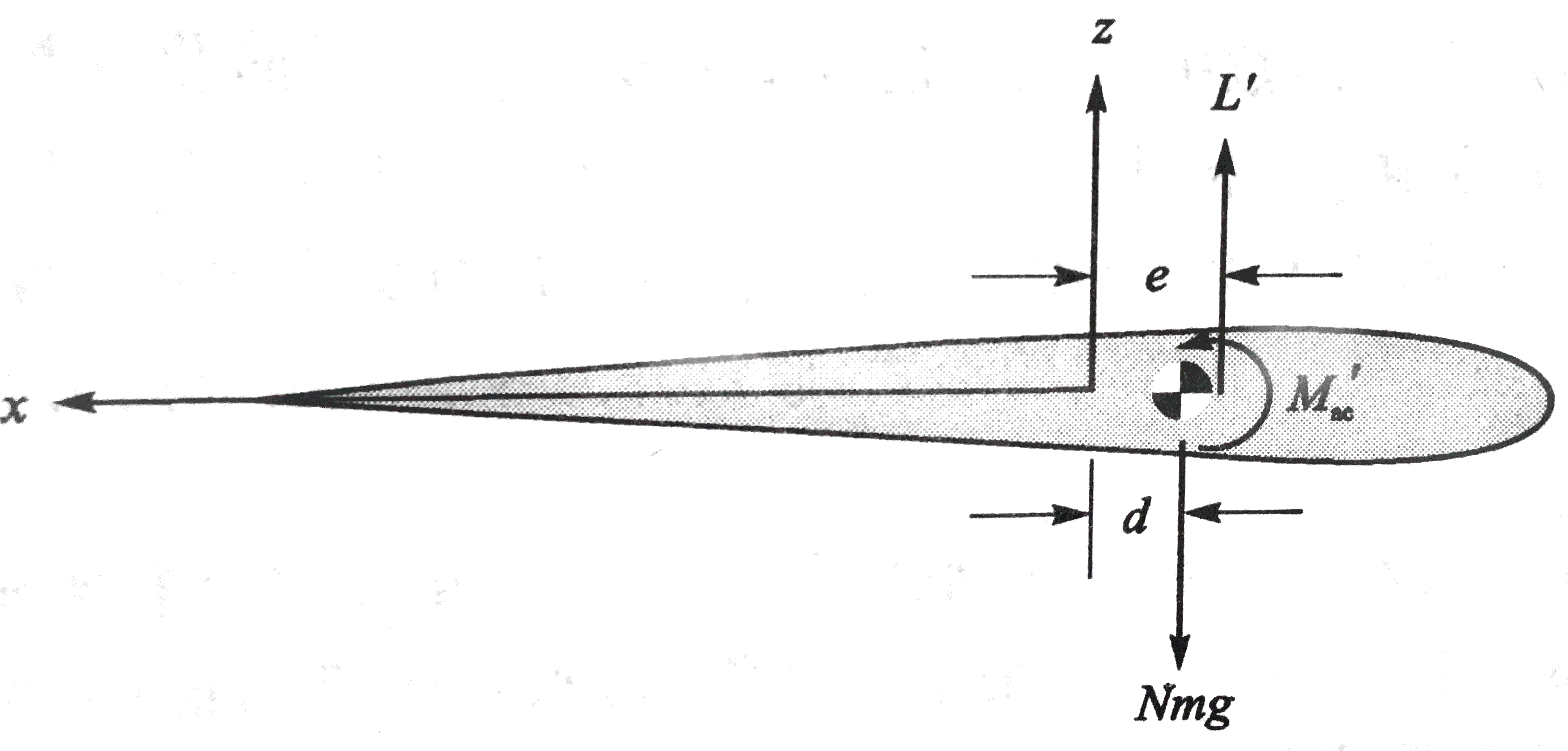
L′和Mac′为单位展长的升力和俯仰力矩,mg为单位展长的重力,N为z方向的过载。于是单位展长上总的外加分布扭矩:
M′=Mac′+eL′−Nmgd(3.0.1)
其中:
L′=qcclMac′=qc2cmac
q=21ρ∞U2为来流动压,cl为升力系数,cmac为力矩系数,可以被认为常数。
设扭转角为θ,刚性攻角为αr,升力线斜率为a,于是升力系数为
cl=a(αr+θ)
扭转变形的基本本构关系为:
T=GJdydθ
于是
−M′=dydT=dyd(GJdydθ)
将相关数据代入(3.0.1)得
dy2d2θ+GJqcaeθ=−GJ1(qc2cmac+qcaeαr−Nmgd)(3.0.2)
边界条件表示为:
y=0:θ=0y=l:dydθ=0}(3.0.3)
3.1 平直机翼扭转发散
记
λ2=GJqcaeαr=aeccmac−qcaeNmgd
于是(3.0.2)可写作
dy2d2θ+λ2θ=−λ2(αr+αr)(3.1.1)
解此微分方程并代入边界条件(3.0.3)得:
θ=(αr+αr)[tan(λl)sin(λy)+cos(λy)−1](3.1.2)
注意到当λl为π/2时,θ为无穷大,机翼发生扭转破坏,扭转发散。
代入λ2表达式中,对应动压为发散动压:
qD=ecaGJ(2lπ)2(3.1.3)
由于动压只能为有限正值,所以当弹性轴不位于焦心之后(e≤0)时,机翼不会发散。
3.2 平直机翼副翼反效
对于有副翼的机翼,副翼偏角为β。需要修正剖面升力系数和俯仰力矩系数:
cl=a(αr+θ)+clββcmac=cmββ
取αr=0,则剖面升力和俯仰力矩为
L′=qc(aθ+clββ)M′=eL′+qc2cmββ
于是(3.1.1)可修正为
dy2d2θ+λ2θ=−λ2ψβ(3.2.1)
其中
ψ=aeeclβ+ccmβλ2=GJqcae
解(3.2.1)并代入边界条件(3.0.3)得
θ=−ψβ[1−cos(λy)−sin(λy)tan(λl)](3.2.3)
可以看出发散动压和副翼无关。
则可以得到均匀升力面的总升力:
L=∫0lL′dy=eqcl[(eclβ+ccmβ)λltan(λl)−ccmβ]β
由L对β的偏导数等于零可得
λltan(λl)=ccmβ+eclβccmβ
上面方程的最小解为λ1l。于是反效动压为
qR=ecal2(λ1l)2GJ(3.2.4)
3.3 后掠效应
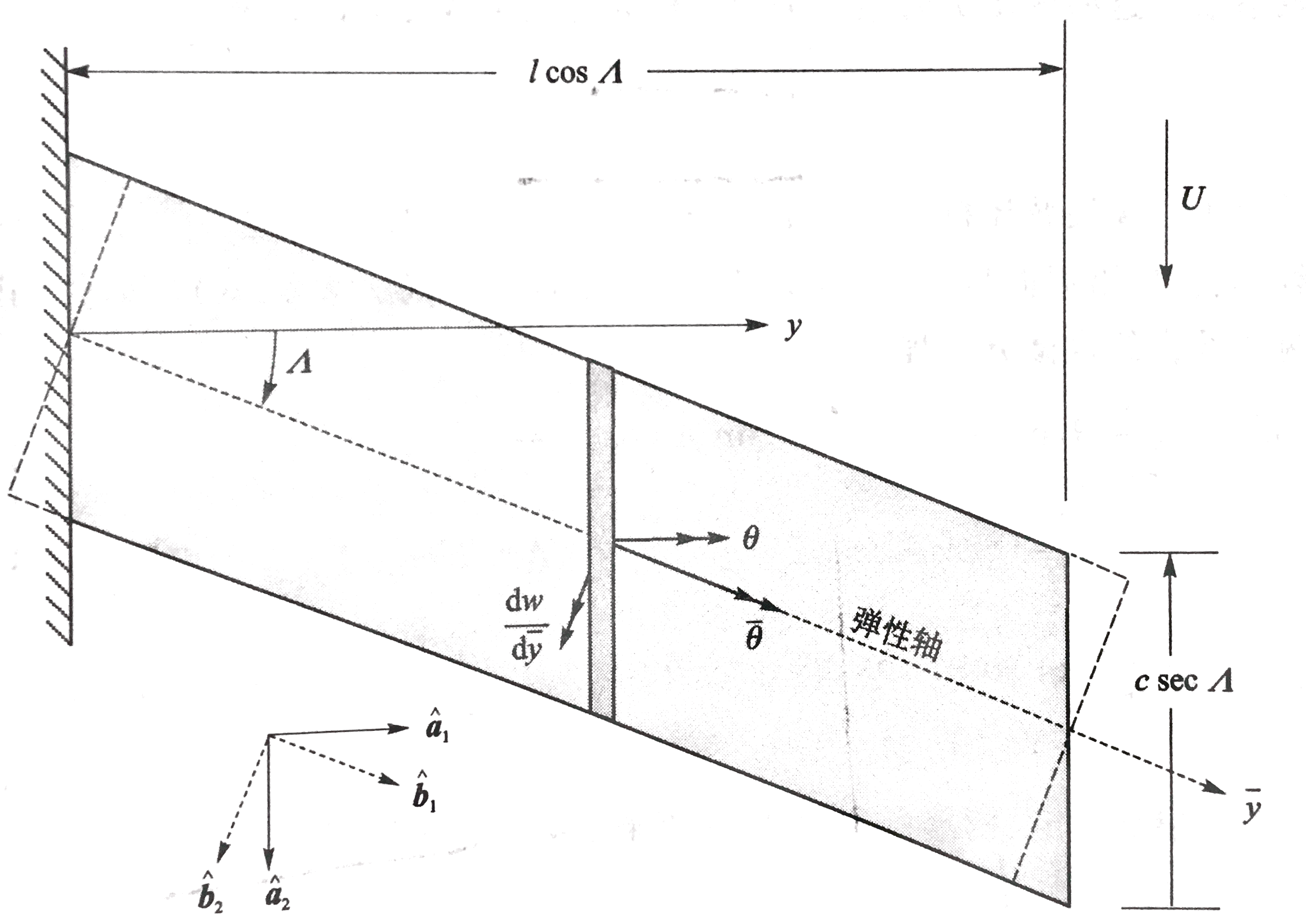
考虑机翼模型具有后掠角,如图所示。引入单位向量a1、a2分别沿y轴和来流方向。再引入一对单位向量b1、b2是a1、a2转动一个后掠角Λ得到的。
有几何关系:
b1=cosΛa1+sinΛa2b2=−sinΛa1+cosΛa2
此时弹性变形引起的剖面结构的总转动,可以表示为机翼扭转θ(b1向)引起的转动和机翼弯曲dw/dy(b2向)引起的转动之和:
θ=(θb1+dydwb2)⋅a1=θcosΛ−dydwsinΛ(3.3.1)
扭矩平衡方程和剪力平衡方程为
dyd(GJdydθ)=−qecaα−qc2cmac+Nmgddy2d2(EIdy2d2w)=qcaα−Nmg
其中α=αr+θ,a表示后掠机翼二维升力线斜率,cmac表示二维俯仰力矩系数:
a=acosΛcmac=cmaccos2Λ
于是:
θ′′+GJqecaθcos2Λ−GJqecaw′sinΛcosΛ=−GJ1(qecaαrcosΛ+qc2cmaccos2Λ−Nmgd)w(4)+EIqcaw′sinΛcosΛ−EIqcaθcos2Λ=EI1(qcaαrcosΛ−Nmg)⎭⎪⎪⎪⎪⎬⎪⎪⎪⎪⎫(3.3.2)
边界条件为
y=0:θ=0(零扭转)y=0:w=0(零弯曲挠度)y=0:w′=0(零弯曲转角)y=l:θ′=0(零扭矩)y=l:w′′=0(零弯矩)y=l:w′′′=0(零剪力)⎭⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎫(3.3.3)
若要求解发散动压,只需要考虑方程(3.3.2)的其次部分:
θ′′+GJqecaθcos2Λ−GJqecaw′sinΛcosΛ=0w(4)+EIqcaw′sinΛcosΛ−EIqcaθcos2Λ=0}
将上面第一个方程对y求导,在乘以cosΛ,得到的结果减去乘以了sinΛ的第二个方程,结合(3.3.1)得到
θ′′′+GJqecacos2Λθ′+EIqcasinΛcosΛθ=0
引入无量纲量η=y/l,用()′表示d()/dη:
θ′′′+GJqecal2cos2Λθ′+EIqcal3sinΛcosΛθ=0(3.3.4)
边界条件(3.3.3)可表示为
θ(0)=θ′(1)=θ′′(1)+GJqecal2cos2Λθ(1)=0(3.3.5)
Diederich和Budianshy获得方程(3.3.4)(3.3.5)的精确解(1948年),但相当复杂。下面用近似解代替解析解的一个分支,此分支恰好为物理角度最重要的分支。定义
τ=GJqecal2cos2Λβ=EIqcal3sinΛcosΛ}
根据Diederich和Budianshy的解,在发散边界处一定范围内,τ=τD和β=βD近似满足方程
τD=4π2+763π2βD(3.3.6)
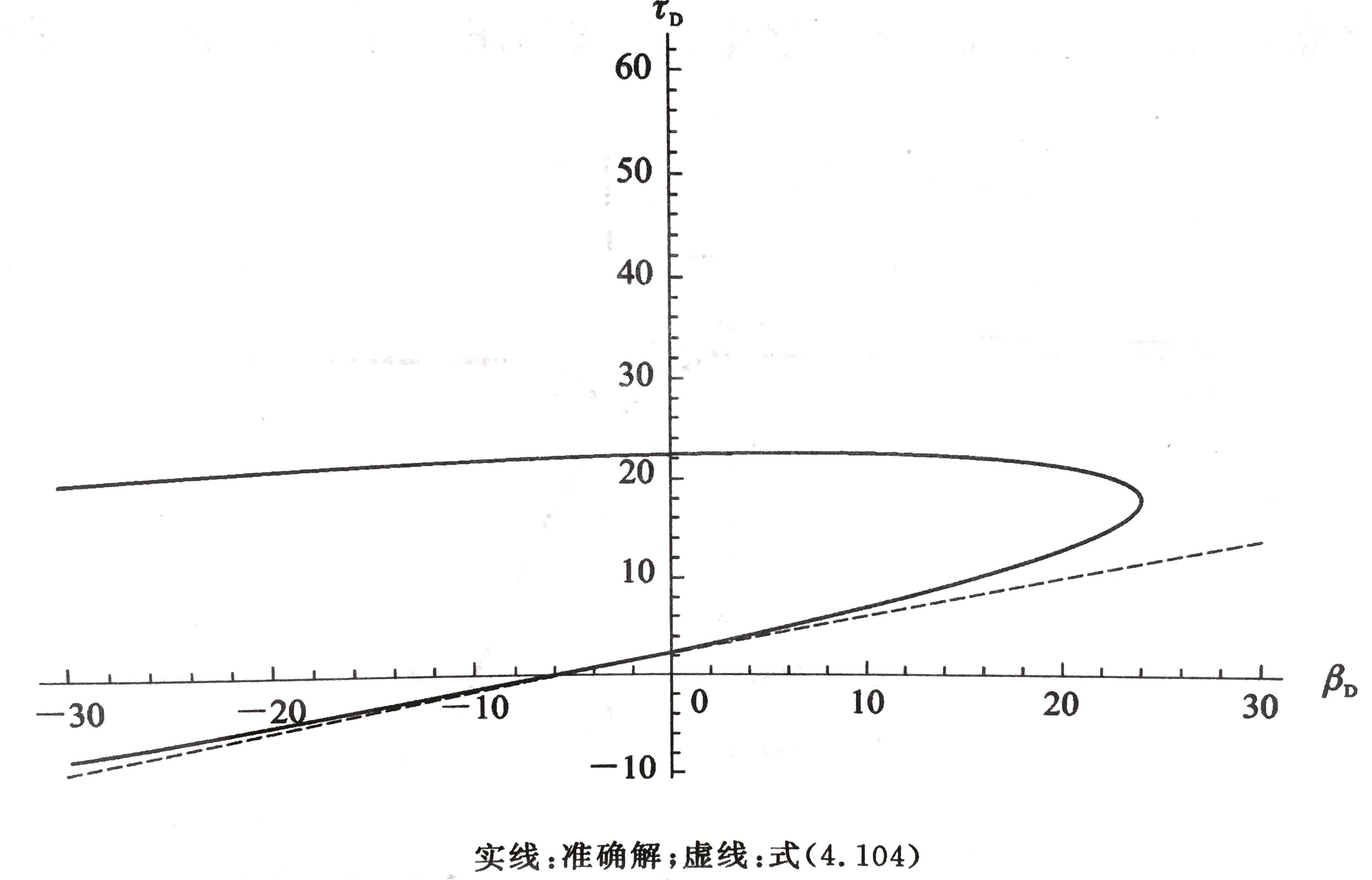
近似解和精确解的比较如图所示
可以看出在原点附近直线的近似解与精确解十分吻合。
引入无量纲参数r:
r=τβ=elEIGJtanΛ
于是(3.3.6)变为
τD=4π2+763π2rτD
进而解出:
τD=4(1−763π2r)π2
结合τ的定义式得发散动压:
qD=4ecal2cos2Λ(1−763π2elEIGJtanΛ)GJπ2
可以看出(3.1.3)为后掠角为零的动压,即
qD0=4ecal2π2GJ
于是
qD0qD=1−763π2elEIGJtanΛ1+tan2Λ
qD只能为有限正值,所以发散仅仅出现在∣Λ∣=90∘且763π2elEIGJtanΛ=1时。令
tanΛ∞=3π2GJl76EIe
则只有当−90∘<Λ<Λ∞时,会出现发散,且:
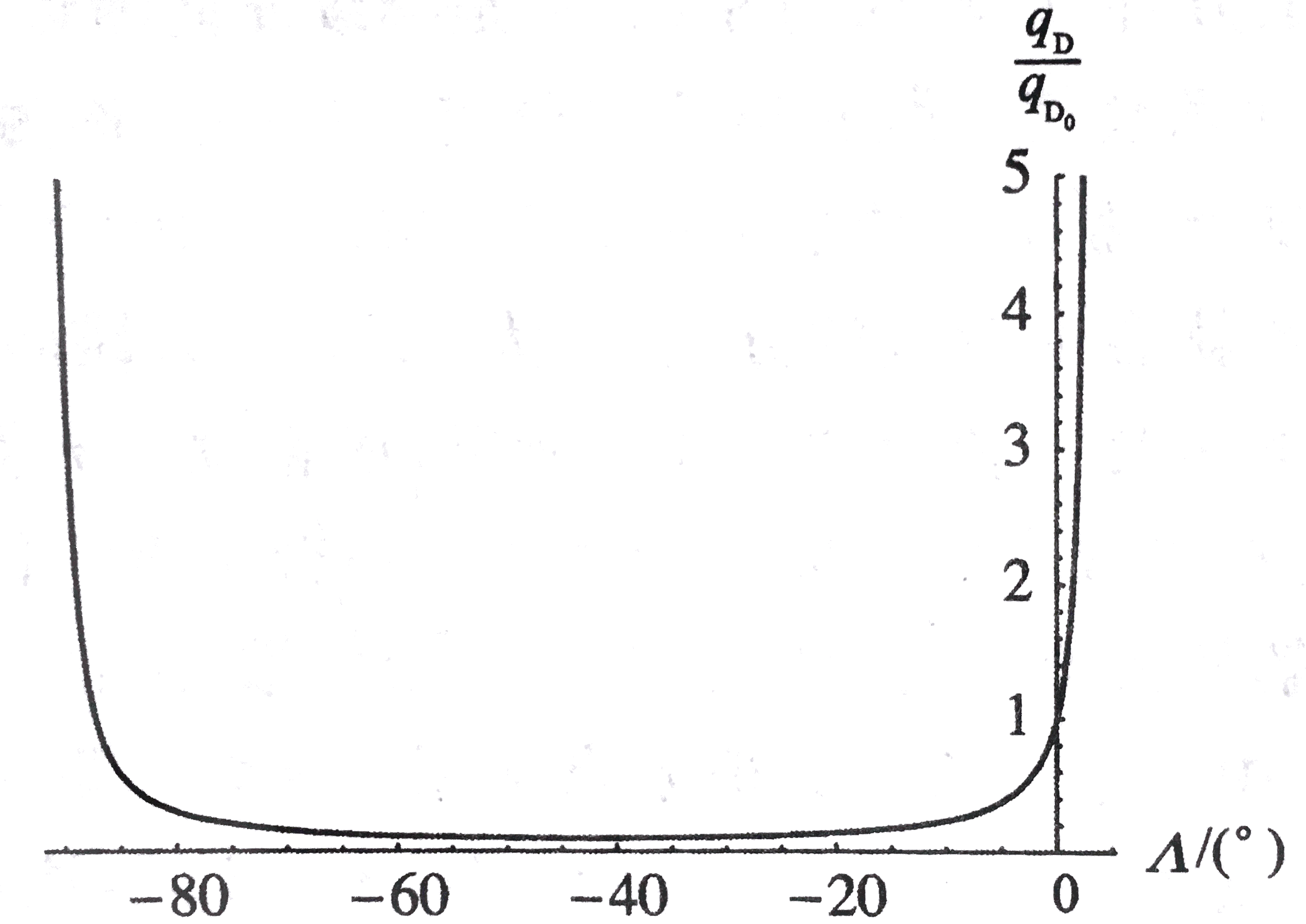
qD0qD=1−tanΛ∞tanΛ1+tan2Λ
其当Gj/EI=1.0、e/l=0.02时,函数图像如图所示
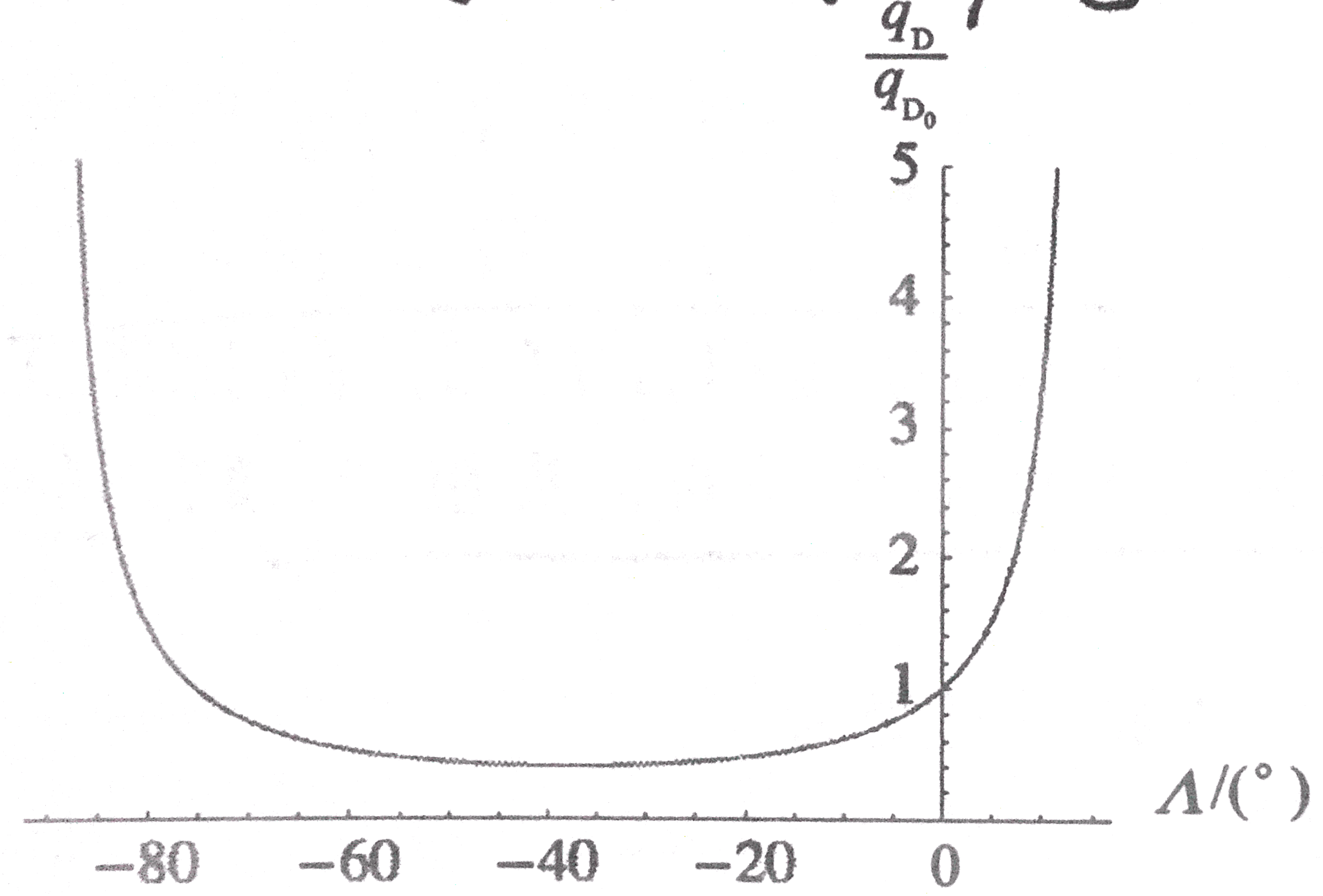
当时Gj/EI=0.2、e/l=0.02,函数图象如图所示
可以看出选择后掠角Λ≥Λ∞可避免机翼发散,但前掠翼飞机很容易在较小动压下机翼发散。
同时可以看出当扭转刚度与弯曲刚度比值减小时,其Λ∞增大,即需要增大后掠角以避免机翼发散。
3.4 复合材料机翼和气动剪裁
由前一节知,普通材料前掠发散速度过低。而使用复合材料则可以消除这一弱点。
复合材料的显著特点是各向异性,在不同方向上有不同的材料属性(如刚度)。且对于复合梁存在着扭转和弯曲的耦合:
[TM]=[GJ−K−KEI][θ′w′′]
此时平衡方程变为
(GJθ′−Kw′′)′=−qecaα−qc2cmac+Nmgd(EIw′′−Kθ′)′′=qcaα−Nmg}(3.4.1)
边界条件为:
y=0:θ=0(零扭转)y=0:w=0(零弯曲挠度)y=0:w′=0(零弯曲转角)y=l:T=0(零扭矩)y=l:M=0(零弯矩)y=l:M′=0(零剪力)⎭⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎫(3.4.2)
求解发散条件时,只需写出(3.4.1)齐次部分。注意α=αr+θ:
θ′′−GJKw′′+GJqecaθcosΛ=0w(4)−EIKθ′′′+EIqcaθcosΛ=0}
与3.3节同样的处理方式得:
θ′′′+EIGJ−K2EIGJGJqecal2cos2Λ(1−EIKtanΛ)θ′+EIGJ−K2EIGJEIqcal3sinΛcosΛ(1−GJKtanΛ1)θ=0(3.4.3)
其中()′表示d()/dη。
边界条件(3.4.2)表示为:
θ(0)=θ′(1)=θ′′(1)+EIGJ−K2EIGJGJqecal2cos2Λ(1−EIKtanΛ)θ(1)=0(3.4.4)
可以观察到(3.3.4)、(3.3.5)和(3.4.3)、(3.4.4)结构一致,则解的结构一致。同样有
τ=EIGJ−K2EIGJGJqecal2cos2Λ(1−EIKtanΛ)β=EIGJ−K2EIGJEIqcal3sinΛcosΛ(1−GJKtanΛ1)}τD=4π2+763π2βD
于是:
qD=4π2EIGJEIGJ−K2ecal2cos2ΛGJ⋅1−EIKtanΛ−763π2elEIGJ(tanΛ−GJK)1
引入无量纲参量:
κ=EIGJK
则发散动压为:
qD=4ecal2cosΛ[1−κEIGJtanΛ−763π2elEIGJ(tanΛ−κGJEI)]π2GJ(1−κ2)(3.4.5)
qD0为后掠角为零的发散动压。于是:
qD0qD=1−κEIGJtanΛ−763π2elEIGJ(tanΛ−κGJEI)(1−κ2)(1+tan2Λ)
当发散动压为无穷大时后掠角为:
tanΛ∞=763π2EIGJel+EIGJκ1+763π2EIGJelκ(3.4.6)
于是:
qD0qD=(1+763π2EIGJelκ)(1−tanΛ∞tanΛ)(1−κ2)(1+tan2Λ)(3.4.7)
同样,仅当−90∘<Λ<Λ∞时,会出现发散。由于存在附加设计参数κ,且Λ∞随κ的减小而减小。所以当选择合适的κ时,可以使复合材料机翼在前掠时任然避免发散。
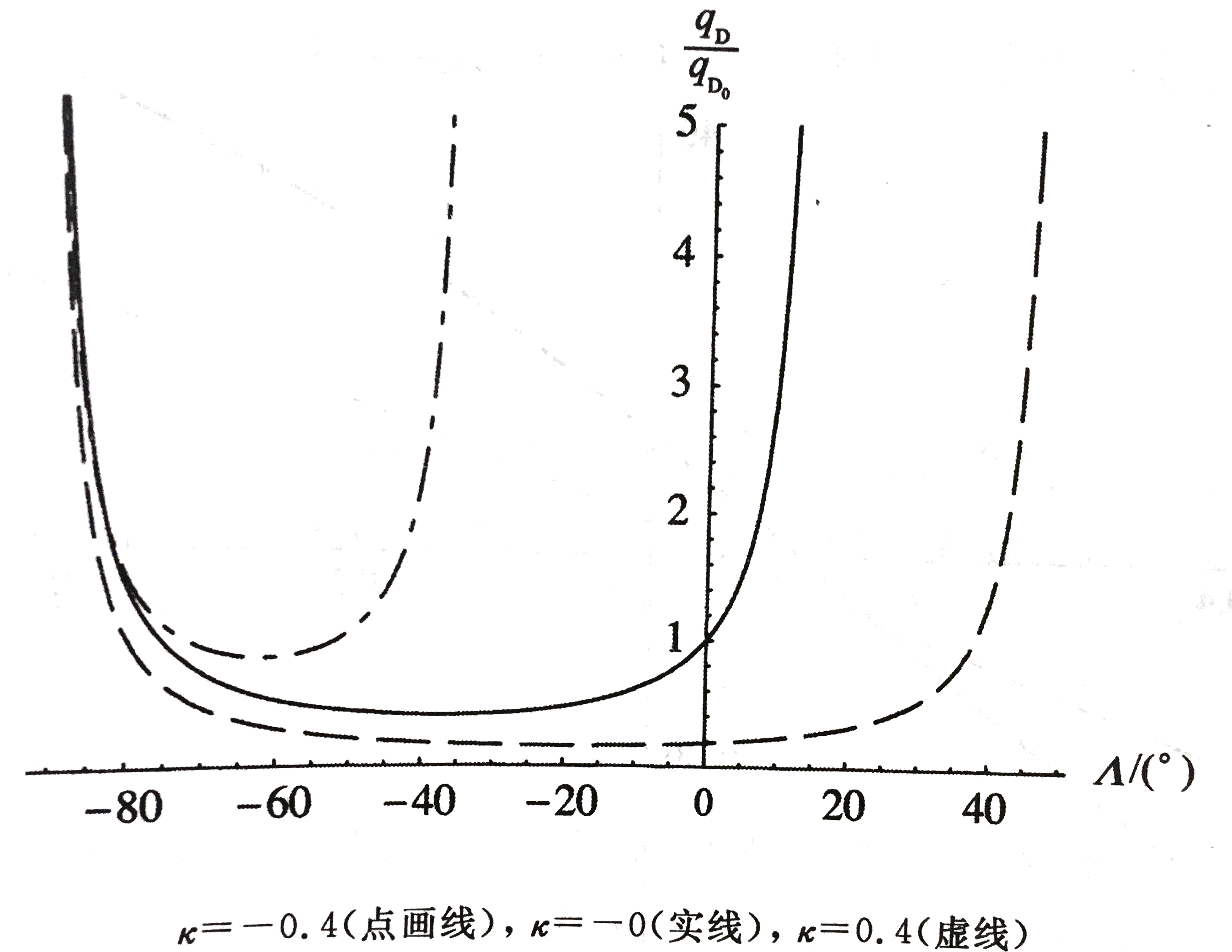
如图所示,GJ/EI=0.2且e/l=0.02时无量纲化的发散动压随后掠角变化曲线。
提升前掠机翼抗发散性能的方法有两个:减小扭转刚度和弯曲刚度比值;减小焦心刚心距和半展长的比值。
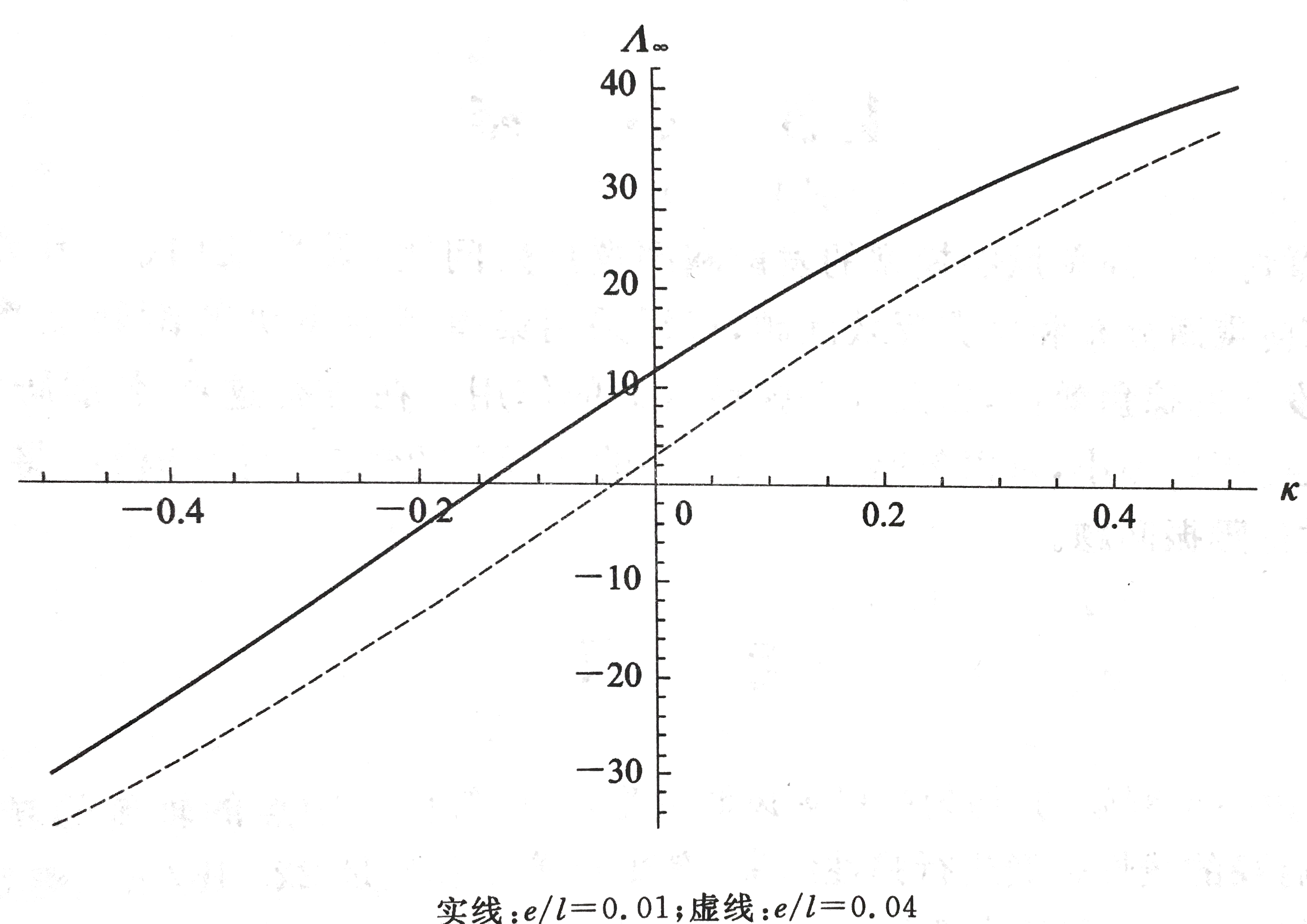
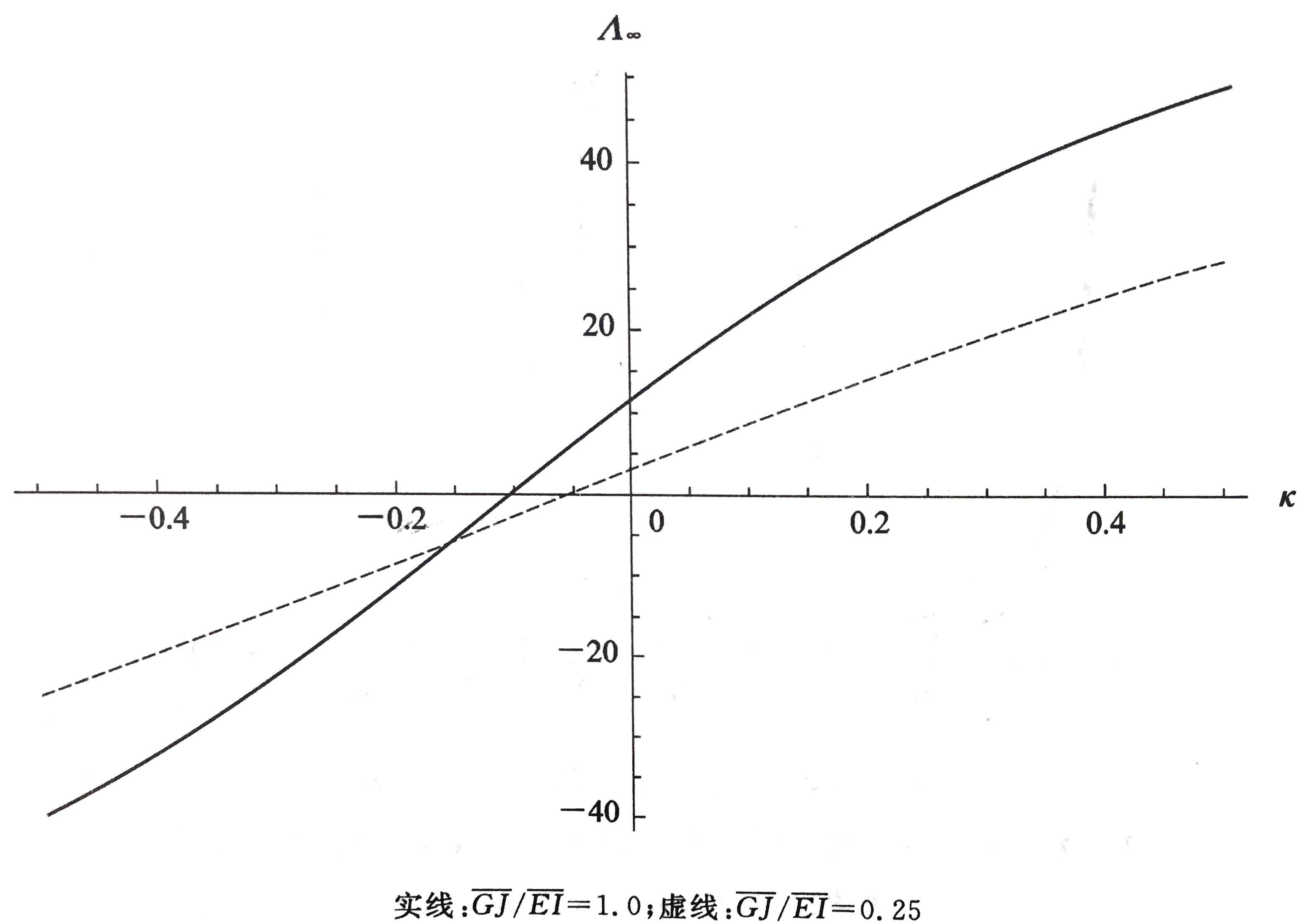
如图所示,e/l=0.02时,复合材料机翼无穷大发散动压后掠角随κ变化曲线。
如图所示,GJ/EI=0.5时,复合材料机翼无穷大发散动压后掠角随κ变化曲线。
4 总结
静气动弹性力学研究了机翼扭转发散、副翼反效以及后掠角(前掠角)效应。
本文章使用limfx的vsocde插件快速发布