气动弹性颤振涉猎
- 1 绪论
- 2 特征值分析的稳定性特征(p法)
- 3 典型翼段的气动弹性分析(p法-定常气动理论)
- 4 经典颤振分析(k法-无阻尼)
- 5 颤振问题的工程求解(k法、p-k法)
- 6 非定常气动力
- 7 根据假设模态进行颤振预测
- 8 颤振边界特性
- 9 总结
1 绪论
气动弹性颤振是飞行器结构在气动力、弹性力和惯性力三者共同作用下的一种动力学不稳定。颤振是自激振动且具有潜在破坏性的振动不稳定性,它是由在弹性物体上的气动力与它的固有振动模态耦合产生的,有增长振幅的振动运动。
涉及知识:空气动力学、结构动力学、理论力学、材料力学、高等数学、线性代数
2 特征值分析的稳定性特征(p法)
将升力面简化为板模型。令w(x,y,t)为在z向垂直于机翼平面(即x−y平面)的位移,ϕi(x,y)为固有振动模态,wi为对应的各阶固有频率,(ϕi(x,y)和wi只与模型的结构和边界条件有关,故视为已知量)则典型的结构位移可表示为
w(x,y,t)=i=1∑nξi(t)ϕi(x,y)
其中ξi(t)为第i阶模态的广义坐标。广义运动方程组:
Mi(ξ¨i+ωi2ξi)=Ξi(i=0,1,2,⋯,n)
其中Mi为广义质量,与质量分布m(x,y)相关,并确定为
Mi=∬planformm(x,y)ϕi2(x,y)dxdy
Ξi(t)为广义力,与外力载荷F(x,y,t)相关,并计算为
Ξi=∬planformF(x,y,t)ϕi(x,y)dxdy
外载荷只考虑气动载荷。压强分布Δp(x,y,t)可以用广义坐标及其导数的线性方程来表示:
Δp(x,y,t)=j=1∑n[aj(x,y)ξj(t)+bj(x,y)ξ˙j(t)+cj(x,y)ξ¨j(t)]+j=1∑Ndj(x,y)λj(t)
其中λj表示流场相关的状态变量。于是广义力表示为
Ξi(t)=∬planformΔp(x,y,t)ϕi(x,y)dxdy=j=1∑nξj(t)∬planformaj(x,y)ϕi(x,y)dxdy+j=1∑nξ˙j(t)∬planformbj(x,y)ϕi(x,y)dxdy+j=1∑nξ¨j(t)∬planformcj(x,y)ϕi(x,y)dxdy+j=1∑Nλj(t)∬planformdj(x,y)ϕi(x,y)dxdy=ρ∞b2U2[j=1∑n(aijξj+Ubbijξ˙j+U2b2cijξ¨j)+j=1∑Ndijλj]
其中
ρ∞b2U2aij=∬planformaj(x,y)ϕi(x,y)dxdyρ∞bUbij=∬planformbj(x,y)ϕi(x,y)dxdyρ∞cij=∬planformcj(x,y)ϕi(x,y)dxdyρ∞b2U2dij=∬planformdj(x,y)ϕi(x,y)dxdy
将相关量代入广义运动方程:
U2b2(Miξ¨i+Miωi2ξ)−ρ∞U2b2j=1∑ncijξ¨j−ρ∞Ubj=1∑nbijξ˙j−ρ∞j=1∑naijξj−ρ∞j=1∑ndijλj=0(i=1,2,⋯,n)(2.1)
同时由空气动力学理论可以得到N个附加方程:
j=1∑NAijλ˙j+bU(λi−j=1∑nEijξj)=0(i=1,2,⋯,N)(2.2)
由(2.1)和(2.2)联立,构成包含了n+N个方程的齐次线性常微分方程组,其中有n+N个未知函数。于是解的形式可以取作:
ξi(t)=ξiexp(vt),λi(t)=λiexp(vt)
代入方程(2.1)和(2.2)中,得到关于ξi和λi的n+N阶线性齐次代数方程组,矩阵形式为
[p2diag(M)+U2b2diag(Mω2)]ξ−ρ∞(p2c+pb+a)ξ−ρ∞dλ=0−Eξ+(pA+I)λ=0⎭⎪⎬⎪⎫(2.3)
其中p=bv/U为未知无量纲特征值,I为单位矩阵。
要求解广义坐标振幅的非平凡解,系数ξi和λi构成的行列式必须为0。即:
∣∣∣∣∣p2diag(M)+U2b2diag(Mω2)−ρ∞(p2c+pb+a)−Eρ∞dpA+I∣∣∣∣∣=0(2.4)
显然这个行列式是关于p的2n+N阶多项式。于是得到2n+N个根,包括nc对共轭复根和nr个实数根(2nc+nr=2n+N)。根的典型形式写作
vk=bUpk=Γk±iΩk(k=0,1,⋯,nc,⋯,nc+nr)(2.5)
其中,当nc≤k≤nc+nr时,Ωk=0。
将每一个pk代入(2.3)可以解得对应n维列阵ξ(k)(i=0,1,⋯,n)和N维列阵λ(k)(i=0,1,⋯,N)
于是位移场的解为
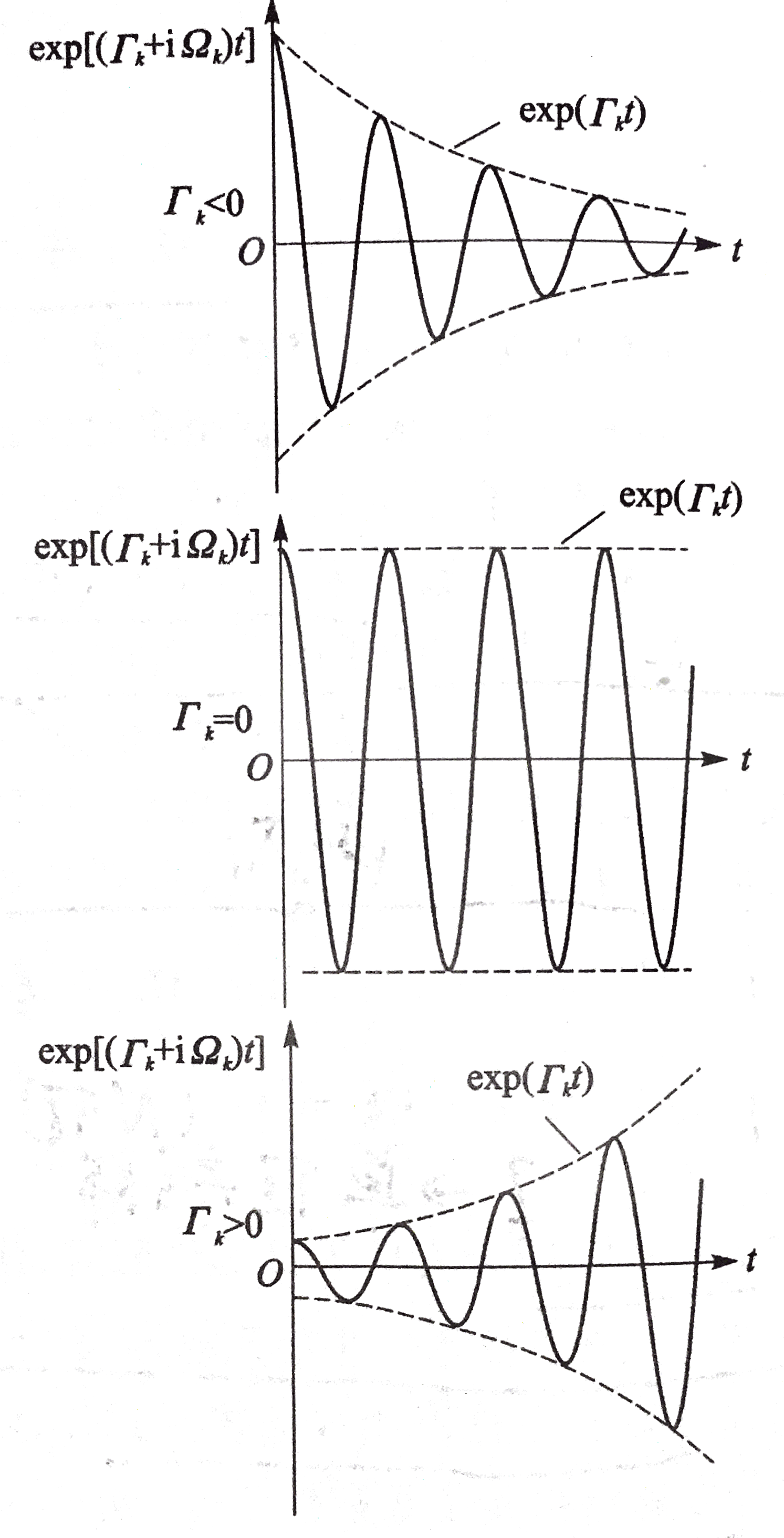
w(x,y,t)=k=1∑nc+nr{wk(x,y)exp[(Γk+iΩk)t]+wk(x,y)exp[(Γk+iΩk)t]}wk(x,y)=k=1∑nξi(k)ϕi(x,y)(k=1,2,⋯,nc+nr)(2.6)
wk为wk的共轭复数。
当Ω=0时各典型模态幅值的状态如图
则可以得出结论Γk和Ωk不同组合对应的运动状态类型和稳定特性:
| Γk | Ωk | 运动类型 | 稳定特征 |
|---|---|---|---|
| <0 | =0 | 衰减运动 | 稳定 |
| =0 | =0 | 简谐运动 | 临界稳定 |
| >0 | =0 | 发散运动 | 不稳定 |
| <0 | =0 | 收敛 | 稳定 |
| =0 | =0 | 与时间相关 | 临界稳定 |
| >0 | =0 | 发散 | 不稳定 |
可知,要求临界颤振条件只需要令Γk=0即可。
−Γk称为第k阶模态的模态阻尼,Ωk称为k阶模态的模态频率。
3 典型翼段的气动弹性分析(p法-定常气动理论)
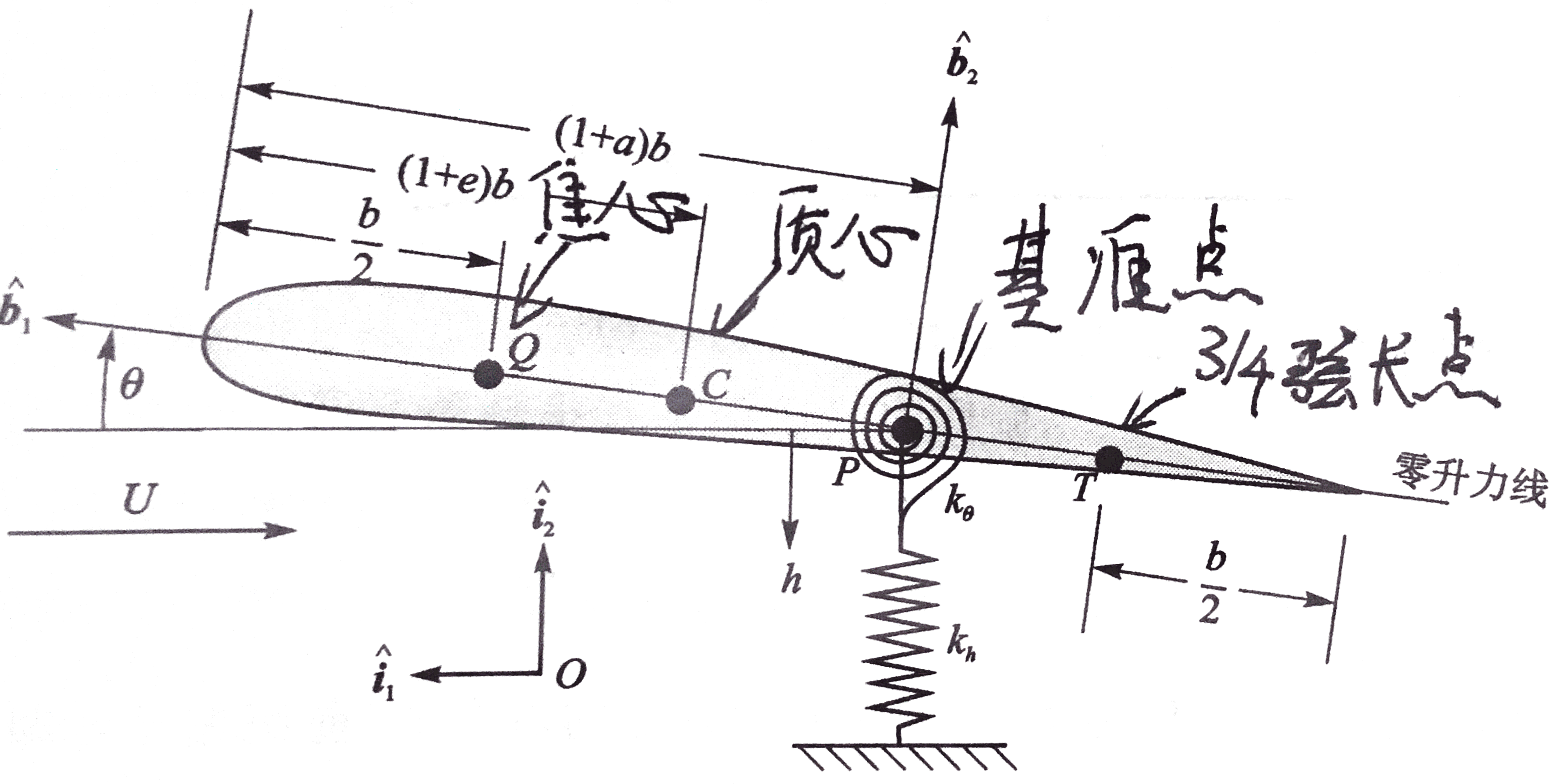
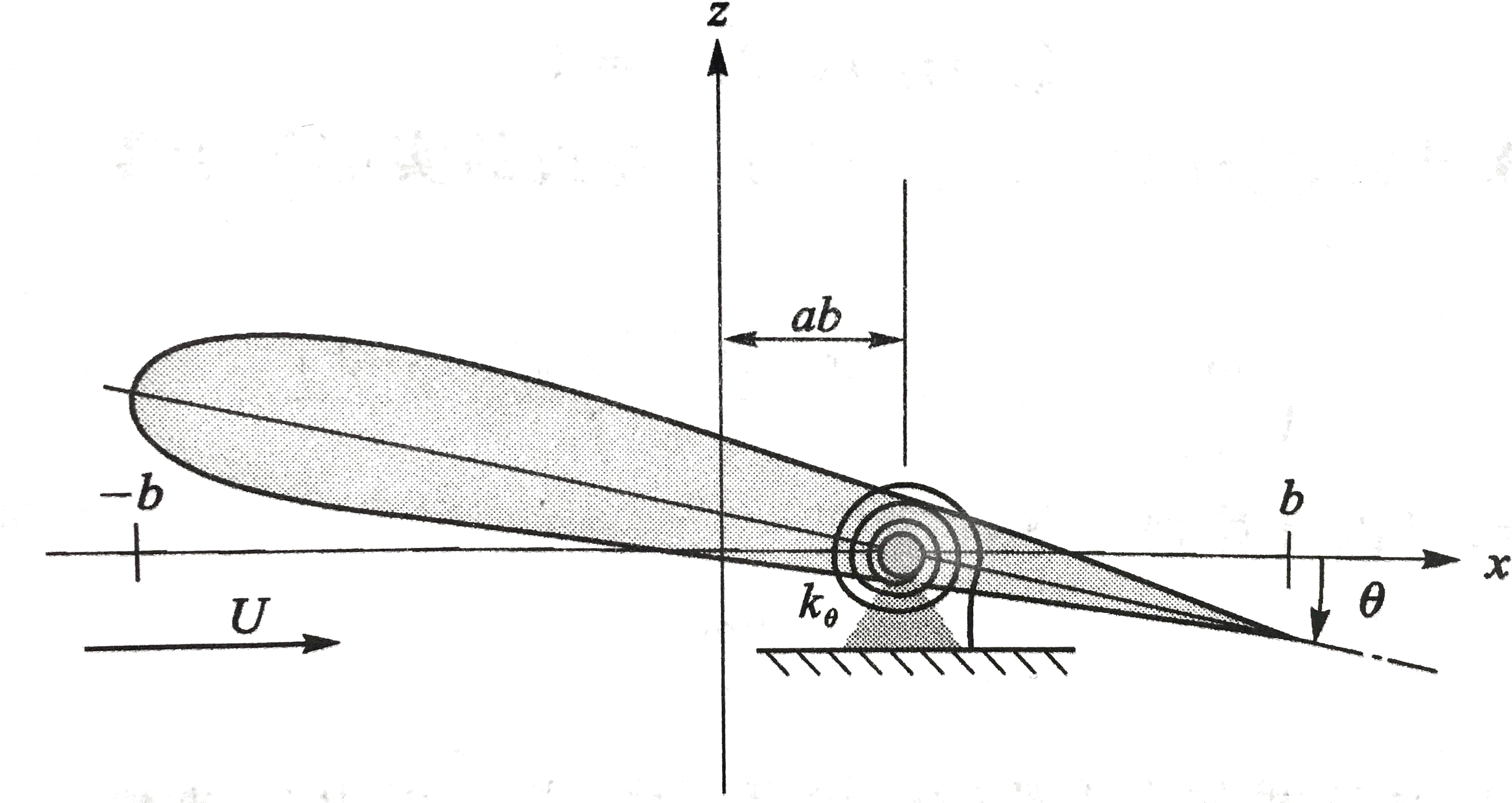
建立如图简单的、弹簧支承的刚硬机翼模型
该模型所关注的是P、C、Q和T,它们分别是参考基准点(即沉浮位移h的测量点),机翼质心、焦心(亚声速薄翼理论中假定为1/4弦长点)和3/4弦长点(薄翼理论中的一个重要弦向位置)。无量纲参数e、a(−1≤e≤1、−1≤a≤1)决定了C、P的位置。b为翼型半弦长。记xθ=e−a为静不稳定参数。模型的刚体沉浮、俯仰运动由线性轻质弹簧约束,弹簧常数分别为kh和kθ。
系统势能(不考虑重力势能)为
P=21khh2+21kθθ2(3.1)
质心C的速度为
vC=vP+θ˙b3×b[(1+a)−(1+e)]b1
其中,参考点P的惯性速度为
vP=−h˙i2
则:
vC=−h˙i2−bxθθ˙b2
动能为
K=21mvC⋅vC+21ICθ˙2
假设θ为小量,得
K=21m(h˙2+b2xθ2θ˙2+2bxθh˙θ˙)+21ICθ˙2=21m(h˙2+2bxθh˙θ˙)+21IPθ˙2(3.2)
Q点的虚位移为
δpQ=−δhi2+bδθ(21+a)b2
机翼的虚拟转角为δθb3
于是虚功为
δW=L[−δh+b(21+a)δθ]+M41δθ
因此广义力为
Qh=−LQθ=M41+b(21+a)L}(3.3)
将(3.1)、(3.2)、(3.3)代入拉格朗日方程中得
m(h¨+bxθθ¨)+khh=−LIPθ¨+mbxθh¨+kθθ=M41+b(21+a)L}(3.4)
这里采用定常气动理论和薄翼理论:
L=2πρ∞bU2θM41=0}
引入零空速时的非耦合结构固有频率:
ωh=mkh,ωθ=mkθ
将相关量代入(3.4),写作矩阵形式:
[mb2mb2xθmb2xθIP][bh¨θ¨]+[mb2ωh202πρ∞b2U2IPωθ2−2(21+a)πρ∞b2U2][bhθ]=[00]
设此齐次线性常微分方程组的解结构为h=hexp(vt)和θ=θexp(vt),并设v=Γ±iΩ。得到
[mb2v2+mb2ωh2mb2v2xθmb2v2xθ+2πρ∞b2U2IPωθ2θ+IPv2−2(a+21)πρ∞b2U2][bhθ]=[00]
引入无量纲参数:
p=Uvb,r2=mb2IP,σ=ωθωh,μ=ρ∞πb2m,V=bωθU
其中p和V是未知的无量纲复特征值。V表示无量纲空气的来流速度,也称为“减缩速度”。于是:
[p2+V2σ2xθp2xθp2+μ2r2p2+V2r2−μ2(a+21)][bhθ]=[00](3.5)
若存在非平凡解,则系数矩阵的行列式必须等于零:
∣∣∣∣∣∣p2+V2σ2xθp2xθp2+μ2r2p2+V2r2−μ2(a+21)∣∣∣∣∣∣=0(3.6)
从而得到关于p和V的方程。
将V视为函数自变量,p视为函数因变量。上面方程可以得到两组p的共轭复根:
p1=Ubv1=Ub(Γ1±iΩ1)=p1(V)p2=Ubv2=Ub(Γ2±iΩ2)=p2(V)}
它们分别对应俯仰(θ)频率和沉浮(h)频率。
乘以减缩速度V得
Vp1=Ub(Γ1±iΩ1)bωθU=ωθΓ1±iωθΩ1Vp2=Ub(Γ2±iΩ2)bωθU=ωθΓ2±iωθΩ2}
由第2节的结论知,当Γ=0Ω=0即p=0时,其对应的V=VD=UD/(bωθ)为发散速度的减缩速度。UD是发散速度。将p=0代入(3.6)式得:
VD=bωθUD=r1+2aμ
同样由第2节的结论知,当Γ=0Ω=0时,其对应的V=VF=UF/(bωθ)为颤振速度的减缩速度。UF是颤振速度。
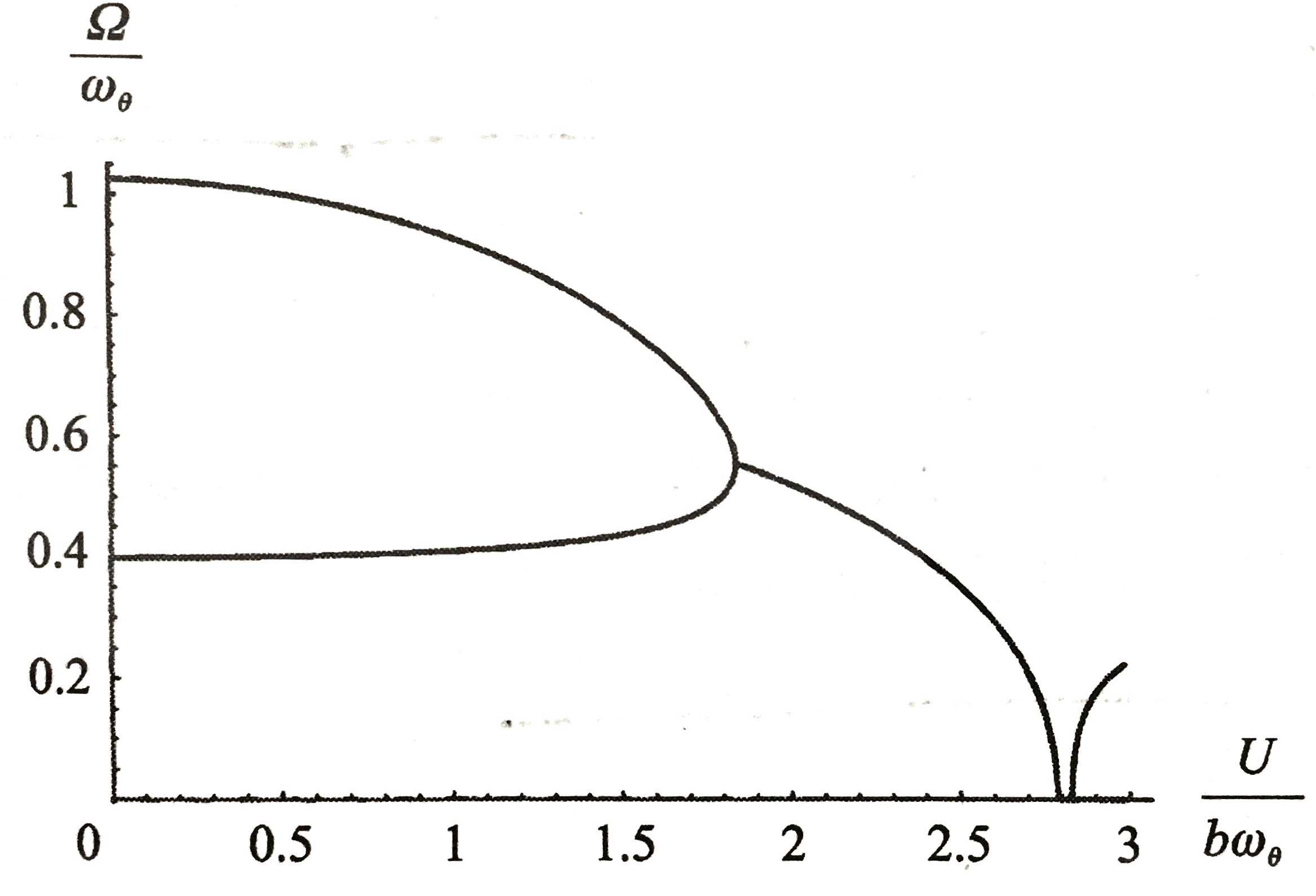
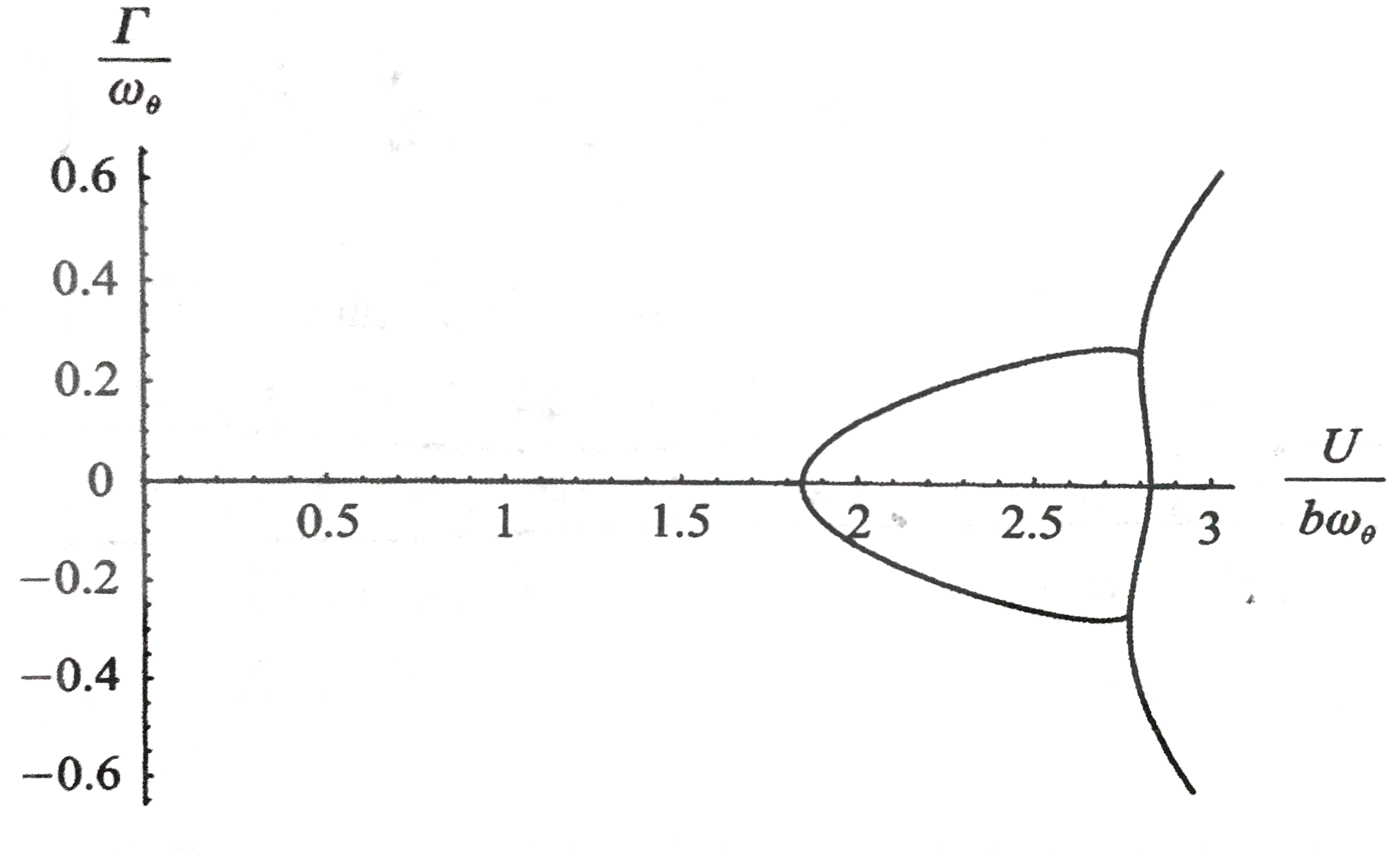
当a=−1/5e=−1/10μ=20r2=6/25σ=2/5时,方程(3.6)对应的V-p函数图像如图所示:
可以看出无量纲颤振速度为VF=UF/(bωθ)=1.843,颤振频率为ΩF/ωθ=0.5568。
此外,当V逼近VF时俯仰与沉浮频率靠近。这条性质在颤振分析中常作为判断依据。
然而仅凭上述分析无法准确得出颤振速度,而且在低于颤振速度时,模态阻尼Γ=0不符合实际情况。同时,在颤振点上的两个根完全相等使得定常理论呈现出重合的特征。这与实验和观测均不相符合。
出现这些缺陷的原因在于使用了定常气动理论。然而非定常气动理论加入将会使得问题变为复杂。但如果预先假设运动为简谐运动,问题则可以大大简化。
4 经典颤振分析(k法-无阻尼)
根据第2节的结论知颤振边界对应的条件为:具有一个依赖于时间的简谐运动的模态。即某一阶的模态阻尼Γk=0。于是在求颤振边界时,可以设第3节的模型中:
h(t)=hexp(iωt)θ(t)=θexp(iωt)
即,运动为简谐运动。
因为这种简谐运动的振幅比较小,于是采用线性的空气动力学理论(非定常气动理论),所以得到的升力L和绕P点的俯仰力矩M也是简谐的:
L(t)=Lexp(iωt)M(t)=Mexp(iωt)
其中,气动载荷的振幅可以按照运动振幅的复线性函数计算得:
L=−πρ∞b3ω2[lh(k,Ma∞)bh+lθ(k,Ma∞)θ]M=πρ∞b4ω2[mh(k,Ma∞)bh+mθ(k,Ma∞)θ]
其中,lh,lθ,mh,mθ四个复数函数表示由沉浮运动和俯仰运动引起的无量纲气动升力系数和力矩系数。这些系数通常是参数k和Ma∞的函数。且
k=Ubω(减缩频率)Ma∞=c∞U(来流马赫数)
4.1 单自由度颤振
考虑一个单自由度气动弹性系统,由刚硬的二维机翼组成,允许它绕指定的参考点俯仰运动。如图所示:
根据前面的分析:
θ=θexp(iωt)M=Mexp(iωt)M=πρ∞b4ω2mθ(k,Ma∞)θ
系统的运动方程可以写作:
IPθ¨+kθθ=M
代入相关值:
kθ−ω2IP=πρ∞b4ω2mθ(k,Ma∞)
引入系统固有频率:
ωθ=IPkθ
可以得到颤振边界飞行条件的最终方程:
πρ∞b4IP[1−(ωωθ)2]+mθ(k,Ma∞)=0(4.1.1)
上述方程中mθ(k,Ma∞)为复数,所以可以写作:
πρ∞b4IP[1−(ωωθ)2]+ℜ[mθ(k,Ma∞)]+iℑ[mθ(k,Ma∞)]=0(4.1.2)
上述方程中有未知参数ω、ρ∞、k和Ma∞,考察四个变量的相互关系,看出有ω、ρ∞、U和c∞四个独立变量。而方程有实部和虚部对应相等两个关系。于是只要给定其中两个量,其他的量也可以求出。
下面介绍计算方法:
首先给定高度,确定来流空气密度ρ∞。将来流马赫数Ma∞暂定为零(即假设来流声速c∞相对于空速U极大,设为不可压缩流)。代入(4.1.2)中:
πρ∞b4IP[1−(ωωθ)2]+ℜ[mθ(k,0)]+iℑ[mθ(k,0)]=0
因此可以得到左边虚部为零,实部为零,即
ℑ[mθ(kF,0)]=0(ωFωθ)2=1+IPπρ∞b4ℜ[mθ(kF,0)]
上面第一式可以求得颤振边界的减缩频率kF。再代入第二式可以求得颤振边界的振动频率ωF
由减缩频率定义式可以计算颤振速度:
UF=kFbωF
这时给出来流声速c∞,进而计算得到颤振马赫数:
MaF=c∞UF
如果此时计算得到的颤振马赫数接近之前假设的马赫数(第一次迭代为接近零),则可以取此结果。若与之前假设差距过大。则将此颤振马赫数代入(4.1.2)中,重复接下来的步骤。这个迭代方案将收敛于一个颤振边界上的飞行条件。最终得出此高度下的颤振速度UF和振动频率ωF。
4.2 二自由度颤振
这里讨论第3节的模型,如图所示:
与第3节不同的是,本节采用非定常气动理论。则其运动方程类似于(3.4),为:
m(h¨+bxθθ¨)+khh=−LIPθ¨+mbxθh¨+kθθ=M}(4.2.1)
根据第4节开始的分析:
h(t)=hexp(iωt)θ(t)=θexp(iωt)L(t)=Lexp(iωt)M(t)=Mexp(iωt)L=−πρ∞b3ω2[lh(k,Ma∞)bh+lθ(k,Ma∞)θ]M=πρ∞b4ω2[mh(k,Ma∞)bh+mθ(k,Ma∞)θ]
将上面的函数代入到运动方程(4.2.1)中,得:
{πρ∞b2m[1−(ωωh)2]+lh(k,Ma∞)}bh+[πρ∞b2mxθ+lθ(k,Ma∞)]θ=0[πρ∞b2mxθ+mh(k,Ma∞)]bh+{πρ∞b4IP[1−(ωωθ)2]+mθ(k,Ma∞)}θ=0
引入无量纲参数:
μ=πρ∞b2m(质量比)r=mb2IP(关于P点的回转质量半径)
可以简化为:
{μ[1−(ωωh)2]+lh}bh+(μxθ+lθ)θ=0(μxθ+mh)bh+{μr2[1−(ωωθ)2]+mθ}θ=0}(4.2.2)
要使方程有非平凡解,系数行列式为零。同时引入参数σ=ωh/ωθ和λ=(ωθ/ω)2,即:
∣∣∣∣∣μ(1−σ2λ)+lhμxθ+mhμxθ+lθμr2(1−λ)+mθ∣∣∣∣∣=0(4.2.3)
这个行列式被称为“颤振行列式”。其中未知量有λ=(ωθ/ω)2、μ=m/(πρ∞b2)、Ma∞=U/c∞和k=bω/U。同样有ω、ρ∞、U和c∞四个独立变量,且上式有虚部、实部分别等于零两个关系。于是只需要确定其中两个变量,其它变量也可以求得。
下面介绍求解颤振边界的主要步骤:
- 给定一个高度(即给定来流密度ρ∞),则参数μ确定。
- 给定Ma∞的初始值,例如零(即假设来流声速c∞相对于空速U极大,设为不可压缩流)。
- 令颤振行列式等于0,得到关于λ的二次方程。由虚部为零得k值,即kF。
- 将k=kF代入上面二次方程的实部。得到λ的值,即λF=(ωθ/ωF)2。
- 给定来流声速c∞。确定UF=bωF/kF和Ma∞F=UF/c∞。
- 使用步骤5计算的数值Ma∞F重复步骤3~5,直至在给定的μ值下,Ma∞F、kF和UF的值收敛为止。
- 取不同的μ值(即不同高度),重复整个过程确定颤振边界,即给出高度与Ma∞F、kF及UF的变化曲线。
5 颤振问题的工程求解(k法、p-k法)
工程实践中除了求出颤振边界,还有两个着重考虑的问题。第一个,确定在颤振边界附近飞行条件下的稳定裕度;第二个,确定导致不稳定的物理机制。
5.1 k法
在4节的基础上,再引入表征结构阻尼效应的参数。实验观测,在简谐振动中,每个周期消耗的能量与振幅的平方近似成比例,而与频率无关,故可以通过一个与位移成比例、与速度同相位的阻尼力来体现这个特征。
引入阻尼力后运动方程(4.2.1)修正为:
m(h¨+bxθθ¨)+khh=−L+DhIPθ¨+mbxθh¨+kθθ=M+Dθ}
其中耗散阻尼项为:
Dh=Dhexp(iωt)=−ighmωh2hexp(iωt)Dθ=Dθexp(iωt)=−igθIPωθ2θexp(iωt)
于是(4.2.2)修正为:
{μ[1−(ωωh)2(1+igh)]+lh}bh+(μxθ+lθ)θ=0(μxθ+mh)bh+{μr2[1−(ωωθ)2(1+igθ)]+mθ}θ=0}(5.1.1)
注意gh和gθ为人为引入修正参数。可以凭经验预先指定,典型的取值范围为0.01~0.05。这里令gh=gθ=g,并将ω和g合并为一个参数Z:
Z=(ωωθ)2(1+ig)
同样记σ=ωh/ωθ。可得颤振行列式:
∣∣∣∣∣μ(1−σ2Z)+lhμxθ+mhμxθ+lθμr2(1−Z)+mθ∣∣∣∣∣=0(5.1.2)
此方程中有独立未知变量ω、g、ρ∞、U和c∞。而有实部和虚部两个等式关系。可以给定ρ∞(即高度H)和c∞的值,得出函数g=g(U)和ω=ω(U),绘制出函数图像U-g和U-ω。
其中,U-g图像显示出颤振边界附近的飞行条件下的稳定裕度,当g=0时为颤振边界。结合U-ω图像可以得出导致颤振不稳定的物理机理。沿着U=0轴上的频率值对应于初始结构动力学系统耦合模态。随着速度的增加,这些根的个体特征或者他们之间的相互影响体现了能量从一个模态到另一个模态的传递。
5.2 p-k法
5.2.1 p法和k法的比较
现在研究第2节的模型,即:将升力面简化为板模型。
将(2.3)式中的λ消去,得:
[p2diag(M)+U2b2diag(M)diag(ω2)−ρ∞A(p)]ξ=0(5.2.1.1)
其中A(p)为非定常气动算子矩阵,可用(2.3)式中其他矩阵(即a、b、c、d、A和E)表示。
广义振幅要有非平凡解,上式的系数行列式必须为零,即
∣∣∣∣p2diag(M)+U2b2diag(M)diag(ω2)−ρ∞A(p)∣∣∣∣=0(5.2.1.2)
由于(2.3)和(5.2.1.1)是等价的,所以(5.2.1.2)和(2.4)同解。所以(5.2.1.2)的根为:
pl=Ubv=Ub(Γl±iΩl)(l=0,1,⋯,nc,⋯,nc+nr)(5.2.1.3)
而第4节和第5节的k法本质上将v设为iω,且k=bω/U。而k法首先是假定Γl=0,所以k=Ωb/U。
当Ω=0时各典型模态幅值的状态如图
注意,图中exp[(Γk+iΩk)t]表示的是由两个共轭复根exp[(Γk±iΩk)t]导出的一对等价实根exp(Γkt)cos(Ωkt)和exp(Γkt)sin(Ωkt)中的前者。即:
exp[(Γk±iΩk)t]=exp(Γkt)[cos(Ωkt)±isin(Ωkt)]2exp(Γkt)[cos(Ωkt)+isin(Ωkt)]+exp(Γkt)[cos(Ωkt)−isin(Ωkt)]=exp(Γkt)cos(Ωkt)2iexp(Γkt)[cos(Ωkt)+isin(Ωkt)]−exp(Γkt)[cos(Ωkt)−isin(Ωkt)]=exp(Γkt)sin(Ωkt)
假设t0和t0+T为图中某两个相邻波峰的时间(cos(Ωt0)=1、cos[Ω(t0+T)]=1)。设am和am+1为连续周期的振幅。则:
am=exp(Γt0)cos(Ωt0)=exp(Γt0)am+1=exp[Γ(t0+T)]cos[Ω(t0+T)]=exp[Γ(t0+T)]
则:
ln(amam+1)=ΓT
又周期T=2π/Ω,所以
Γ=2π1ln(amam+1)Ω
令γ=ln(am+1/am)/(2π),命名为衰减率。则
pl=Ubv=Ub(Γl±iΩl)=UbΓl±iUbΩl=γUbΩ±iUbΩl
已推得k=Ωb/U。所以:
p=γk±ik(5.2.1.4)
于是令(5.2.1.3)中p=ik,可得颤振行列式:
∣∣∣∣−k2diag(M)+U2b2diag(M)diag(ω2)−ρ∞A(ik)∣∣∣∣=0
其中独立未知变量有Ω、U、ρ∞、g(k法会引入一个阻尼参数)和c∞,而有实部和虚部两个关系式。于是在给定ρ∞(高度)和c∞时得出函数g=g(U)和Ω=Ω(U),绘制出函数图像U-g和U-Ω。
经过分析,阻尼参数g和衰减率γ关系为:
g≅2γ
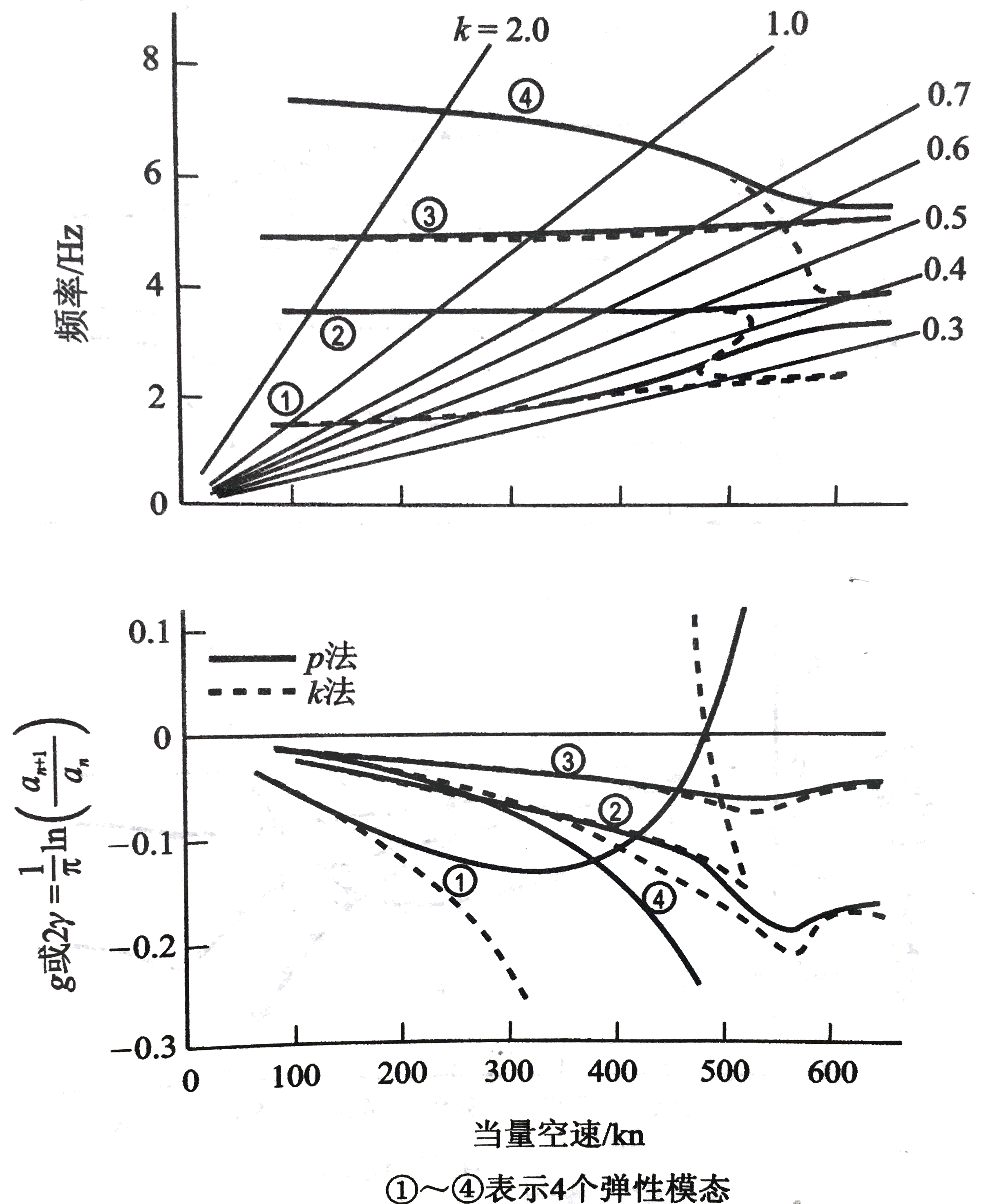
可以看出,k法在分析颤振附近的飞行条件时,将原本p中的阻尼项γk略去,而人为加上了一个阻尼参数g进行修正。然而这个修正并不能完全符合原方程关系。如图所示为p法和k法计算相同的模型得出的曲线。
k法不仅得出错误的模态耦合,而且更重要的是,得出了错误的不稳定模态。这两种分析唯一一致有效的结果是在g=γ=0点处所对应的颤振速度。
尽管k法给出了不一致的模态耦合,但是它可以使用非定常气动力的简谐模型。简谐运动载荷的计算精度优于瞬态运动气动载荷的计算精度。于是产生了两种方法的折中。
5.2.2 p-k法简介
p-k法就是这样一种折中。它基于p法进行颤振分析,但使用简谐运动的非定常气动力矩阵。使用k值来计算矩阵A(ik),颤振行列式为
∣∣∣∣p2M+U2b2Mω2−ρ∞A(ik)∣∣∣∣=0
求解方法如下:
- 给定一组k的初始估计值,比如对于第i个根,k0=bωi/U。
- 将k0代入方程中,解出p。
- 由于p是简单出现在方程中的,所以以上方程可以看作关于p的标准特征值问题。典型解是一组共轭复根对。选择其中的一个根,初始解记为:
k1=∣ℑ(p)∣,γ1=k1ℜ(p)
- 将新解得的k1代入方程中,重复步骤2~3,直到每一个根收敛。
对于低阶问题的求根过程,可以取k=∣ℑ(p)∣时的行列式为零。
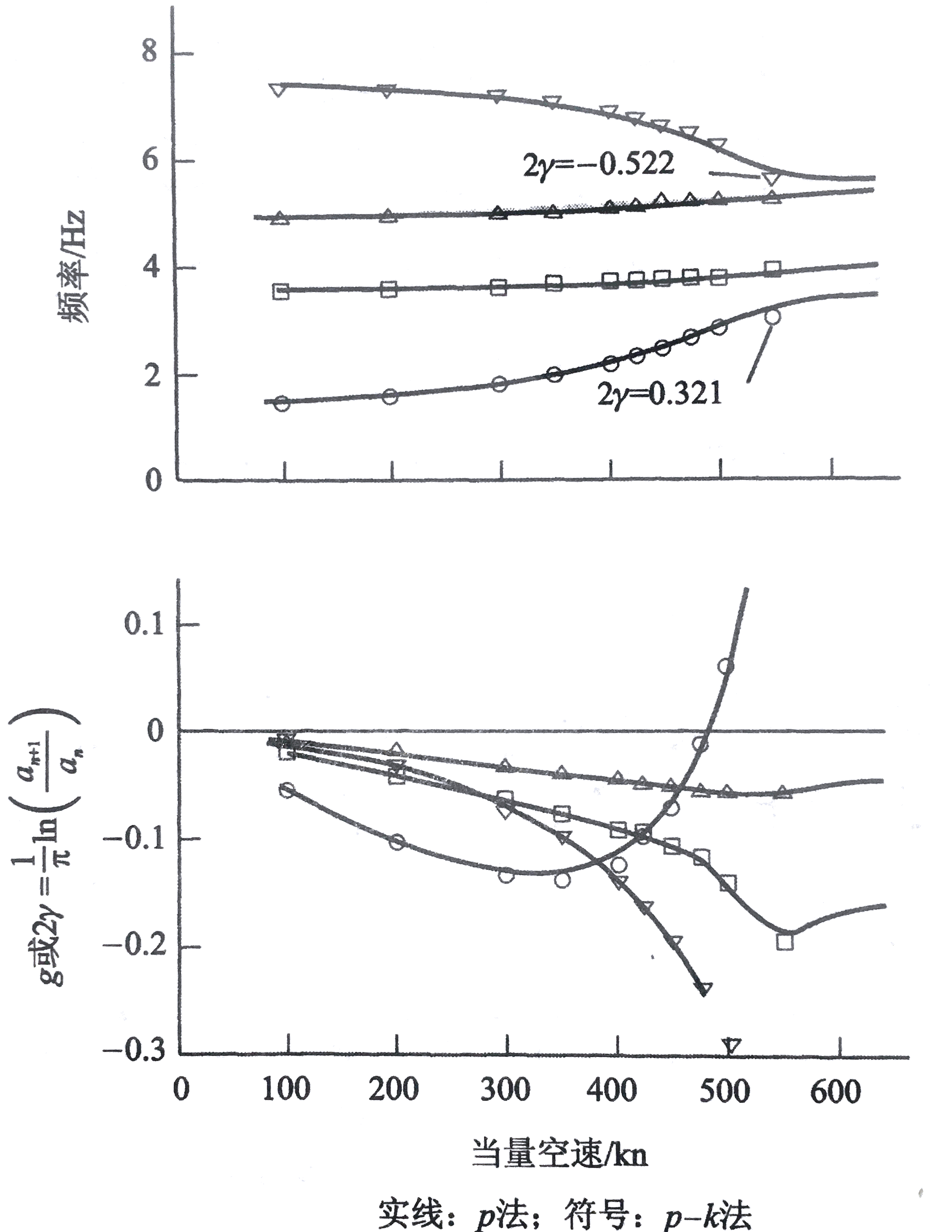
用p法和p-k法计算5.2.1节的模型,得曲线如图所示:
p-k法得到了于p法几乎相同的结果。p-k法的最大优势在于它可以使用简谐运动形式的气动载荷。
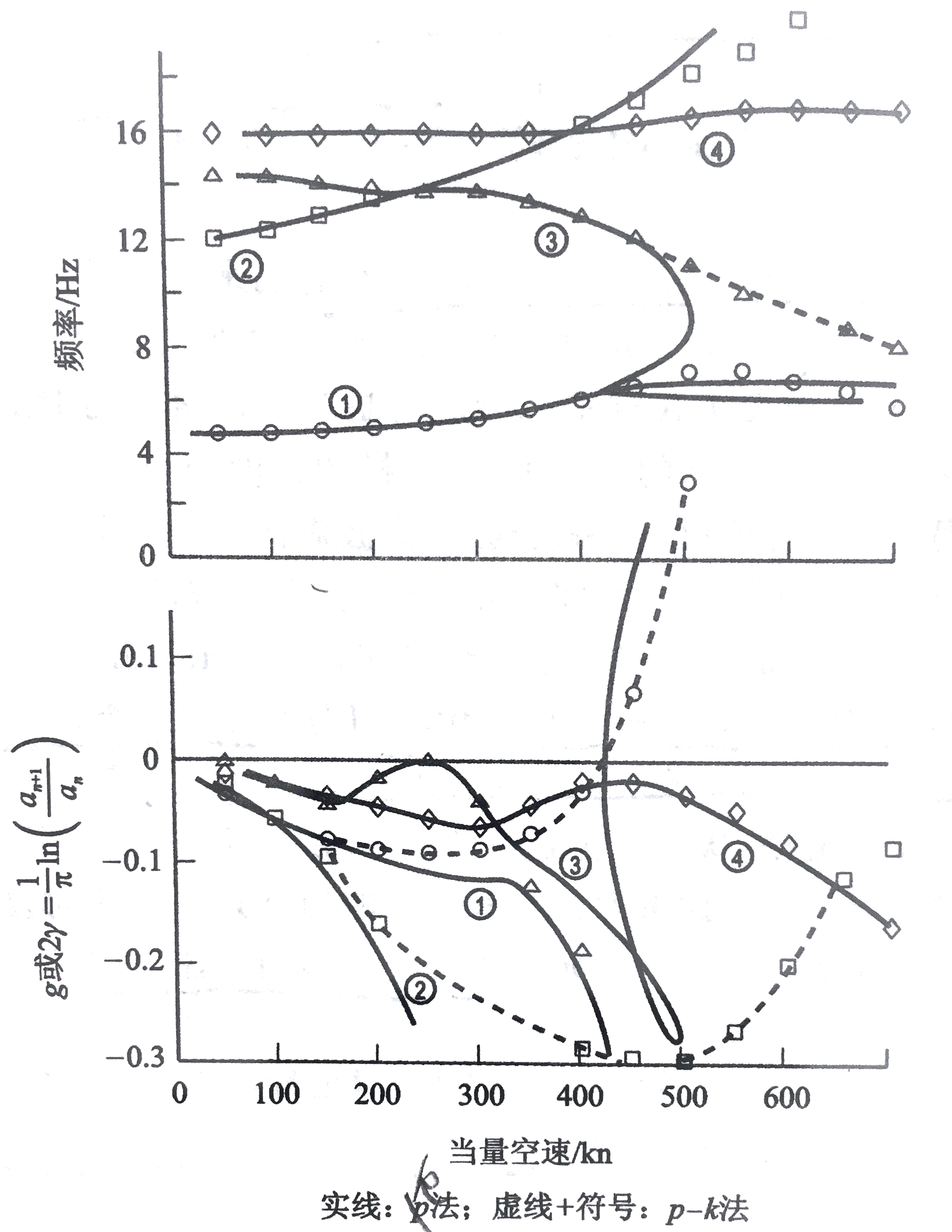
将k法和p-k法用在水平安定面/升降舵构型的颤振分析中。这是一个强耦合的系统。分析结果如图所示:
这里也得到了大相径庭的模态耦合结论。p-k法除了对强耦合系统很容易分析频率-速度和阻尼-速度曲线外,它的第二个优势在于计算耗费。在密度不变的情况下,k法需要大量的运算,以确保马赫数与速度和高度匹配,而p-k法则不需要。
6 非定常气动力
在第3节使用定常气动理论进行颤振分析时,升力和俯仰力矩仅是瞬时俯仰角θ的函数。然而深入探究,很容易看出攻角并不简单地就等于θ。例如,翼型参考基准点以速度h˙做沉浮运动,可以论证至少对于小角度,应修正攻角以变引入沉浮影响,即
α=θ+Uh˙
这源于考虑飞机滚转对机翼攻角的影响。但必须小心做此特定的推论,因为可能还有其他同等量级的影响没有考虑。
在非定常流场中,升力和俯仰力矩由两部分构成——非环量效应和环量效应。
环量效应通常对机翼更加重要。事实上,在定常飞行中,是环量产生的升力使飞机在空中飞行。回顾Helmholtz定理:在任意包围特定流体微团的封闭曲线内,总涡量始终为零。因此,如果一个顺时针涡量随机翼发展变化,那么一定有相同强度的逆时针漩涡脱落到流动中。随着脱落涡运动、发展,它会诱导产生非定常流动,从而改变流场,反过来影响机翼。在估算这些脱落涡的影响时,可以假设脱落涡随来流一起运动,简化运算。
非环量效应,也称为视在质量和惯性效应,重要性次于环量效应。当机翼有加速度时会产生非环量效应,而且会因此带动部分周围的空气随之运动,这部分空气具有确定的质量,会产生与其加速度对应的惯性力。
总而言之,非定常气动理论需要考虑至少以下三个独立的物理现象:
- 风速方向的变化改变了有效攻角,从而改变了升力。
- 机翼的运动对气流有扰动,并使漩涡自后缘脱落。脱落涡产生的下洗,反过来会改变机翼的绕流。这个非定常下洗改变了有效攻角,从而改变了升力。
- 机翼的运动会使翼表面附近的空气微团加速运动,因此需要考虑由此产生的惯性力。
6.1 Theodorsen非定常薄翼理论
Theodorsen(1934年)推导了小简谐振动情况下不可压流的薄翼(平板)非定常气动理论。
根据Theodorsen理论,升力和俯仰力矩可表示为
L=2πρ∞UbC(k)[h˙+Uθ+b(21−a)θ˙]+πρ∞b2(h¨+Uθ˙−baθ¨)M41=−πρ∞b3[21h¨+Uθ˙+b(81−2a)θ¨]}(6.1.1)
函数C(k)是减缩频率k的复数函数,可表示为
C(k)=H1(2)(k)+iH0(2)(k)H1(1)(k)
其中Hn(2)(k)是第二类Hankel函数,可以分别由第一类和第二类Bessel函数表示为
Hn(2)(k)=Jn(k)−iYn(k)
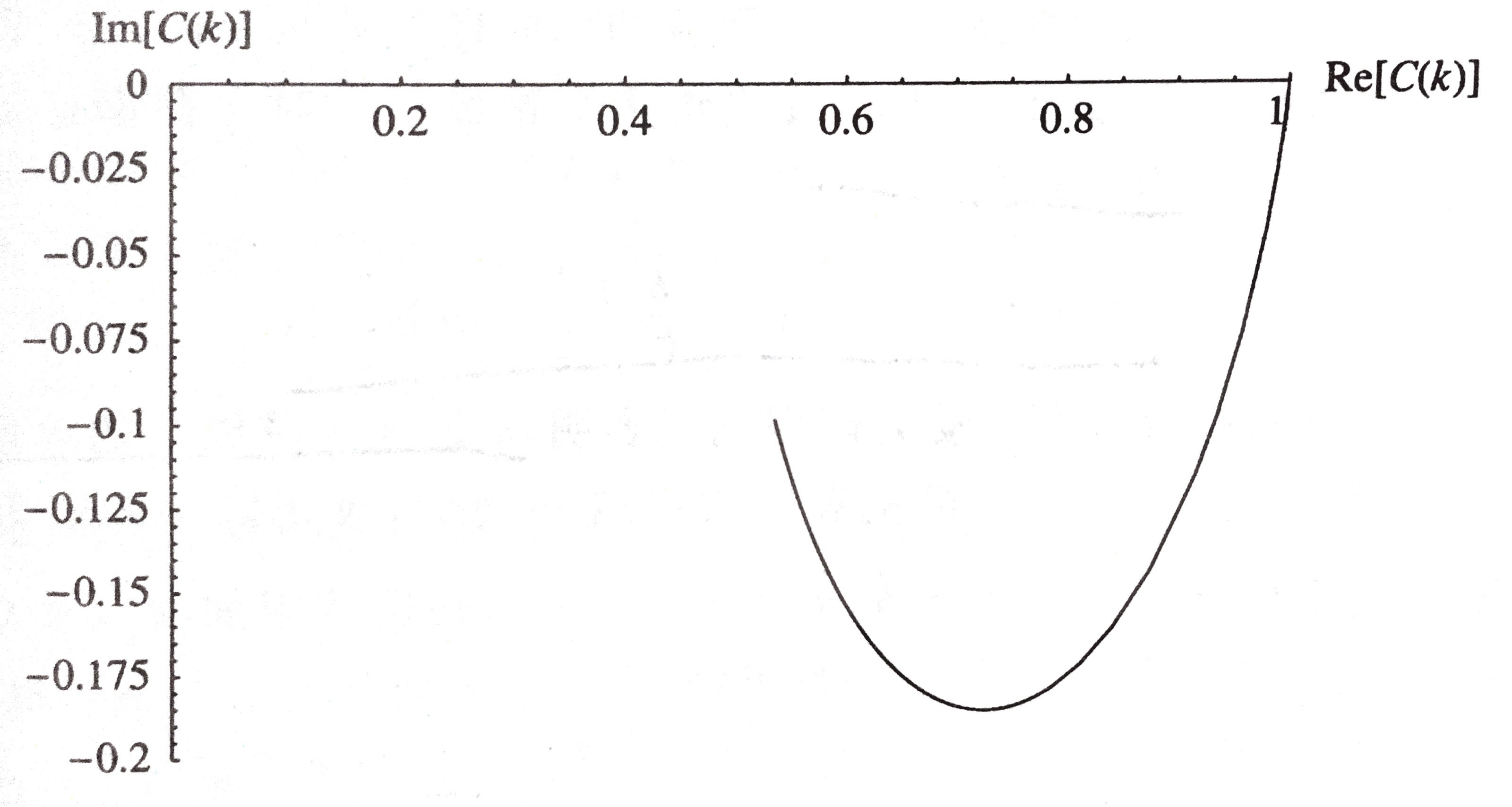
函数C(k)=F(k)+iG(k)称为Theodorsen函数。k从0变化到1时C(k)的实部和虚部曲线如图所示:
注意对于定常情况(即k=0),而且等于1。随着k增加,虚部也增加,实部减小;当k趋于无穷大时,C(k)接近于1/2。但在实际情况中,k不会超过1,所以图中只绘制了直到k=1的情况。任何一个调和函数乘以C(k)后,数值都会减小,同时都会产生相位滞后。
下面对升力和俯仰力矩表达式简要分析介绍:
Theodorsen理论推导基于线性势流理论,升力线斜率等于2π。
升力表达式的第一项式环量升力(不考虑脱落效应)乘以C(k),这是为了考虑脱落涡的影响。
非环量项(即升力表达式第二项和全部俯仰力矩)取决于机翼的加速度和角加速度。注意到,升力中h¨的系数是以b为半径的单位长度的圆柱(无限长圆柱)所含的空气质量,它反映了因机翼运动使多少空气获得加速度。
对于定常流,环量升力与攻角呈线性关系。对于非定常流和简谐运动,可以从Theodorsen理论中推出有效攻角:
α=C(k)[θ+Uh˙+Ub(21−a)θ˙]
通过与有限状态气动力模型比较表明,这是3/4弦线处的攻角。
注意:一般而言Theodorsen理论只在简谐振动条件下才有效,是频域微分方程。
但当C(k)等于1时,Theodorsen理论的近似称为“准定常”薄翼理论。这样的近似仅当k取值非常小时才适用。对于缓慢的简谐运动或缓慢的非简谐的变化运动,准定常理论可以用于时域。
Theodorsen理论可以用于k法和p-k法。
6.2 Peter等人的有限状态非定常薄翼理论
在进行颤振分析时,通常需要计算亚临界飞行条件下的模态阻尼;在颤振主动控制设计中,控制器的设计要求系统可表示为状态空间形式。为了满足这些要求,需要用时域微分方程来表示真实的气动载荷(Theodorsen的理论中为频域)。
有限状态理论是在工程精度范围内对真实的无线状态的空气动力模型进行近似。其中一个方法是Peter等人(1955年)提出的针对无粘不可压流的有限状态诱导流理论。
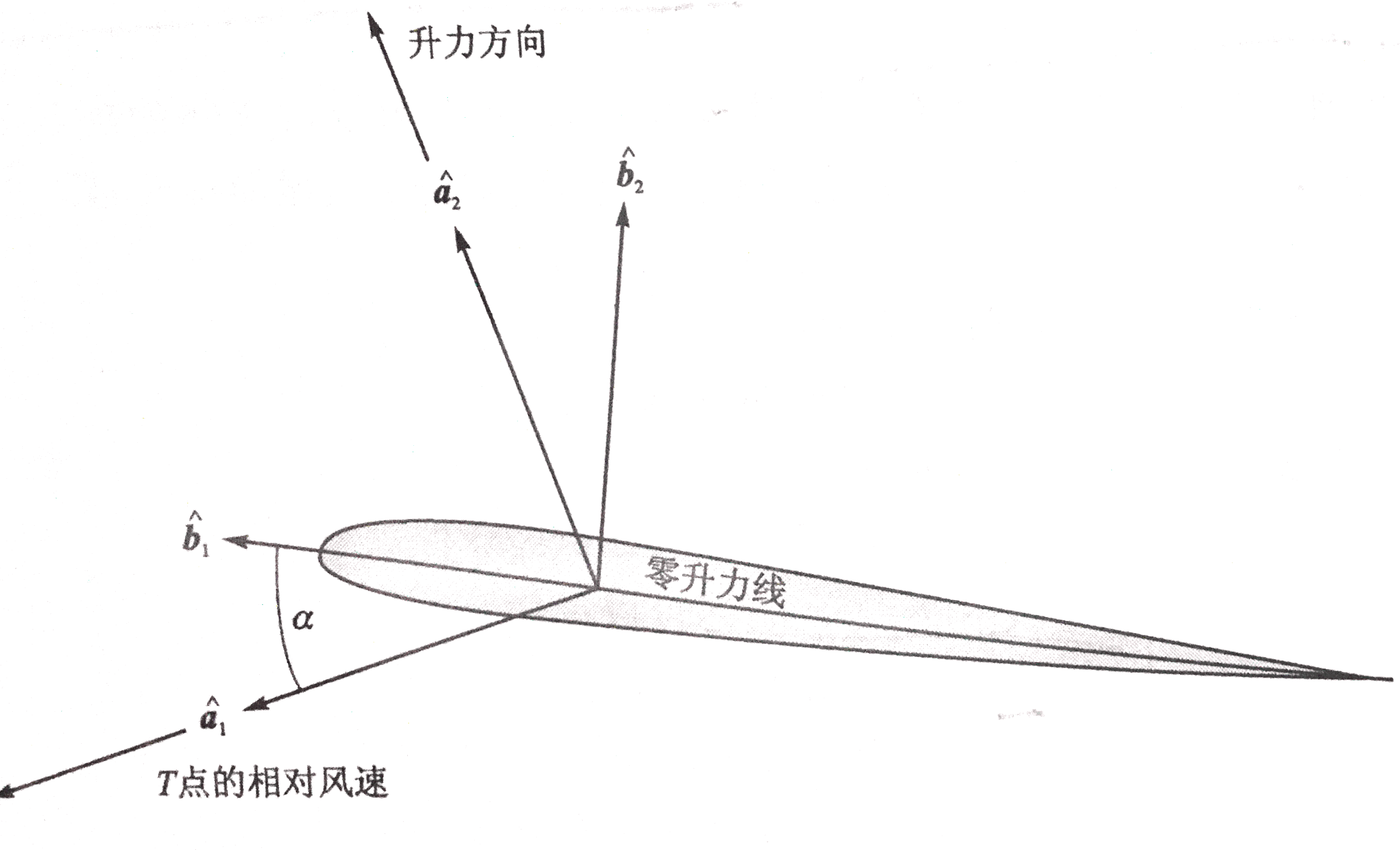
考虑一个刚硬、对称机翼的典型剖面,如图所示。
附加矢量方向定义。如图所示:
其中有三组单位矢量:
- 固定于惯性系的一组矢量i1和i2,则空气流动速度为−Ui1;
- 固定于机翼的一组矢量b1和b2,其中b1沿着零升力线指向前缘,b2垂直于b1;
- 与3/4弦线处(T点)的当地相对风速矢量相关的一组矢量a1和a2,a1沿着相对风速矢量的方向,a1和a2垂直,沿着假定的升力方向。
这些单位矢量之间的关系可以表示为:
[b1b2]=[cosθ−sinθsinθcosθ][i1i2],[a1a2]=[cosθsinθ−sinθcosθ][b1b2],i3=a3=b3=b1×b2
诱导流理论以脱落涡引起的翼型附近流场的改变为基础,对脱落涡的影响进行了近似。因此,翼型附近的速度场包含自由流速度和用来描述诱导流的额外速度分量。并将诱导流近似为弦线方向上的平均值。以此当地的惯性风速可以写为−Ui1−λ0b2,这里λ0是平均诱导流速度(垂直于翼型的零升力线)。根据经典薄翼理论,应该使用T点的瞬时相对风速来计算攻角α。T点相对风速Wa1可以写作:
Wa1=vT−(−Ui1−λ0b2)=vT+Ui1+λ0b2
其中vT是3/4弦长处的惯性速度,表达式为
vT=vP+θ˙b3×rPT
rPT是从P点到T点位置矢量。从图中可以看出:
rPT=[2b+(1+a)b−2b]b1=b(a−21)b1
vP是P点的惯性速度:
vP=−h˙i2
θ˙b3为机翼的惯性角速度。
所以
vT=−h˙i2+bθ˙(a−21)b2
代入相对风速的表达式:
Wa1=Ui1−h˙i2+[bθ˙(a−21)+λ0]b2
于是:
Wa1⋅b1=Ucosθ−h˙sinθWa1⋅b2=−Usinθ−h˙cosθ+bθ˙(a−21)+λ0}(6.2.1)
另外,由矢量关系:
Wa1=Wcosαb1−Wsinαb2
于是:
Wa1⋅b1=WcosαWa1⋅b2=−Wsinα}(6.2.2)
对比(6.2.1)和(6.2.2)得:
Wcosα=Ucosθ−h˙sinθ−Wsinα=−Usinθ−h˙cosθ+bθ˙(a−21)+λ0
θ和α为小角度,则可设:
sinθ=θsinα=αcosθ=1sinα=1αθ=0
上式可变为:
W=U−h˙θ−Wα=−Uθ−h˙+bθ˙(a−21)+λ0
解上面方程,注意αθ=0:
α=θ+Uh˙+Ub(21−a)θ˙−Uλ0W=U−h˙θ}(6.2.3)
可见,攻角α取受俯仰角速度、沉浮速度和诱导流影响。
上述考虑了风速方向改变和漩涡脱落两个因素(即环量效应的因素)改变了有效攻角从而引起的非定常特性。除此之外还有非环量效应因素引起的非定常特性。如果将三者共同考虑,将会升力和力矩表达式:
L=2πρ∞Ub[h˙+Uθ+b(21−a)θ˙−λ0]+πρ∞b2(h¨+Uθ˙−baθ¨)M41=−πρ∞b3[21h¨+Uθ˙+b(81−2a)θ¨]}(6.2.4)
但其中有一个未确定量λ0,即需要将λ0用机翼运动表示。Peter等人的诱导理论的做法是:用N个诱导流速度λ1,λ2,⋯,λN来表示平均诱导速度λ0。如:
λ0≈21n=1∑Npnλn
其中pn由最小二乘法求得。N是由计算者给定。
假设脱落涡保持在机翼平面,并且以同样的速度随气流顺流而下,由此可以推导出诱导流的动力学方程:
Aλ˙+bUλ=c[h¨+Uθ˙+b(21−a)θ¨]
其中:
λ=(λ1λ2⋯λN)TA=D+dbT+cdT+21cbTDnm=⎩⎪⎪⎨⎪⎪⎧2n1,(n=m+1)−2n1,(n=m+1)0,(n=m±1)bn={(−1)n−1(N−n−1)!(N+n−1)!n!12,(n=N)(−1)n−1,(n=N)dn={21,(n=1)0,(n=1)cn=n2
求解上面的一阶常微分方程就可以得到λ1,λ2,⋯,λN的表达式,进而求得λ0的表达式。
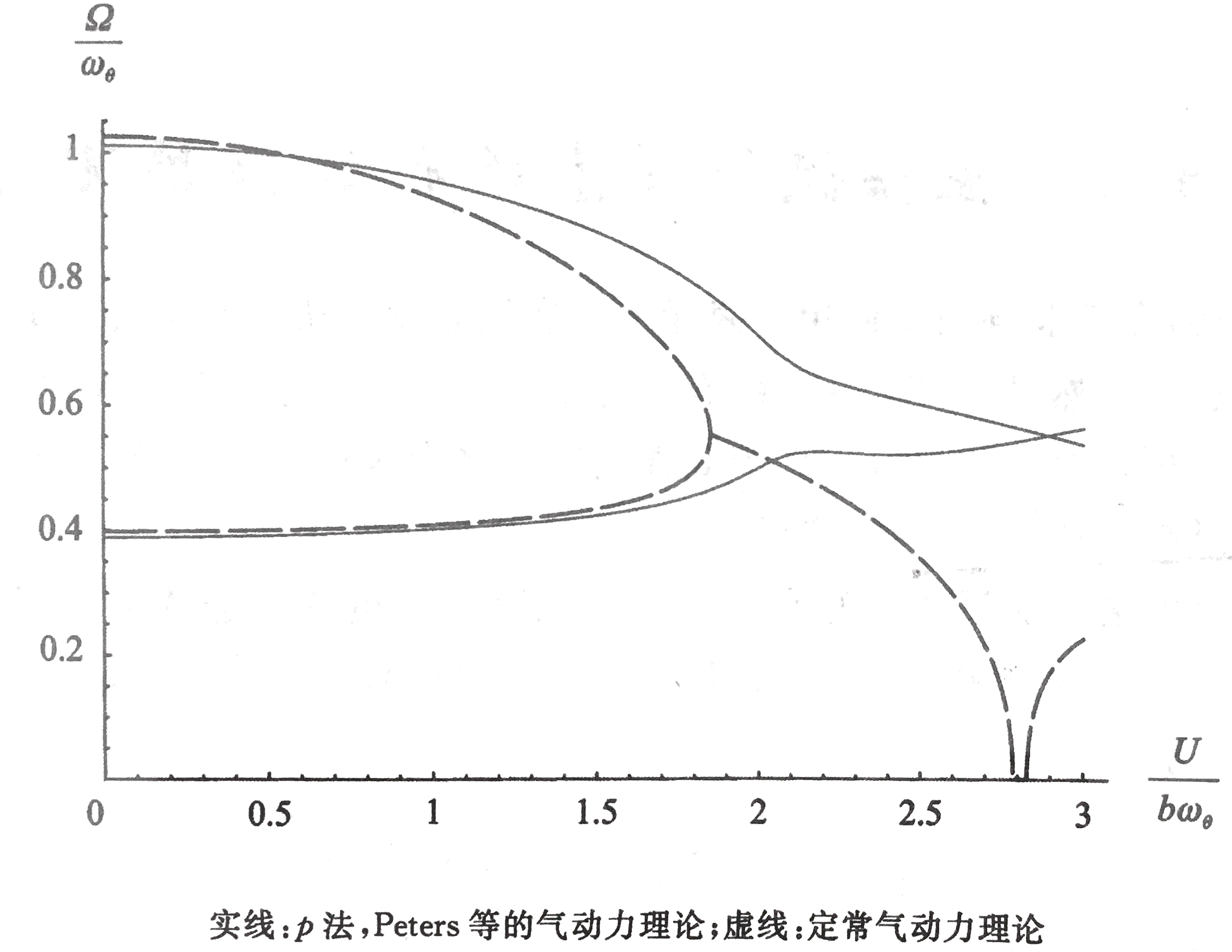
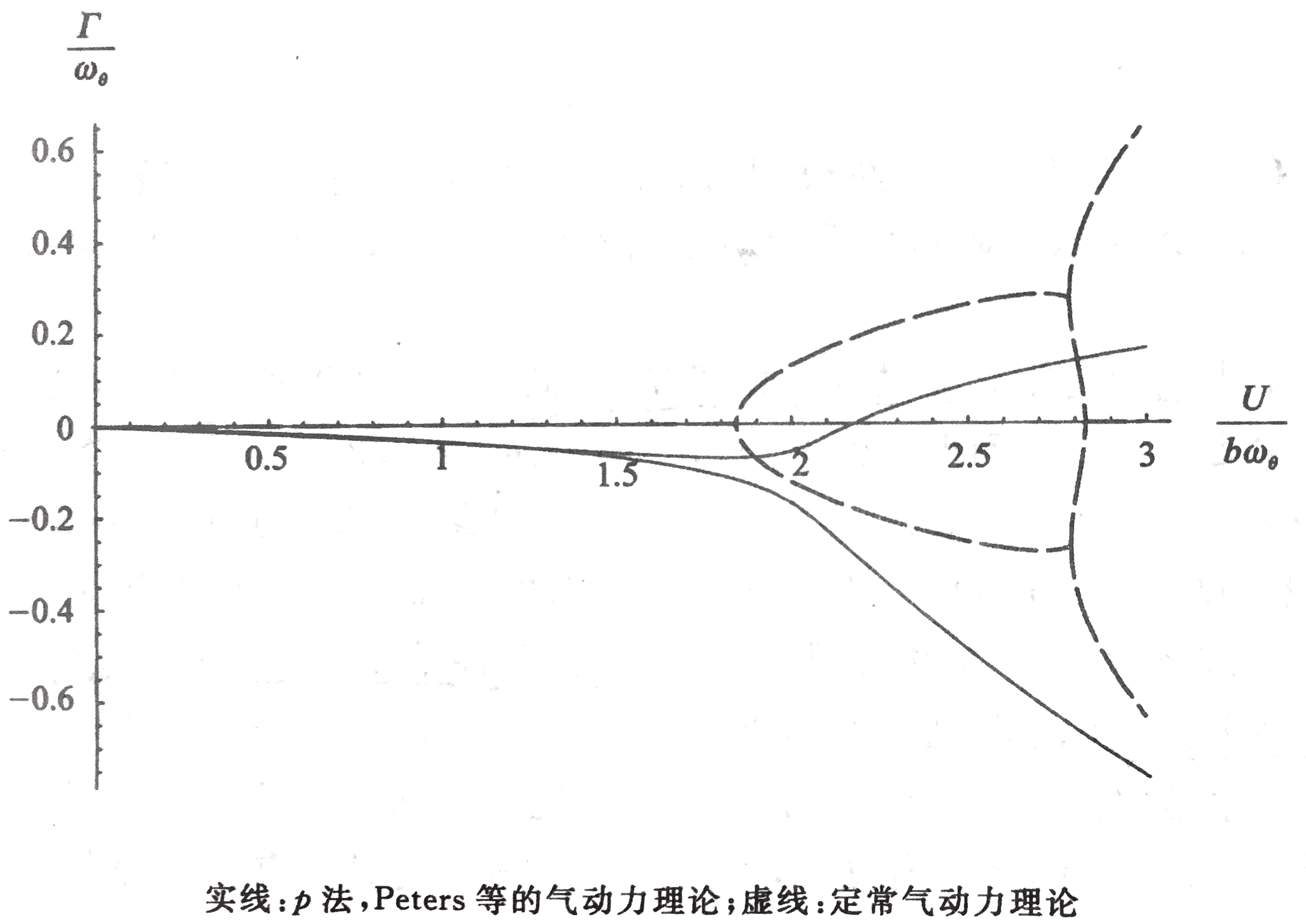
将本小节的有限状态非定常薄翼理论引入第3节的模型。即将(6.2.4)式代入(3.4)式中,对第3节中的算例(a=−1/5e=−1/10μ=20r2=6/25σ=2/5)进行结果分析,分析时选取N=6个诱导流速度。频率和阻尼分析结果如图所示:
与之前类似,在接近不稳定时,可以观察到有频率相互靠近的趋势,但是颤振条件式以某一个根的实部穿越过横轴成为正值来确定的,从而得到颤振速度VF=UF/(bωθ)=2.165,颤振频率ΩF/ωθ=0.6545。
7 根据假设模态进行颤振预测
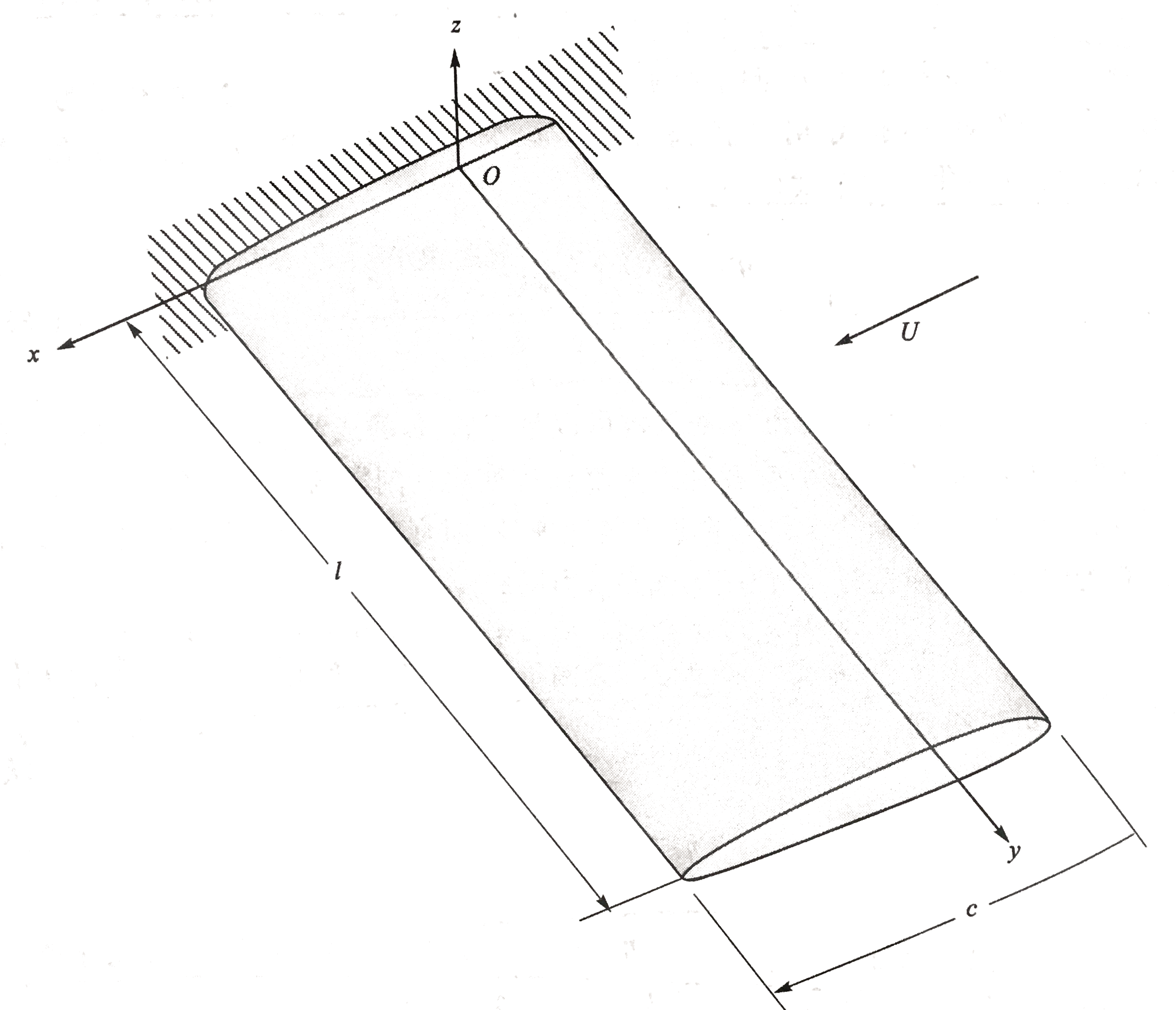
考虑一个安装在风洞壁上的非后掠机翼,用长为l的均匀悬臂梁模拟,如图所示:
因此对于一个具有弯曲刚度为EI和扭转刚度GJ的梁,其应变能为:
U=21∫0l[EI(∂y2∂2w)2+GJ(δyδθ)2]dy(7.1)
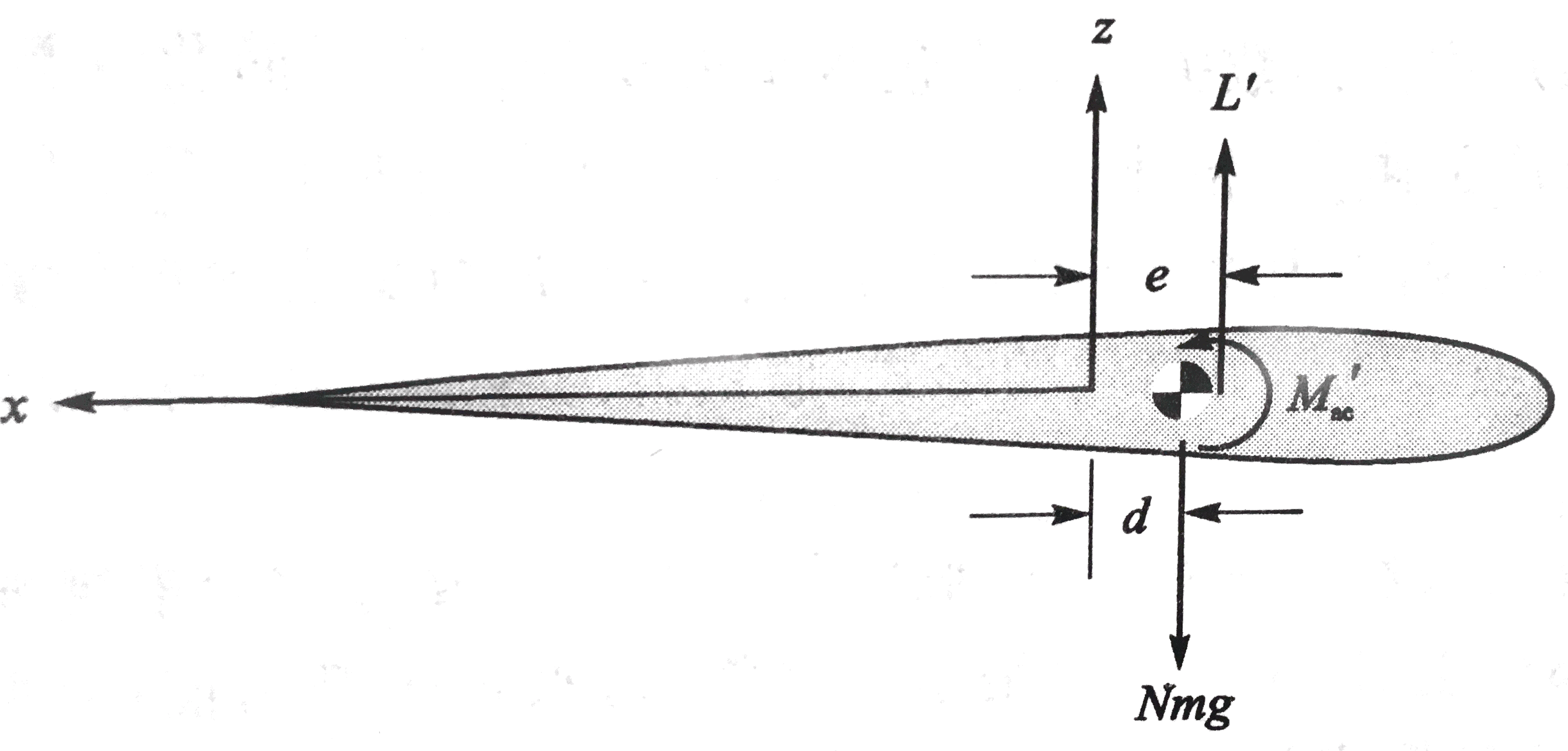
其翼剖面如图所示:
材料密度为ρ,横截面内典型点的速度为
v=z∂t∂θi+(∂t∂w−x∂t∂θ)k
i和k分别是x和y方向上的单位矢量,则动能可表示为
K=21∫0l∬Aρ[(∂t∂w−x∂t∂θ)2+z2(∂t∂θ)2]dxdydz=21∫0l[m(∂t∂w)2+2md∂t∂w∂t∂θ+mb2r2(∂t∂θ)2]dy
其中,m是单位长度质量,d是质心与弹性轴之间的距离(当质心朝向前缘为正),b是半弦长,br是截面质量绕弹性轴的回转半径。
气动力所做的虚功为:
δW=∫0l[L′δw+(Mac′+eL′)δθ]dy
上面使用的符号是静气动力学的符号习惯。现在改为非定常气动力学符号习惯。
d→−bxθe→(21+a)bL′→L′Mac′→M41′
动能变为:
K=21∫0l[m(∂t∂w)2−2mbxθ∂t∂w∂t∂θ+mb2r2(∂t∂θ)2]dy(7.2)
虚功变为:
δW=∫0l{L′δw+[M41′+(21+a)bL′]δθ}dy(7.3)
合理的假设模态是选择一组不耦合的悬臂梁的自由弯曲和和扭转模态:
w(y,t)=∑i=1Nwηi(t)Ψi(y)θ(y,t)=∑i=1Nθϕi(t)Θi(y)}(7.4)
其中,Nw和Nθ分别表示弯曲模态和扭转模态的个数,ηi和ϕi分别是与弯曲和扭转相关的广义坐标,Ψi和Θi分别是弯曲和扭转模态振型。且:
Θi=2sin(γiy)Ψi=cosh(αiy)−cos(αiy)−βi[sinh(αiy)−sin(αiy)]
其中,γi=π(i−1/2)/l,而αi和βi满足:
cos(αl)cosh(αl)+1=0βi=sinh(αil)+sin(αil)cosh(αil)+cos(αil)
将(7.4)代入(7.1)和(7.2)中,利用弯曲和扭转二者模态存在正交性可简化得:
U=21[l3EIi=1∑Nw(αil)4η˙i2+lGJi=1∑Nθ(γil)2ϕi2](7.5)
K=2ml(i=1∑Nwη˙i2+b2r2i=1∑Nθϕ˙i2−2bxθi=1∑Nθi=1∑NwAijϕi˙ηi˙)(7.6)
其中
Aij=l1∫0lΘiΨjdy(i=1,2,⋯,Nθ;j=1,2,⋯,Nw)
将(7.4)代入(7.3)得
δW=i=1∑Nwδηi∫0lΨiL′dy+i=1∑Nθδϕi∫0lΘi[M41′+(21+a)bL′]dy
于是广义力为
Ξwi=∫0lΨiL′dyΞθi=∫0lΘi[M41′+(21+a)bL′]dy}
由Theodorsen理论(6.1.1)式(注意h=−w)得
L′=2πρ∞UbC(k)[Uθ−∂t∂w+b(21−a)∂t∂θ]+πρ∞b2(U∂t∂θ−∂t2∂2w−ba∂t2∂2θ)M41′=−πρ∞b3[U∂t∂θ−21∂t2∂2w+b(81−2a)∂t2∂2θ]}
将上式和(7.4)式代入前面一个广义力表达式中,写成矩阵的形式:
[ΞwΞθ]=−πρ∞b2l[EbaAbaATb2(a2+81)E][η¨ϕ¨]−πρ∞bUl[2C(k)E2b(21+a)C(k)A−b[1+2(21−a)C(k)]ATb2(21−a)[1−2(21+a)C(k)]E][η˙ϕ˙]−πρ∞bU2l[00−2C(k)AT−b(1+2a)C(k)E][ηϕ](7.7)
其中A由Aij组成,E表示单位矩阵,0表示零矩阵。
将(7.5)、(7.6)和(7.7)代入拉格朗日方程得到广义运动方程,写成矩阵的形式:
ml[E−bxθA−bxθATb2r2E][η¨ϕ¨]+[l3EIdiag(B)00lGJdiag(T)][ηϕ]=[ΞwΞθ](7.8)
其中对角矩阵diag(B)和diag(T)的元素为
Bij=(αil)4Tij=(γil)2
由于Theodorsn理论的局限性,这个运动方程金对简谐运动有效。则可以用于第4节经典颤振分析的方法,即令:
η˙(t)=ηexp(iωt)ϕ˙(t)=ϕexp(iωt)}
其中ω是简谐运动的频率。这样就可以导出颤振行列式,并求得颤振速度。
下面考虑Nw=Nθ=1的情况,类似于第4节,写出一个类似与(4.2.2)式:
{μ[1−(ωωw)2]+lw}bη1+(−μxθ+lθ)A11ϕ1=0(−μxθ+mw)bη1+{μr2[1−(ωωθ)2]+mθ}ϕ1=0}
其中:
μ=πρ∞b2mlw=1−k2iC(k)lθ=a+ki[1+2(21−a)C(k)]+k22C(k)mw=a−k2i(21+a)C(k)mθ=a2+81−k(21−a)[1−2(21+a)C(k)]i+k22(21+a)C(k)ωw=(α1l)2ml4EIωθ=2πmb2r2l2GJA11=0.958641
则可以写出颤振行列式:
∣∣∣∣∣μ[1−(ωωw)2]+lw(−μxθ+mw)A11(−μxθ+lθ)A11μr2[1−(ωωθ)2]+mθ∣∣∣∣∣=0
由此可以按照第4节的方法求得颤振边界。
8 颤振边界特性
由前面的章节介绍了以高度、速度和马赫数表示的颤振边界。给定一个飞行器,其颤振速度常与高度、来流声速有关。颤振速度通常用无量纲减缩速度V=U/(bωθ)表示,称为减缩颤振速度VF=UF/(bωθ)。高度通常由质量比μ=m/(πρ∞b2)表示(来流密度ρ∞是高度的函数)。来流声速通常用来流马赫数Ma∞=U/c∞表示。
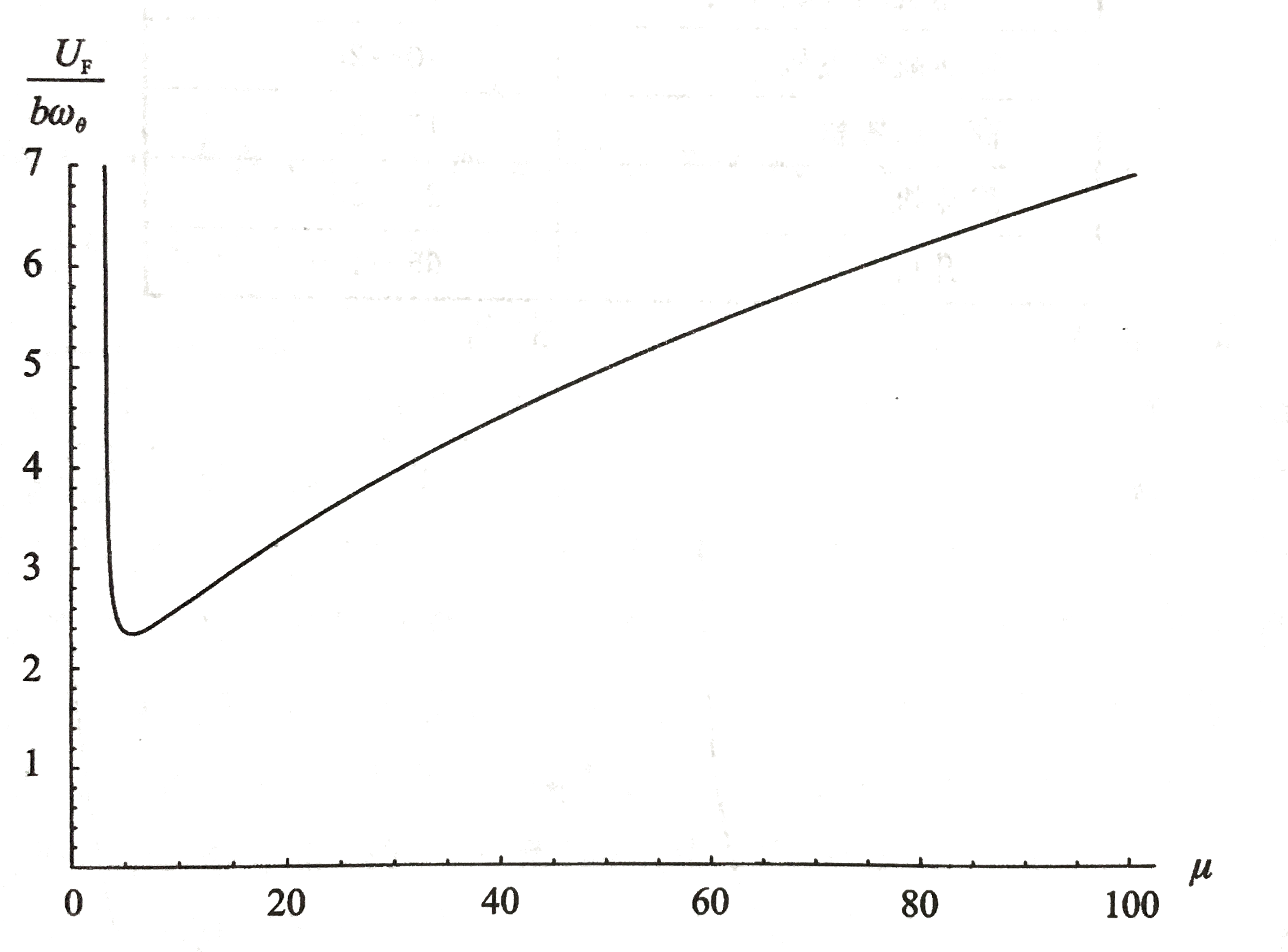
来流马赫数一定时,VF和μ的关系如图所示(σ=1/10,r=1/2,xθ=0,a=−3/10):
可以看出,颤振速度随着质量比的增加几乎线性增加。意味着飞行器在低空时要比高空时更容易颤振。
对于不同的飞行器,颤振边界也对结构参数非常敏感。
升力面单位展长的质量m影响着质量比μ=m/(πρ∞b2)。下表为大气密度为从海平面到10000英尺之间飞行器的构型及其典型质量比数值:
| 飞行器类型 | μ |
|---|---|
| 滑翔机和轻型飞机 | 5~15 |
| 普通航空飞机 | 10~15 |
| 商用运输机 | 15~30 |
| 战斗机 | 25~55 |
| 直升机叶片 | 65~110 |
可见滑翔机和轻型飞机更易发生颤振。
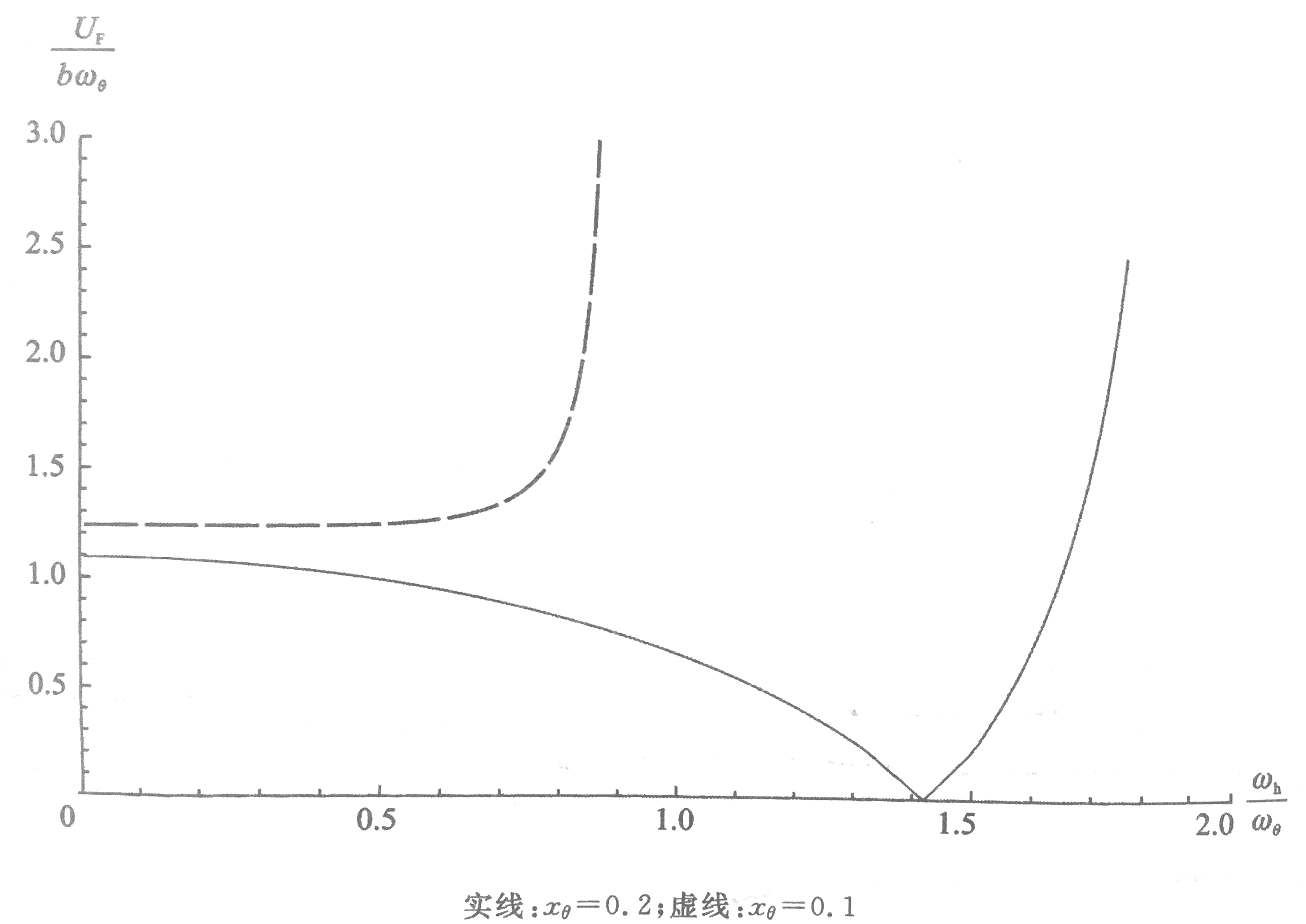
在质量比非常小的情况下,颤振速度随频率比σ=ωh/ωθ的变换十分剧烈。如图所示无量纲颤振速度随频率比的变化曲线(μ=3,r=1/2,a=−1/5):
当xθ=0.2时,σ=1.4附近的颤振速度陡然降至极小,这一点具有最重要的实际意义。受其他参数影响,在某些频率比处,颤振速度会变得很低。这类凹坑可以大多数高性能飞机机翼的颤振速度随频率比的变化曲线看到,这类飞机具有相对较大的质量比μ和正的静不平衡xθ。
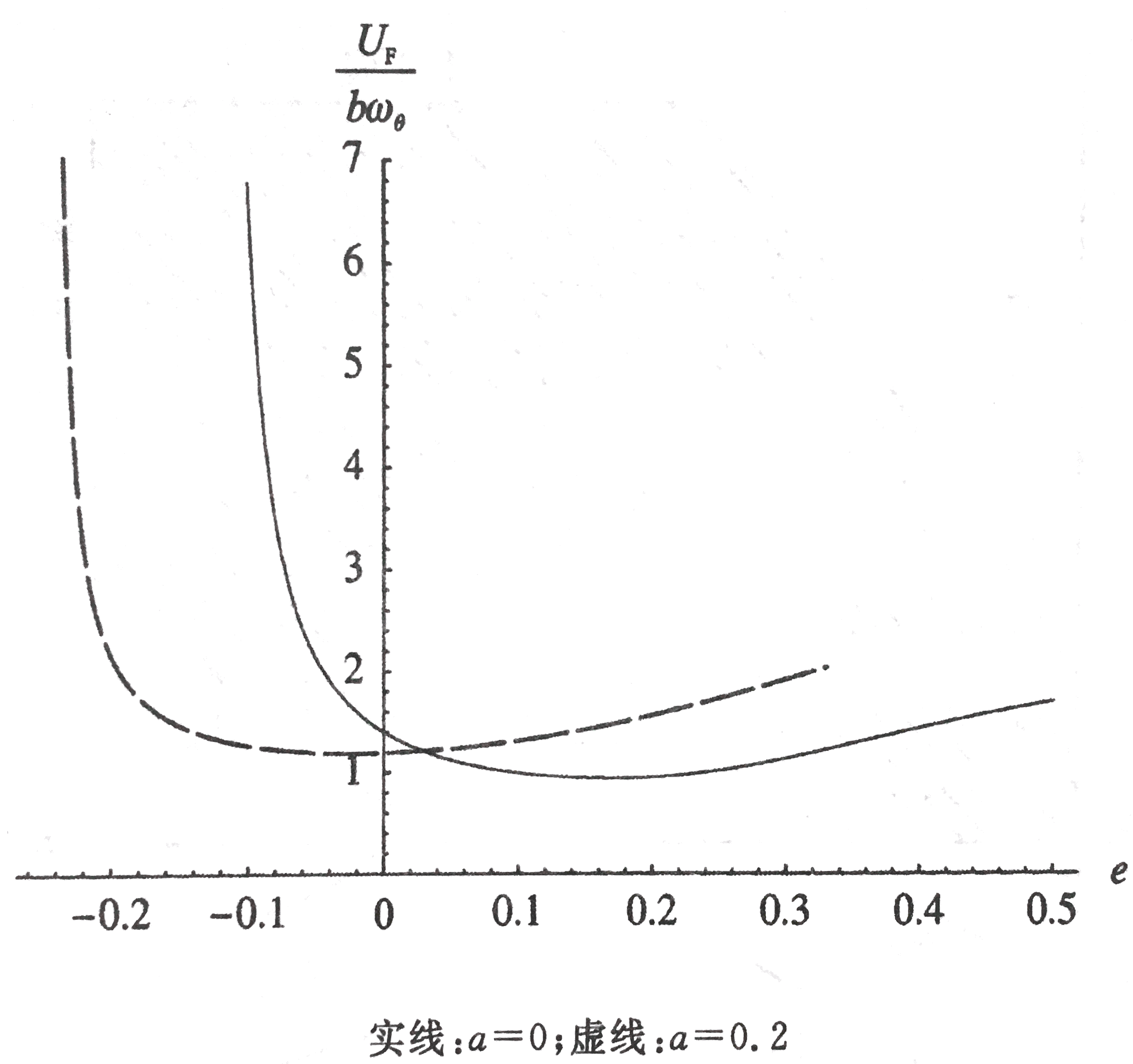
弦向的无量纲距离参数(见第3节的模型)同样对颤振速度有很强的影响,如图所示无量纲颤振速度随e的变化曲线(μ=10,σ=1/2,r=1/2):
质心位置e和无量纲回转半径r必然同时改变,但是前者小百分比变化对颤振速度造成的影响要大于后者同样百分比变化对颤振速度造成的影响。如果质心相对于参考点前移,那么颤振速度通常会提高。
最后,注意到弯扭耦合型颤振频率介于ωh和ωθ之间,即通常σ<1,不过也有可能出现颤振频率高于ωθ的情况。
值得注意的是,目前的简化理论表明,在弦向偏移参数e和a的某些组合下不会发生颤振。当σ取小值时,若e≤−1/2则不会发生颤振;当σ取大值时,若a≥−1/2则不会发生颤振。当质心、弹性轴和气动中心三者全部重合(即e=a=−1/2)时,对于任意的σ和r组合似乎都不会发生颤振。
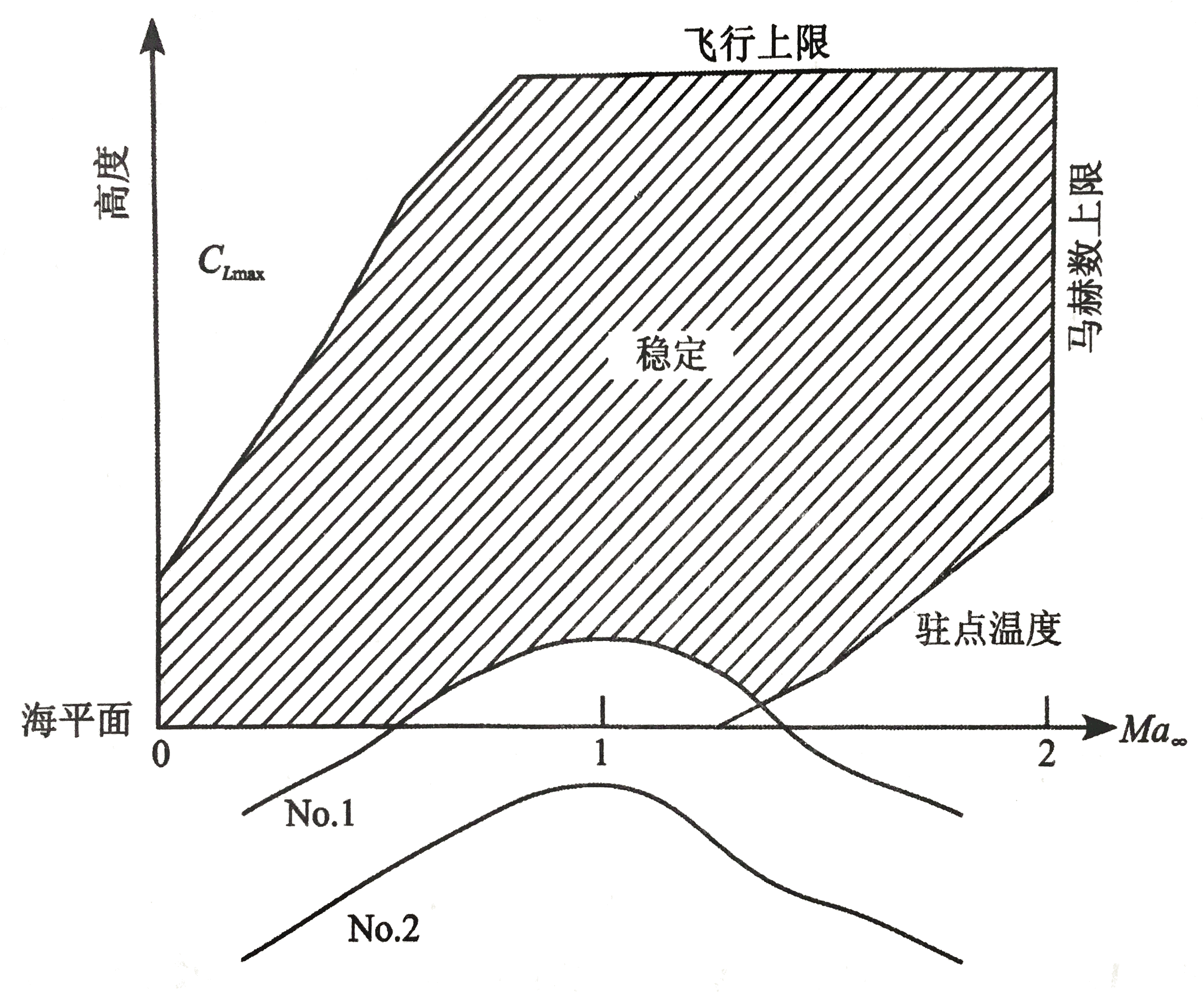
颤振边界一种可能的表示方式是与飞行包线一起给出。一架马赫数为2的攻击机的典型飞行包线如图所示:
图中记为No.1和No.2的曲线表示颤振边界。可以看出此飞行器容易发生颤振的条件:低高度,跨声速流,大动压。
9 总结
气动弹性颤振的分析方法有:p法、经典颤振分析方法、k法和p-k法。
本文章使用limfx的vsocde插件快速发布