复合材料结构力学涉猎（下）

5 层合板的弯曲、屈曲与振动方程
- 5.1 基本假设
- 5.2 基本方程
6 各向异性层合圆柱壳分析
7 复合材料层合结构有限元分析
8 总结

5 层合板的弯曲、屈曲与振动方程

由复合材料力学知，由于层合板厚度方向的非均质性，存在面内要素和弯曲要素的耦合效应。

5.1 基本假设

克希荷夫（Kirchhoff）的直法线假设，变形前垂直于层合板中面的一直线段，变形后仍作为直线段垂直于变形后的中曲面，且其长度保持不变。具体说，此假设意味着忽略了横向剪切变形及横向正应变影响，即： $γ_{y z} = γ_{x z} = ϵ_{z} = 0$ 。
每一单层可近似被认为处于平面应力状态。即： $σ_{z} = τ_{y z} = τ_{x z}$ 。但是，当平板有横向外载荷作用时， $τ_{y z}$ 和 $τ_{x z}$ 又是平衡所必须的。
小应变假设：应变量 $ϵ_{x}$ 、 $ϵ_{y}$ 和 $γ_{x y}$ 与1相比为一小量。于是几何方程为线性。

5.2 基本方程

5.2.1 弯曲方程

在层合板中取一正方形板微元，其受力如图所示：
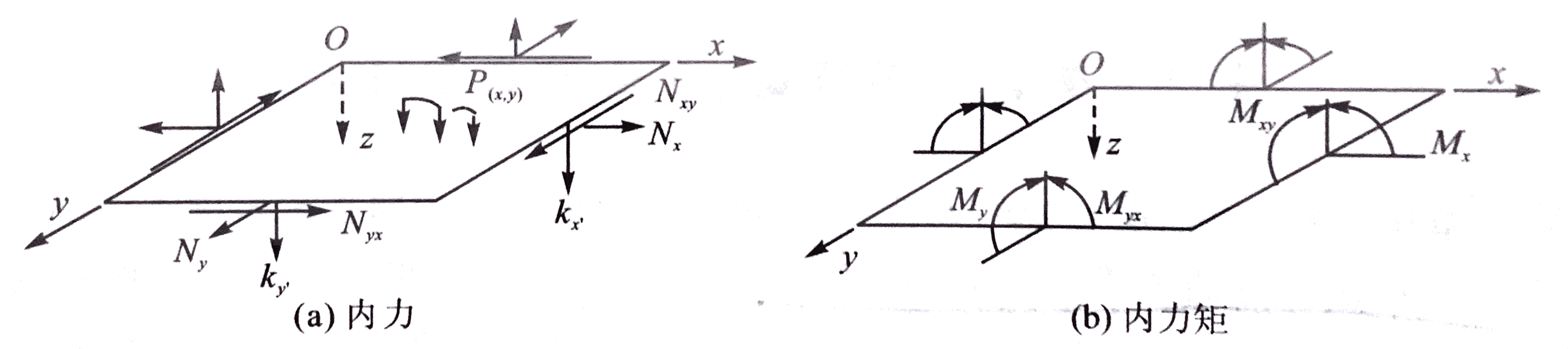
层合圆柱壳的坐标系及各个物理量
对于面内内力和内力矩，有平衡关系：

$\sum F_{x} = 0 : (N_{x} + \frac{\partial N _{x}}{\partial x} d x) - N_{x} + (N_{y x} + \frac{\partial N _{y x}}{\partial y} d y) - N_{y x} = 0 \sum F_{y} = 0 : (N_{y} + \frac{\partial N _{y}}{\partial y} d y) - N_{y} + (N_{x y} + \frac{\partial N _{x y}}{\partial x} d x) - N_{x y} = 0 \sum M_{z} = 0 : (N_{x y} + \frac{\partial N _{x y}}{\partial x} d x) \frac{d x}{2} + N_{x y} \frac{d x}{2} - (N_{y x} + \frac{\partial N _{y x}}{\partial y} d y) \frac{d y}{2} - N_{y x} \frac{d y}{2} = 0$

微元为正方形板微元： $d x = d y$ 。代入上式略去高阶量，化简得：

$\frac{\partial N _{x}}{\partial x} + \frac{\partial N _{y x}}{\partial y} = 0 \frac{\partial N _{x y}}{\partial x} + \frac{\partial N _{y}}{\partial y} = 0 N_{x y} = N_{y x}$

对于面外内力和内力矩：板单元图
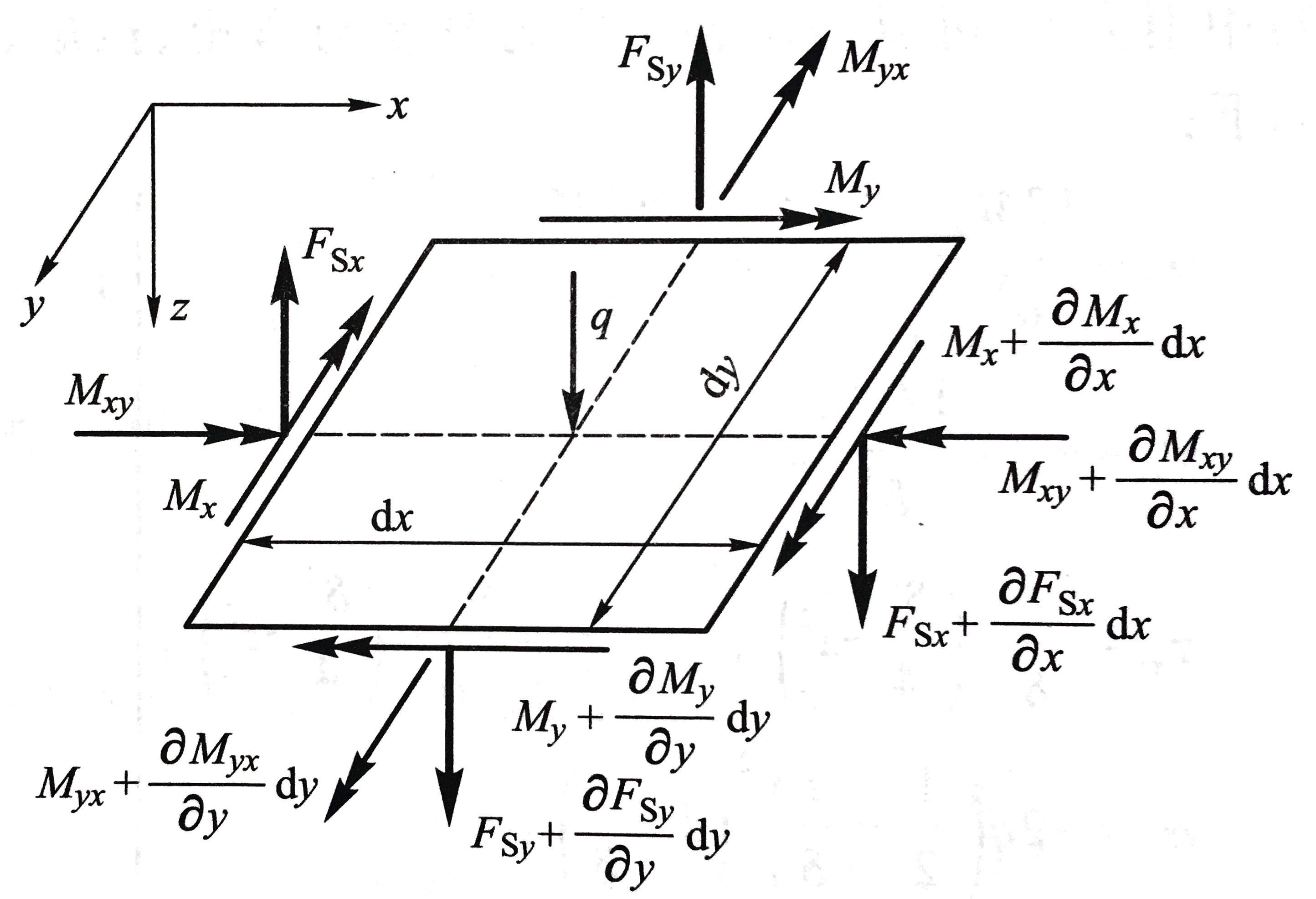
有平衡关系：

$\sum M_{x} = 0 ： M_{x y} - (M_{x y} + \frac{\partial M _{x y}}{\partial x} d x) + M_{y} - (M_{y} + \frac{\partial M _{y}}{\partial y} d y) + F_{S y} \frac{d y}{2} + (F_{S y} + \frac{\partial F _{S y}}{\partial y} d y) \frac{d y}{2} = 0 \sum M_{y} = 0 ： (M_{y x} + \frac{\partial M _{y x}}{\partial y} d y) - M_{y x} + (M_{x} + \frac{\partial M _{x}}{\partial x} d x) - M_{x} - F_{S x} \frac{d x}{2} + (F_{S x} + \frac{\partial F _{S x}}{\partial x} d x) \frac{d x}{2} = 0 \sum F_{z} = 0 : F_{S x} - (F_{S x} + \frac{\partial F _{S x}}{\partial x} d x) + F_{S y} - (F_{S y} + \frac{\partial F _{S y}}{\partial y} d y) - q = 0$

由剪切互等定理得： $τ_{x y} = τ_{y x}$ ，于是 $M_{x y} = \int_{- δ / 2}^{δ / 2} z τ_{x y} d z = \int_{- δ / 2}^{δ / 2} z τ_{y x} d z = M_{y x}$ 。又有 $d x = d y$ 。将二者代入上式，并略去高阶量，化简得：

$F_{S x} = \frac{\partial M _{x}}{\partial x} + \frac{\partial M _{y x}}{\partial y} F_{S y} = \frac{\partial M _{y}}{\partial y} + \frac{\partial M _{x y}}{\partial x} \frac{\partial ^{2} M _{x}}{\partial x ^{2}} + 2 \frac{\partial ^{2} M _{x y}}{\partial x \partial y} + \frac{\partial ^{2} M _{y}}{\partial y ^{2}} + q = 0$

综合面内和面外的平衡方程，得弯曲平衡方程：

$N_{x, x} + N_{x y, y} = 0 N_{x y, x} + N_{y, y} = 0 M_{x, x x} + 2 M_{x y, x y} + M_{y, y y} = - p ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫ (5.2.1.1)$

式中下标中的逗号“ $,$ ”表示各内力对下标变量的偏导。

由经典层合板理论得物理方程和几何方程（其中： $A_{i j} = A_{j i}, B_{i j} = B_{j i}, D_{i j} = D_{j i}$ ）：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ N_{x} N_{y} N_{x y} M_{x} M_{y} M_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ A_{11} A_{21} A_{61} B_{11} B_{21} B_{61} A_{12} A_{22} A_{62} B_{12} B_{22} B_{62} A_{16} A_{26} A_{66} B_{16} B_{26} B_{66} B_{11} B_{21} B_{61} D_{11} D_{21} D_{61} B_{12} B_{22} B_{62} D_{12} D_{22} D_{62} B_{16} B_{26} B_{66} D_{16} D_{26} D_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x}^{(0)} ϵ_{y}^{(0)} γ_{x y}^{(0)} κ_{x} κ_{y} κ_{x y} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ ϵ_{x}^{(0)} ϵ_{y}^{(0)} γ_{x y}^{(0)} ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ \frac{\partial u _{0}}{\partial x} \frac{\partial v _{0}}{\partial y} \frac{\partial u _{0}}{\partial y} + \frac{\partial v _{0}}{\partial x} ⎦ ⎥ ⎥ ⎤, ⎣ ⎢ ⎡ κ_{x} κ_{y} κ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ - \frac{\partial ^{2} w _{0}}{\partial x ^{2}} - \frac{\partial ^{2} w _{0}}{\partial y ^{2}} - 2 \frac{\partial ^{2} w _{0}}{\partial x \partial y} ⎦ ⎥ ⎥ ⎤$

位移法：
将各个内力化为用位移表示的形式，然后，依照公式进行求导并代入到 $(5.2.1.1)$ ，即可得到用位移分量表示的弯曲平衡方程（为了书写方便，以后将中面位移的零下标去掉）：

$A_{11} u_{, x x} + 2 A_{16} u_{, x y} + A_{66} u_{, y y} + A_{16} v_{, x x} + (A_{12} + A_{66}) v_{, x y} + A_{26} v_{, y y} - B_{11} w_{, x x x} - 3 B_{16} w_{, x x y} - (B_{12} + 2 B_{66}) w_{, x y y} - B_{26} w_{, y y y} = 0 A_{16} u_{, x x} + (A_{12} + A_{66}) u_{, x y} + A_{26} u_{, y y} + A_{66} v_{, x x} + 2 A_{26} v_{, x y} + A_{22} v_{, y y} - B_{16} w_{, x x x} - (B_{12} + 2 B_{66}) w_{, x x y} - 3 B_{26} w_{, x y y} - B_{22} w_{, y y y} = 0 D_{11} w_{, x x x x} + 4 D_{16} w_{, x x x y} + 2 (D_{12} + 2 D_{66}) w_{, x x y y} + 4 D_{26} w_{x y y y} + D_{22} w_{, y y y y} - B_{11} u_{, x x x} - 3 B_{16} u_{, x x y} - (B_{12} + 2 B_{66}) u_{, x y y} - B_{26} u_{y y y} - B_{16} v_{, x x x} - (B_{12} + 2 B_{66}) v_{, x x y} - 3 B_{26} v_{, x y y} - B_{22} v_{, y y y} = p ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

若定义微分算子：

$L_{11} = A_{11} \frac{\partial ^{2}}{\partial x ^{2}} + 2 A_{16} \frac{\partial ^{2}}{\partial x \partial y} + A_{66} \frac{\partial ^{2}}{\partial y ^{2}} L_{12} = A_{16} \frac{\partial ^{2}}{\partial x ^{2}} + (A_{12} + A_{66}) \frac{\partial ^{2}}{\partial x \partial y} + A_{26} \frac{\partial ^{2}}{\partial y ^{2}} L_{22} = A_{66} \frac{\partial ^{2}}{\partial x ^{2}} + 2 A_{26} \frac{\partial ^{2}}{\partial x \partial y} + A_{22} \frac{\partial ^{2}}{\partial y ^{2}} L_{13} = - [B_{11} \frac{\partial ^{3}}{\partial x ^{3}} + 3 B_{16} \frac{\partial ^{3}}{\partial x ^{2} \partial y} + (B_{12} + 2 B_{66}) \frac{\partial ^{3}}{\partial x \partial y ^{2}} + B_{26} \frac{\partial ^{3}}{\partial y ^{3}}] L_{23} = - [B_{16} \frac{\partial ^{3}}{\partial x ^{3}} + (B_{12} + 2 B_{66}) \frac{\partial ^{3}}{\partial x ^{2} \partial y} + 3 B_{26} \frac{\partial ^{3}}{\partial x \partial y ^{2}} + B_{22} \frac{\partial ^{3}}{\partial y ^{3}}] L_{33} = D_{11} \frac{\partial ^{4}}{\partial x ^{4}} + 4 D_{16} \frac{\partial ^{4}}{\partial x ^{3} \partial y} + 2 (D_{12} + 2 D_{66}) \frac{\partial ^{4}}{\partial x ^{2} \partial y ^{2}} + 4 D_{26} \frac{\partial ^{4}}{\partial x \partial y ^{3}} + D_{22} \frac{\partial ^{4}}{\partial y ^{4}} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

则弯曲方程可写作：

$⎣ ⎢ ⎡ L_{11} L_{21} L_{31} L_{12} L_{22} L_{32} L_{13} L_{23} L_{33} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ u v w ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 00 p ⎦ ⎥ ⎤ (5.2.1.2)$

从上面的方程可以看出对于一般的层合板来说，有三类耦合效应。
1. 第一类耦合效应被称为泊松效应。可由 $A_{12}$ 体现： $x$ 和 $y$ 方向的轴力 $N_{x}$ 和 $N_{y}$ 会分别影响对方方向的正应变 $ϵ_{y}$ 和 $ϵ_{x}$ ；也可由 $D_{12}$ 体现： $x$ 和 $y$ 方向的弯矩 $M_{x}$ 和 $M_{y}$ 会分别影响对方方向的曲率 $κ_{y}$ 和 $κ_{x}$ 。这种耦合效应在各向同性材料中也存在。
2. 第二类耦合效应被称为交叉效应。可由 $A_{16}$ 或 $A_{26}$ 体现：轴力（ $N_{x}$ 或 $N_{y}$ ）和剪力（ $N_{x y}$ ）会影响对方方向上的应变（ $γ_{x y}$ 与 $ϵ_{x}$ 或 $ϵ_{y}$ ）；也可由 $D_{16}$ 或 $D_{26}$ 体现：弯矩（ $M_{x}$ 或 $M_{y}$ ）和扭矩（ $M_{x y}$ ）会影响对方方向上的扭率曲率（ $κ_{x y}$ 与 $κ_{x}$ 或 $κ_{y}$ ）。这种耦合效应在非正交非反对称的层合板中存在。它是由层合板各向异性特性引起的，故在普通的均质各向异性材料中也存在。
3. 第三类耦合效应被称为复杂耦合效应。可由 $B_{i j}$ 体现：面内作用力（ $N_{x}$ 、 $N_{y}$ 和 $N_{x y}$ ）和面外作用力（ $M_{x}$ 、 $M_{y}$ 和 $M_{x y}$ ）会影响对方方向上的变形，即面外曲率或扭率（ $κ_{x}$ 、 $κ_{y}$ 和 $κ_{x y}$ ）与面内应变（ $ϵ_{x}$ 、 $ϵ_{y}$ 和 $γ_{x y}$ ）。这种耦合效应存在于非对称层合板中。它是由层合板厚度方向的非均质性引起的。
要求解上述方程，还需要确定边界条件。通常的边界条件为简支、固支和自由边界三种。

简支边界条件（用字母 $S$ 表示）和固支边界条件（用字母 $C$ 表示）分成四种类型设 $n$ 为边界外法线方向， $t$ 为边界切线方向。则二者可写成：

$S 1 : S 2 : S 3 : S 4 : w = 0 w = 0 w = 0 w = 0 M_{n} = 0 M_{n} = 0 M_{n} = 0 M_{n} = 0 u_{n} = \overline{u}_{n} N_{n} = \overline{N}_{n} u_{n} = \overline{u}_{n} N_{n} = \overline{N}_{n} u_{t} = \overline{u}_{t} u_{t} = \overline{u}_{t} N_{n t} = \overline{N}_{n t} N_{n t} = \overline{N}_{n t} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫ (5.2.1.3)$

$C 1 : C 2 : C 3 : C 4 : w = 0 w = 0 w = 0 w = 0 M_{, n} = 0 M_{, n} = 0 M_{, n} = 0 M_{, n} = 0 u_{n} = \overline{u}_{n} N_{n} = \overline{N}_{n} u_{n} = \overline{u}_{n} N_{n} = \overline{N}_{n} u_{t} = \overline{u}_{t} u_{t} = \overline{u}_{t} N_{n t} = \overline{N}_{n t} N_{n t} = \overline{N}_{n t} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫ (5.2.1.4)$

带定标“-”的量为一定值，他们常常为零值。
力法：
力法是以应力函数 $F (x, y)$ 和挠度 $w$ 为基本未知量，其弯曲控制方程为：

$[L_{f F} L_{w F} L_{w F} F_{w w}] [F w] = [0 p] (5.2.1.5)$

上面方程结合内力形式的边界条件求解出应力函数 $F$ 和挠度函数 $w$ ，由下式求得各内力和各曲率：

$N_{x} = \frac{\partial ^{2} F}{\partial y ^{2}}, N_{y} = \frac{\partial ^{2} F}{\partial x ^{2}}, N_{x y} = - \frac{\partial ^{2} F}{\partial x \partial y} κ_{x} = - \frac{\partial ^{2} w}{\partial x ^{2}}, κ_{y} = - \frac{\partial ^{2} w}{\partial y ^{2}}, κ_{x y} = - \frac{\partial ^{2} w}{\partial x \partial y}$

再根据层合板半逆形式得物理方程：

$[ϵ^{0} M] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ a \dots c ⋮ ⋮ ⋮ b \dots d ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ [N κ]$

进一步求得中面应变和弯曲力矩。

5.2.2 屈曲方程

如图所示，当层合板再面内承受压缩载荷和剪切载荷，且载荷达到一定数值时，层合板即开始偏离原来的稳定状态而发生屈曲，通常称此载荷为屈曲载荷。与各向同性平板截然不同得是，由于层合平板带来的耦合效应，在达到屈曲载荷值之前，即使处在稳定平衡状态，板也会产生挠曲变形而有一初始挠度存在，这样，就使屈曲问题得求解变得更复杂了。为了简化分析，在此不考虑耦合效应引起的初始挠度对屈曲得影响。
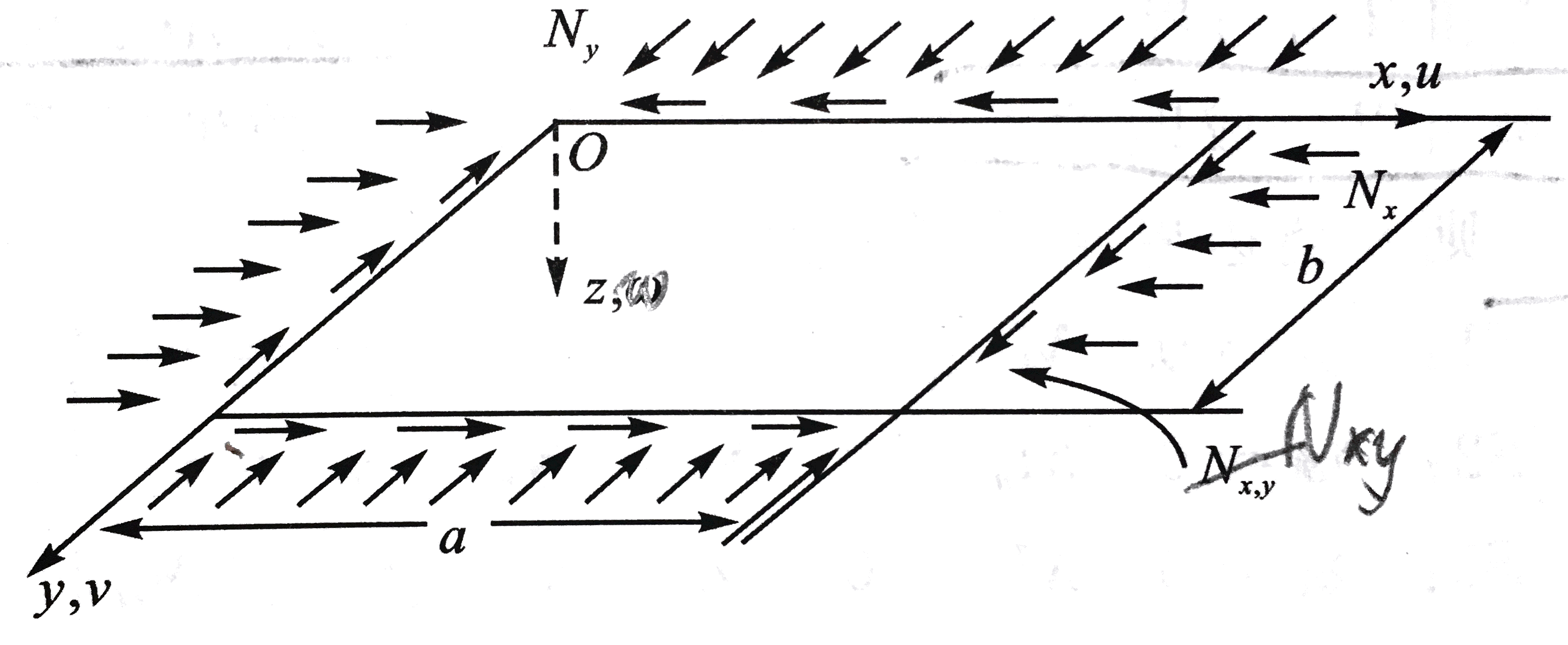
曲边四边形的实际单元

如果用 $δ$ 表示为临界状态附近的变分，则相应的各种关系式可写为几何方程得：

$[δ ϵ^{0}] = ⎣ ⎢ ⎡ δ ϵ_{x}^{0} δ ϵ_{y}^{0} δ γ_{x y}^{0} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ δ u_{, x} δ v_{, y} δ u_{, y} + δ v_{, x} ⎦ ⎥ ⎤ [δ κ] = ⎣ ⎢ ⎡ δ κ_{x} δ κ_{y} δ κ_{x y} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ - δ w_{, x x} - δ w_{, y y} - 2 δ w_{, x y} ⎦ ⎥ ⎤ ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (5.2.2.1)$

写为物理方程得：

$[δ N δ M] = [A B B D] [δ ϵ^{0} δ κ] (5.2.2.2)$

其中：

偏离状态的平衡条件得：

$δ N_{x, x} + δ N_{x y, y} = 0 δ N_{x y, x} + δ N_{y, y} = 0 δ M_{x, x x} + 2 δ M_{x y, x y} + δ M_{y, y y} + \overline{N}_{x} δ w_{, x x} + 2 \overline{N}_{x y} δ w_{, x y} + \overline{N}_{y} δ w_{, y y} = 0 ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫ (5.2.2.3)$

其中， $\overline{N}_{x}$ 、 $\overline{N}_{y}$ 和 $\overline{N}_{x y}$ 为横向载荷 $p$ 的分量。

与推导弯曲平衡方程类似，将 $(5.2.2.1)$ 代入到 $(5.2.2.2)$ ，再代入到 $(5.2.2.3)$ 得：

$A_{11} δ u_{, x x} + 2 A_{16} δ u_{, x y} + A_{66} δ u_{, y y} + A_{16} δ v_{, x x} + (A_{12} + A_{66}) δ v_{, x y} + A_{26} δ v_{, y y} - B_{11} δ w_{, x x x} - 3 B_{16} δ w_{, x x y} - (B_{12} + 2 B_{66}) δ w_{, x y y} - B_{26} δ w_{, y y y} = 0 A_{16} δ u_{, x x} + (A_{12} + A_{66}) δ u_{, x y} + A_{26} δ u_{, y y} + A_{66} δ v_{, x x} + 2 A_{26} δ v_{, x y} + A_{22} δ v_{, y y} - B_{16} δ w_{, x x x} - (B_{12} + 2 B_{66}) δ w_{, x x y} - 3 B_{26} δ w_{, x y y} - B_{22} δ w_{, y y y} = 0 D_{11} δ w_{, x x x x} + 4 D_{16} δ w_{, x x x y} + 2 (D_{12} + 2 D_{66}) δ w_{, x x y y} + 4 D_{26} δ w_{x y y y} + D_{22} δ w_{, y y y y} - B_{11} δ u_{, x x x} - 3 B_{16} δ u_{, x x y} - (B_{12} + 2 B_{66}) δ u_{, x y y} - B_{26} δ u_{y y y} - B_{16} δ v_{, x x x} - (B_{12} + 2 B_{66}) δ v_{, x x y} - 3 B_{26} δ v_{, x y y} - B_{22} δ v_{, y y y} = p ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

同样可简写为：

$⎣ ⎢ ⎡ L_{11} L_{21} L_{31} L_{12} L_{22} L_{32} L_{13} L_{23} L_{33} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ δ u δ v δ w ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 00 \overline{N}_{x} δ w_{, x x} + 2 \overline{N}_{x y} δ w_{, x y} + \overline{N}_{y} δ w_{, y y} ⎦ ⎥ ⎤ (5.2.2.4)$

边界条件可表示为：

$S 1 : S 2 : S 3 : S 4 : δ w = 0 δ w = 0 δ w = 0 δ w = 0 δ M_{n} = 0 δ M_{n} = 0 δ M_{n} = 0 δ M_{n} = 0 δ u_{n} = \overline{δ u}_{n} N_{n} = \overline{N}_{n} δ u_{n} = \overline{δ u}_{n} N_{n} = \overline{N}_{n} δ u_{t} = \overline{δ u}_{t} δ u_{t} = \overline{δ u}_{t} N_{n t} = \overline{N}_{n t} N_{n t} = \overline{N}_{n t} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫ (5.2.2.5)$

$C 1 : C 2 : C 3 : C 4 : δ w = 0 δ w = 0 δ w = 0 δ w = 0 δ M_{, n} = 0 δ M_{, n} = 0 δ M_{, n} = 0 δ M_{, n} = 0 δ u_{n} = 0 N_{n} = 0 δ u_{n} = 0 N_{n} = 0 δ u_{t} = 0 δ u_{t} = 0 N_{n t} = 0 N_{n t} = 0 ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫ (5.2.2.6)$

可以看出弯曲方程和屈曲方程很相似。然而它们在本质上时完全不同的，前者在数学上是边界值问题；后者在数学上是特征值问题，其本质是求引起屈曲的最小外载荷 $\overline{N}_{i j}$ 的大小，而屈曲后的变形使不能确定的。

5.2.3 振动方程

层合板的振动或对于静平衡状态下的振荡，如同板的屈曲一样，也是一个特征值问题，其目的是确定层合板振动时的自振频率 $ω$ 和振型。所讨论的问题只限于横向振动的范畴，并忽略了转动惯量的影响（因为对于低频振动和长波振动，它的纵向和横向惯性相比为一小量。而在中频和高频振动中就必须考虑它的影响）。

其几何方程与物理方程和屈曲变形完全相同，振动方程可写为：

$δ N_{x, x} + δ N_{x y, y} = 0 δ N_{x y, x} + δ N_{y, y} = 0 δ M_{x, x x} + 2 δ M_{x y, x y} + δ M_{y, y y} = ρ δ w_{, t t} ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫ (5.2.3.1)$

式中， $ρ$ 为层合板密度， $t$ 为时间坐标变量。

于是振动方程可写为：

$⎣ ⎢ ⎡ L_{11} L_{21} L_{31} L_{12} L_{22} L_{32} L_{13} L_{23} L_{33} ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ δ u δ v δ w ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 00 - ρ δ w_{, t t} ⎦ ⎥ ⎤ (5.2.3.2)$

其边界条件与屈曲问题一样。

6 各向异性层合圆柱壳分析

与层合平板弯曲不同，层合壳中面法线变形后虽然也为直线，但它不再垂直于壳体中面，而是从它的垂直位置存在一个横向剪应变限定的角应变。考虑了横向剪切变形沿壳体壁厚的平均效应。

6.1 基本方程式

由弹性力学知识知：在正交曲线坐标系中，几何方程写作：

$e_{1} = \frac{1}{H _{1}} \frac{\partial u _{1}}{\partial α} + \frac{1}{H _{1} H _{2}} \frac{\partial H _{1}}{\partial β} u_{2} + \frac{1}{H _{1} H _{3}} \frac{\partial H _{1}}{\partial γ} u_{3} e_{2} = \frac{1}{H _{2}} \frac{\partial u _{2}}{\partial α} + \frac{1}{H _{2} H _{3}} \frac{\partial H _{2}}{\partial β} u_{3} + \frac{1}{H _{2} H _{1}} \frac{\partial H _{2}}{\partial γ} u_{1} e_{3} = \frac{1}{H _{3}} \frac{\partial u _{3}}{\partial α} + \frac{1}{H _{3} H _{1}} \frac{\partial H _{3}}{\partial β} u_{1} + \frac{1}{H _{3} H _{2}} \frac{\partial H _{3}}{\partial γ} u_{2} e_{23} = \frac{H _{3}}{H _{2}} \frac{\partial}{\partial β} (\frac{u _{3}}{H _{3}}) + \frac{H _{2}}{H _{3}} \frac{\partial}{\partial γ} (\frac{u _{2}}{H _{2}}) e_{31} = \frac{H _{1}}{H _{3}} \frac{\partial}{\partial γ} (\frac{u _{1}}{H _{1}}) + \frac{H _{3}}{H _{1}} \frac{\partial}{\partial α} (\frac{u _{3}}{H _{3}}) e_{12} = \frac{H _{2}}{H _{1}} \frac{\partial}{\partial α} (\frac{u _{2}}{H _{2}}) + \frac{H _{1}}{H _{2}} \frac{\partial}{\partial β} (\frac{u _{1}}{H _{1}}) ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (6.1.1)$

其中， $e$ 表示应变； $α$ 、 $β$ 和 $γ$ 是曲线坐标； $u_{1}$ 、 $u_{2}$ 和 $u_{3}$ 是对应曲线坐标方向的位移； $H_{1}$ 、 $H_{2}$ 和 $H_{3}$ 为拉梅系数，表示在曲线坐标系中，从某一点沿 $α$ 、 $β$ 或 $γ$ 方向延申的曲线长度与其在坐标轴上投影的长度的比值，即： $d s_{1} = H_{1} d α$ 。

如图所示，对于如图坐标系下的壳体，
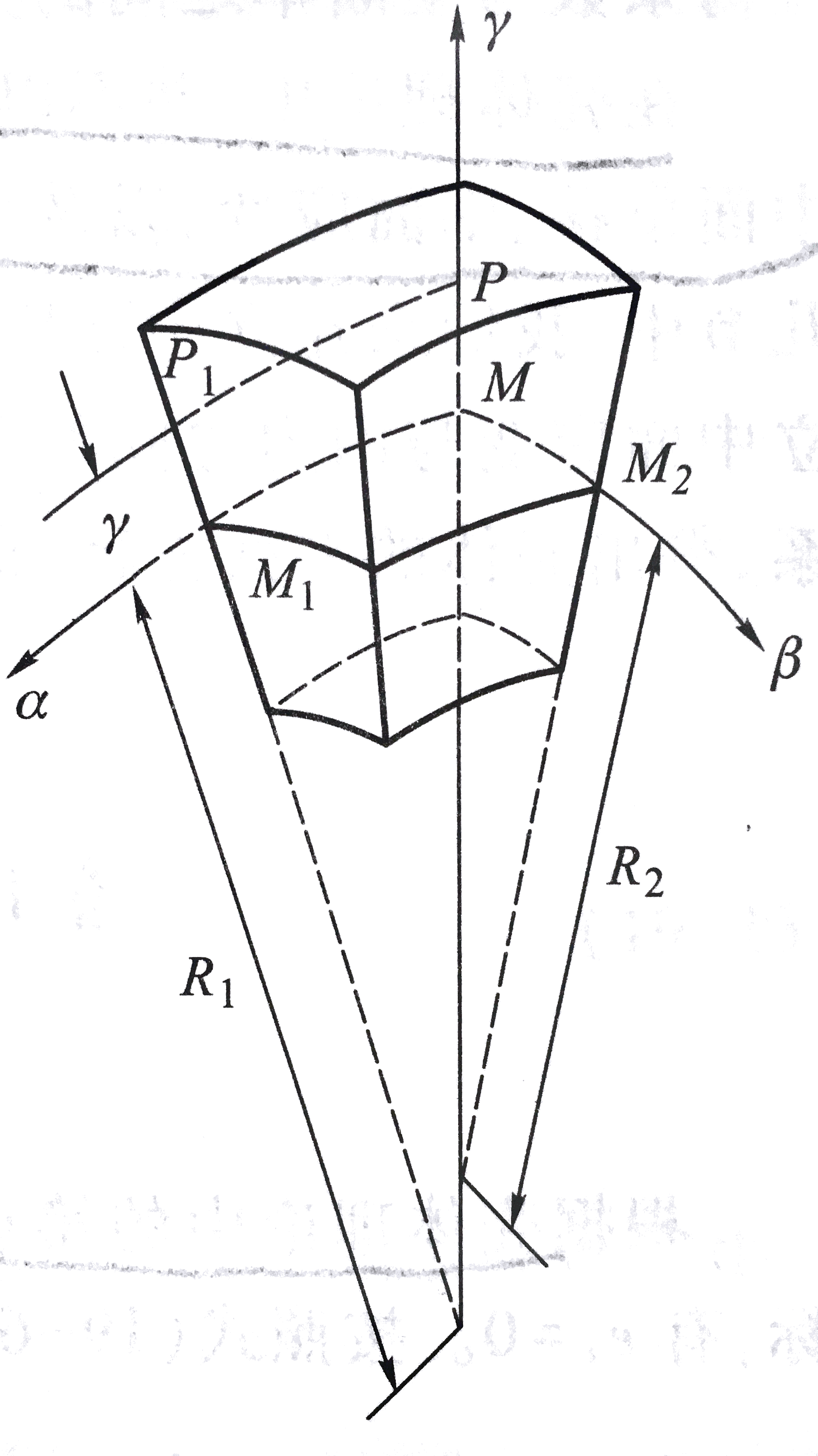
曲边四边形的实际单元
拉梅系数表示为：

$H_{1} = A (1 + κ_{1} γ) H_{2} = B (1 + κ_{2} γ) H_{3} = 1 ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫ (6.1.2)$

其中 $κ_{1} = 1 / R_{1}$ 为中面沿 $α$ 方向的主曲率， $κ_{2} = 1 / R_{2}$ 为中面沿 $β$ 方向的主曲率； $A$ 、 $B$ 为壳体中面处的拉梅系数： $A = (H_{1})_{γ = 0}, B = (H_{2})_{γ = 0}$ 。注意 $κ_{1}$ 、 $κ_{2}$ 、 $A$ 和 $B$ 都只是 $α$ 和 $β$ 的函数。

根据假设，中面的法线变形后仍为直线且保持长度不变：

$e_{23} = e_{23} (α, β) e_{31} = e_{31} (α, β) e_{3} = 0 ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫ (6.1.3)$

将上式中的第三式和 $(6.1.2)$ 代入 $(6.1.1)$ 第三式，得：

$\frac{\partial u _{3}}{\partial γ} = 0$

于是：

$u_{3} = u_{3} (α, β) = w (6.1.4)$

将上式、 $(6.1.3)$ 的前两式以及 $(6.1.2)$ 代入到 $(6.1.1)$ 得第四、五式得：

$\frac{\partial}{\partial γ} [\frac{u _{2}}{B ( 1 + κ _{2} γ )}] + \frac{1}{B ^{2} ( 1 + κ _{2} γ ) ^{2}} \frac{\partial w}{\partial β} = e_{23} (α, β) \frac{\partial}{\partial γ} [\frac{u _{1}}{A ( 1 + κ _{1} γ )}] + \frac{1}{A ^{2} ( 1 + κ _{1} γ ) ^{2}} \frac{\partial w}{\partial α} = e_{31} (α, β)$

将上面两式对 $γ$ 在 $0$ 到 $γ$ 上积分，并令 $(u_{1})_{γ = 0} = u_{0}$ ， $(u_{2})_{γ = 0} = v_{0}$ 得：

$[\frac{u _{1}}{A ( 1 + κ _{1} γ )} - \frac{u _{0}}{A}] - [\frac{1}{A ^{2} κ _{1} ( 1 + κ _{1} γ )} - \frac{1}{A ^{2} κ _{1}}] \frac{\partial w}{\partial α} = e_{31} γ [\frac{u _{2}}{B ( 1 + κ _{2} γ )} - \frac{v _{0}}{B}] - [\frac{1}{B ^{2} κ _{2} ( 1 + κ _{2} γ )} - \frac{1}{B ^{2} κ _{2}}] \frac{\partial w}{\partial β} = e_{23} γ$

化简联立 $(6.1.4)$ 得：

$u_{1} = u_{0} - γ (\frac{1}{A} \frac{\partial w}{\partial α} + A e_{31} - κ_{1} u_{0}) - γ^{2} A κ_{1} e_{31} u_{2} = v_{0} - γ (\frac{1}{B} \frac{\partial w}{\partial β} + B e_{23} - κ_{2} v_{0}) - γ^{2} B κ_{2} e_{23} u_{3} = w ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (6.1.5)$

上面将位移函数用中面位移和中面曲率改变量表示了出来。

下面研究特殊的圆柱壳，建立如图所示的层合圆柱壳的坐标系：
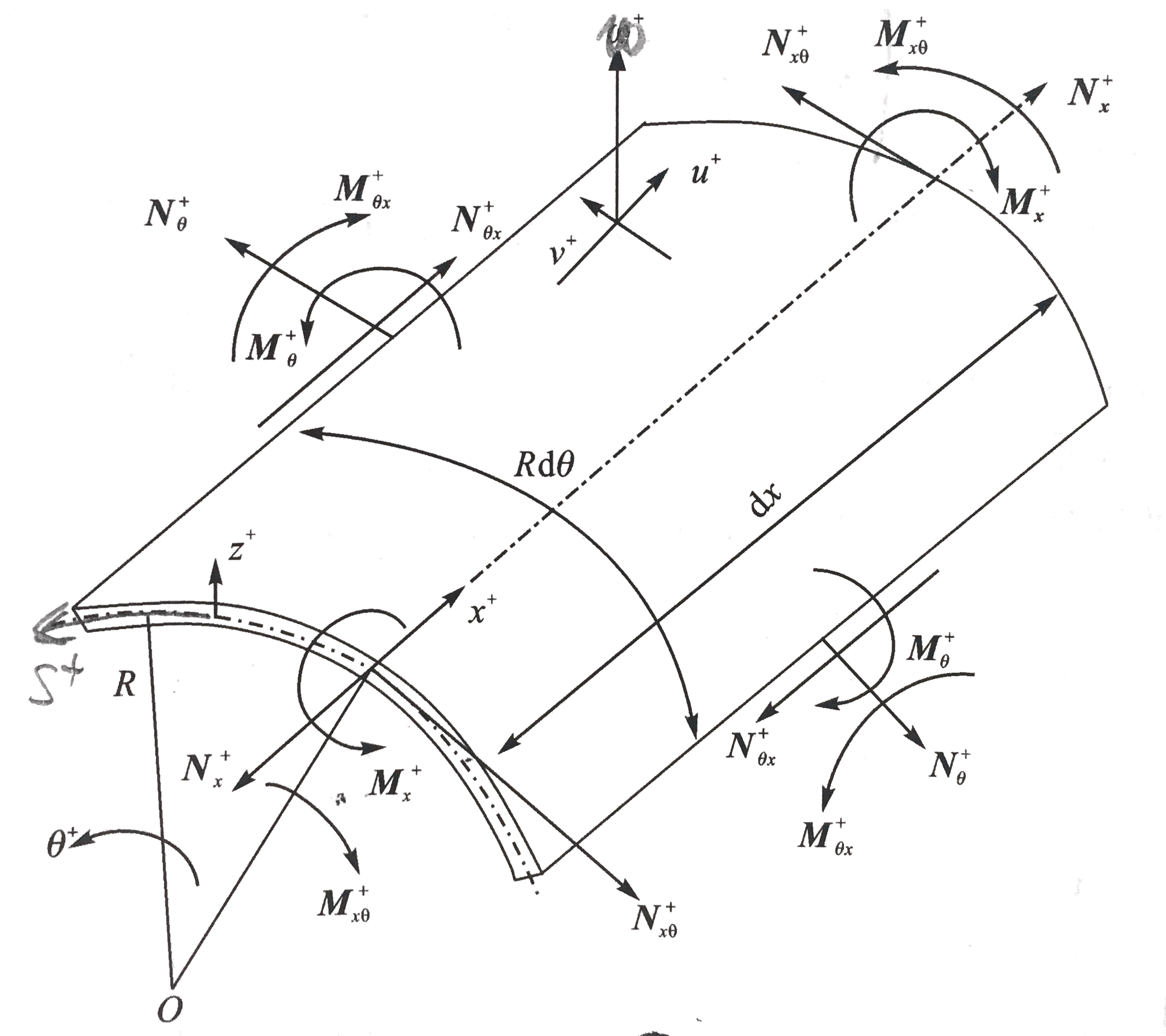
正方形基本单元

书中将 $(6.1.5)$ 式做了简化略去了 $γ$ 的二次项：

$u (x, θ, z) = u_{0} (x, θ) + z α (x, θ) v (x, θ, z) = v_{0} (x, θ) + z β (x, θ) w (x, θ, z) = w (x, θ) ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫$

其中， $u_{0}$ 、 $v_{0}$ 和 $w$ 分别为壳体中面沿 $x$ 、 $s$ 和 $z$ 方向的位移分量， $α$ 和 $β$ 分别为壳体中面法线沿 $x$ 和 $s$ 方向的转动分量。 $s = R θ$ 。

将上式代入到 $(6.1.1)$ 中，并注意到此时 $H_{1} = H_{3} = 1, H_{2} = 1 + z / R$ ， $(6.1.1)$ 中的 $α$ 、 $β$ 和 $γ$ 分别对应上式中的 $x$ 、 $θ$ 和 $z$ ，不要将上式中的 $α (x, θ)$ 、 $β (x, θ)$ 与 $(6.1.1)$ 中的 $α$ 和 $β$ 相混淆。得：

$ϵ_{x}^{0} = \frac{\partial u _{0}}{\partial x} ϵ_{θ}^{0} = \frac{\partial v _{0}}{\partial s} + \frac{w}{R} γ_{x θ}^{0} = \frac{\partial v _{0}}{\partial x} + \frac{\partial u _{0}}{\partial s} κ_{x} = \frac{\partial α}{\partial x} κ_{y} = \frac{\partial β}{\partial y} κ_{x θ} = \frac{\partial α}{\partial s} + \frac{\partial β}{\partial x} γ_{x z} = α + \frac{\partial w}{\partial x} γ_{θ z} = β + \frac{\partial w}{\partial s} - \frac{v _{0}}{R} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

或改写为矩阵形式的几何方程：

$ϵ^{0} = ⎣ ⎢ ⎡ ϵ_{x}^{0} ϵ_{θ}^{0} γ_{x θ}^{0} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ u_{0, x} v_{0, s} + \frac{w}{R} v_{0, x} + u_{0, s} ⎦ ⎥ ⎤ (6.1.6)$

$κ = ⎣ ⎢ ⎡ κ_{x} κ_{y} κ_{x θ} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ α_{, x} β_{, s} α_{, s} + β_{, x} ⎦ ⎥ ⎤ (6.1.7)$

$γ = [γ_{x z} γ_{θ z}] = [α + w_{, x} β + w_{, s} - \frac{v _{0}}{R}] (6.1.8)$

$ϵ = ⎣ ⎢ ⎡ ϵ_{x} ϵ_{θ} γ_{x θ} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ ϵ_{x}^{0} ϵ_{θ}^{0} γ_{x θ}^{0} ⎦ ⎥ ⎤ + z ⎣ ⎢ ⎡ κ_{x} κ_{y} κ_{x θ} ⎦ ⎥ ⎤ = ϵ^{0} + z κ$

其中， $ϵ^{0}$ 表示中面面内应变； $κ$ 表示中面曲率改变量； $γ$ 表示横向剪切应变； $ϵ$ 表示面内应变。

层合圆柱壳的物理方程式与层合平板的物理方程式相似：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ N_{x} N_{θ} N_{x θ} M_{x} M_{θ} M_{x θ} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ A_{11} A_{21} A_{61} B_{11} B_{21} B_{61} A_{12} A_{22} A_{62} B_{12} B_{22} B_{62} A_{16} A_{26} A_{66} B_{16} B_{26} B_{66} B_{11} B_{21} B_{61} D_{11} D_{21} D_{61} B_{12} B_{22} B_{62} D_{12} D_{22} D_{62} B_{16} B_{26} B_{66} D_{16} D_{26} D_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x}^{0} ϵ_{θ}^{0} γ_{x θ}^{0} κ_{x} κ_{θ} κ_{x θ} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ (6.1.9)$

以及

$[Q_{x z} Q_{θ z}] = [A_{55} A_{45} A_{45} A_{44}] [γ_{x z} γ_{θ z}] (6.1.10)$

其中：

$A_{i j} = k = 1 \sum N \overline{Q}_{i j}^{(k)} (z_{k + 1} - z_{k}) B_{i j} = \frac{1}{2} k = 1 \sum N \overline{Q}_{i j}^{(k)} (z_{k + 1}^{2} - z_{k}^{2}) D_{i j} = \frac{1}{3} k = 1 \sum N \overline{Q}_{i j}^{(k)} (z_{k + 1}^{3} - z_{k}^{3}) ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (i, j = 1, 2, 3, 4, 5, 6) A_{i j} = \frac{5}{4} k = 1 \sum n C_{i j}^{(k)} [h_{k} - h_{k - 1} - \frac{4}{3} \frac{h _{k}^{3} - h _{k - 1}^{3}}{h ^{2}}] (i, j = 4, 5)$

圆柱壳的平衡方程：

$N_{x, x} + N_{x θ, s} = - q_{x} + \overline{ρ} u_{0, t t} + H_{α, t t} N_{x θ, x} + N_{θ, x} + \frac{Q _{θ z}}{R} = - q_{θ} + \overline{ρ} v_{0, t t} + H β_{, t t} Q_{x z, x} + Q_{θ z, s} - \frac{N _{θ}}{R} = - p (x, θ) + \overline{ρ} w_{, t t} M_{x, x} + M_{x θ, s} - Q_{x z} = - m_{x} + J α_{, t t} + H u_{0, t t} M_{θ x, x} + M_{θ, s} - Q_{θ z} = - m_{θ} + J β_{, t t} + H v_{0, t t} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

其中：

$⎣ ⎢ ⎡ N_{x} N_{θ} N_{x θ} ⎦ ⎥ ⎤ = k = 1 \sum n \int_{z_{k}}^{z_{k + 1}} ⎣ ⎢ ⎡ σ_{x} σ_{θ} τ_{x θ} ⎦ ⎥ ⎤ d z ⎣ ⎢ ⎡ M_{x} M_{θ} M_{x θ} ⎦ ⎥ ⎤ = k = 1 \sum n \int_{z_{k}}^{z_{k + 1}} ⎣ ⎢ ⎡ σ_{x} σ_{θ} τ_{x θ} ⎦ ⎥ ⎤ z d z [Q_{x z} Q_{θ z}] = k = 1 \sum n \int_{z_{k}}^{z_{k + 1}} [τ_{x z} τ_{θ z}] d z ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ q_{x} = τ_{x z} ∣_{- h / 2}^{h / 2} q_{θ} = τ_{θ z} ∣_{- h / 2}^{h / 2} m_{x} = z τ_{x z} ∣_{- h / 2}^{h / 2} m_{θ} = z τ_{θ z} ∣_{- h / 2}^{h / 2} p = σ_{z} ∣_{- h / 2}^{h / 2} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ \overline{ρ} = k = 1 \sum n ρ_{0}^{(k)} (z_{k + 1} - z_{k}) H = \frac{1}{2} k = 1 \sum n ρ_{0}^{(k)} (z_{k + 1}^{2} - z_{k}^{2}) J = \frac{1}{3} k = 1 \sum n ρ_{0}^{(k)} (z_{k + 1}^{3} - z_{k}^{3}) ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

采用位移法求解弹性力学基本方程时，将物理方程借助于几何方程均化为用位移表示的函数式，然后根据基本平衡方程的需要进行求导并综合，最后得到以位移形式表示的平衡方程。

当考虑单纯研究层合圆柱壳体的自由振动问题时，则令原式中的各种外载荷项为零，即：

$q_{x} = q_{θ} = m_{x} = m_{θ} = p = 0$

得到此时的位移形式表示的平衡方程：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ L_{11} L_{21} L_{31} L_{41} L_{51} L_{12} L_{22} L_{32} L_{42} L_{52} L_{13} L_{23} L_{33} L_{43} L_{53} L_{14} L_{24} L_{34} L_{44} L_{54} L_{15} L_{25} L_{35} L_{45} L_{55} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u_{0} v_{0} α β w ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{ρ} 0 H 00 0 \overline{ρ} 0 H 0 H 0 J 00 0 H 0 J 0 0000 - \overline{ρ} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ \frac{\partial ^{2}}{\partial t ^{2}} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u_{0} v_{0} α β w ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ (6.1.11)$

如果又不计伸缩运动与转动运动之间的耦合影响，则 $H = 0$ ，这时基本方程可简洁地写为：

$L u = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{ρ} \overline{ρ} J J - \overline{ρ} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ \frac{\partial ^{2}}{\partial t ^{2}} u$

其中微分算子为：

$L_{11} = A_{11} ()_{, x x} + 2 A_{16} ()_{, s x} + A_{66} ()_{, s s} L_{12} = L_{21} = A_{16} ()_{, x x} + (A_{12} + A_{66}) ()_{, s x} + A_{26} ()_{, s s} L_{13} = L_{31} = B_{11} ()_{, x x} + 2 B_{16} ()_{, s x} + B_{66} ()_{, s s} L_{14} = L_{41} = B_{16} ()_{, x x} + (B_{12} + B_{66}) ()_{, s x} + B_{26} ()_{, s s} L_{15} = L_{51} = R^{- 1} [A_{12} ()_{, x} + A_{26} ()_{, s}] L_{22} = A_{66} ()_{, x x} + 2 A_{26} ()_{, s x} + A_{22} ()_{, s s} + A_{44} R^{- 2} () L_{23} = L_{32} = B_{16} ()_{, x x} + (B_{12} + B_{66}) ()_{, s x} + B_{26} ()_{, s s} + A_{45} R^{- 1} () L_{24} = L_{42} = B_{66} ()_{, x x} + 2 B_{26} ()_{, s x} + B_{22} ()_{, s s} + B_{44} R^{- 2} () L_{25} = L_{52} = R^{- 1} [(A_{26} + A_{45}) ()_{, x} + (A_{22} + A_{44}) ()_{, s})] L_{33} = D_{11} ()_{, x x} + 2 D_{16} ()_{, s x} + D_{66} ()_{, s x} - A_{55} () L_{34} = L_{43} = D_{16} ()_{, x x} + (D_{12} + D_{66}) ()_{, s x} + D_{26} ()_{, s s} - A_{45} () L_{35} = L_{53} = (B_{12} R^{- 1} - A_{55}) ()_{, x} + (B_{26} R^{- 1} - A_{45}) ()_{, s} L_{44} = D_{66} ()_{, x x} + 2 D_{26} ()_{, s x} + D_{22} ()_{, s x} - A_{44} () L_{45} = L_{54} = (B_{26} R^{- 1} - A_{45}) ()_{, x} + (B_{22} R^{- 1} - A_{44}) ()_{, s} L_{55} = - [A_{55} ()_{, x x} + 2 A_{45} ()_{, s x} + A_{44} ()_{, s s} - A_{22} R^{- 2} ()] ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

6.2 层合圆柱壳自由振动问题求解

如果只考虑圆柱壳的低频横向振动问题，则在方程 $(6.1.11)$ 右端仅保留了法向惯性力 $- \overline{ρ} w_{, t t}$ 一项。对于两端简支的特殊正交各向异性层合圆柱壳来说，其位移函数可假设为：

$u_{0} (x, θ, t) = m = 1 \sum \infty n = 0 \sum \infty U_{m n} cos \frac{m π x}{L} cos n θ e^{i ω t} v_{0} (x, θ, t) = m = 1 \sum \infty n = 0 \sum \infty V_{m n} sin \frac{m π x}{L} sin n θ e^{i ω t} α (x, θ, t) = m = 1 \sum \infty n = 0 \sum \infty A_{m n} cos \frac{m π x}{L} cos n θ e^{i ω t} β (x, θ, t) = m = 1 \sum \infty n = 0 \sum \infty B_{m n} sin \frac{m π x}{L} sin n θ e^{i ω t} w (x, θ, t) = m = 1 \sum \infty n = 0 \sum \infty W_{m n} sin \frac{m π x}{L} cos n θ e^{i ω t} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (6.2.1)$

在 $x = 0, L$ 处：

$w = 0, v_{0} = 0, β = 0 N_{x} = 0, M_{x} = 0} (6.2.2)$

将 $(6.2.1)$ 代入到 $(6.1.11)$ 后，即可得到无穷多组关于特定位移参数 $U_{m n}$ 、 $V_{m n}$ 、 $A_{m n}$ 、 $B_{m n}$ 和 $W_{m n}$ 的齐次代数方程组。通过分别取这些齐次代数方程组的系数矩阵行列式为零，即可求出相应的横向自振频率 $ω_{m n}$ 和振型。

当所研究的圆柱壳两端为嵌固支形式，则边界条件为，在 $x = 0, L$ 处：

$u_{0} = v_{0} = α = β = w = 0 (6.2.3)$

贝尔脱（Bert）等对这类圆柱壳的自由振动问题进行过精细的研究，他们给出的满足边界条件的解为：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u_{0} v_{0} α β w ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = n = 1 \sum N ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ U_{n} V_{n} V_{n} Γ_{n} W_{n} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ (1 - cos \frac{2 n π x}{L} sin n θ + sin \frac{n π x}{L} cos n θ) e^{i ω t} (6.2.4)$

需要注意得是，在计算材料具有较强的各向异性性质或计算比较短的壳体时以及在分析较高阶的自振频率时，应用经典壳体理论算出的结果都会导致严重的误差。

6.3 正交各向异性圆柱壳在局部法向载荷下弯曲问题的求解

如果研究一个两端简支的特殊正交各向异性圆柱壳在局部载荷 $p (x, θ)$ 作用下的弯曲问题。平衡方程可简化为：

$N_{x, x} + N_{x θ, s} = 0 N_{x θ, x} + N_{θ, x} + R^{- 1} Q_{θ z} = 0 Q_{x z, x} + Q_{θ z, s} - R^{- 1} N_{θ} = - p (x, θ) M_{x, x} + M_{x θ, s} - Q_{x z} = 0 M_{θ x, x} + M_{θ, s} - Q_{θ z} = 0 ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

几何方程仍然为 $(6.1.6)$ 、 $(6.1.7)$ 和 $(6.1.8)$ 式。

物理方程与 $(6.1.9)$ 相同。但 $Q_{x z}$ 和 $Q_{θ z}$ 可简化。
参考各向同性弹性壳中横向剪切变形对壳体弯曲的影响，近似取横向剪切应变为 $γ_{x z}$ 和 $γ_{θ z}$ 为：

$γ_{x z} = \frac{6}{5} \frac{Q _{x z}}{G _{x z} h} γ_{x θ} = \frac{6}{5} \frac{Q _{θ z}}{G _{θ z} h} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫$

将 $(6.1.8)$ 式代入后：

$Q_{x z} = \frac{5}{6} G_{x z} h (α + w_{, x}) Q_{θ z} h = \frac{5}{6} G_{θ z} h (β - R^{- 1} v_{0} + w_{, s}) ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫$

于是按照位移法求解三大方程，得位移形式表示得平衡方程：

$K_{x} [u_{o, x x} + v_{0 x} R^{- 1} (v_{0, x} + w_{, x}) + G_{x θ} h R^{- 1} (R^{- 1} u_{0, θ θ} + v_{0, x})] = 0 G_{x θ} h (R^{- 1} u_{0, x θ} + v_{0, x x}) + K_{θ} R^{- 1} [R^{- 1} (v_{0, θ θ} + w_{, θ}) + v_{x θ} u_{0, x θ}] + \frac{5}{6} R^{- 1} G_{θ z} h [β - R^{- 1} (v_{0} + w_{, θ})] = 0 \frac{5}{6} G_{x z} h (α_{, x} + w_{, x x}) + \frac{5}{6} R^{- 1} G_{θ z} h [β_{, θ} - R^{- 1} (v_{0, θ} + w_{, θ θ})] - K_{θ} R^{- 1} [R^{- 1} (v_{0, θ} + w) + v_{x θ} u_{0, x}] + p (x, θ) = 0 D_{x} (α_{, x x} + v_{, θ x} β_{, x θ} R^{- 1}) + \frac{G _{x θ} h ^{3}}{1 2} R^{- 1} (R^{- 1} α_{, θ θ} + β_{, x θ}) - \frac{5}{6} G_{x z} h (α + w_{, x}) = 0 \frac{G _{x θ} h ^{3}}{1 2} (R^{- 1} α_{, θ x} + β_{, x x}) + D_{θ} R^{- 1} (v_{x θ} α_{, x θ} + R^{- 1} β_{, θ θ}) - \frac{5}{6} G_{θ z} h [β - R^{- 1} (v_{0} - w_{, θ})] = 0 ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (6.3.1)$

式中：

$K_{i} = E_{i} h / (1 - v_{x θ} v_{θ x}) D_{i} = E_{i} h^{3} / 12 (1 - v_{x θ} v_{θ x})}$

壳体承受局部载荷作用的情况如图所示，
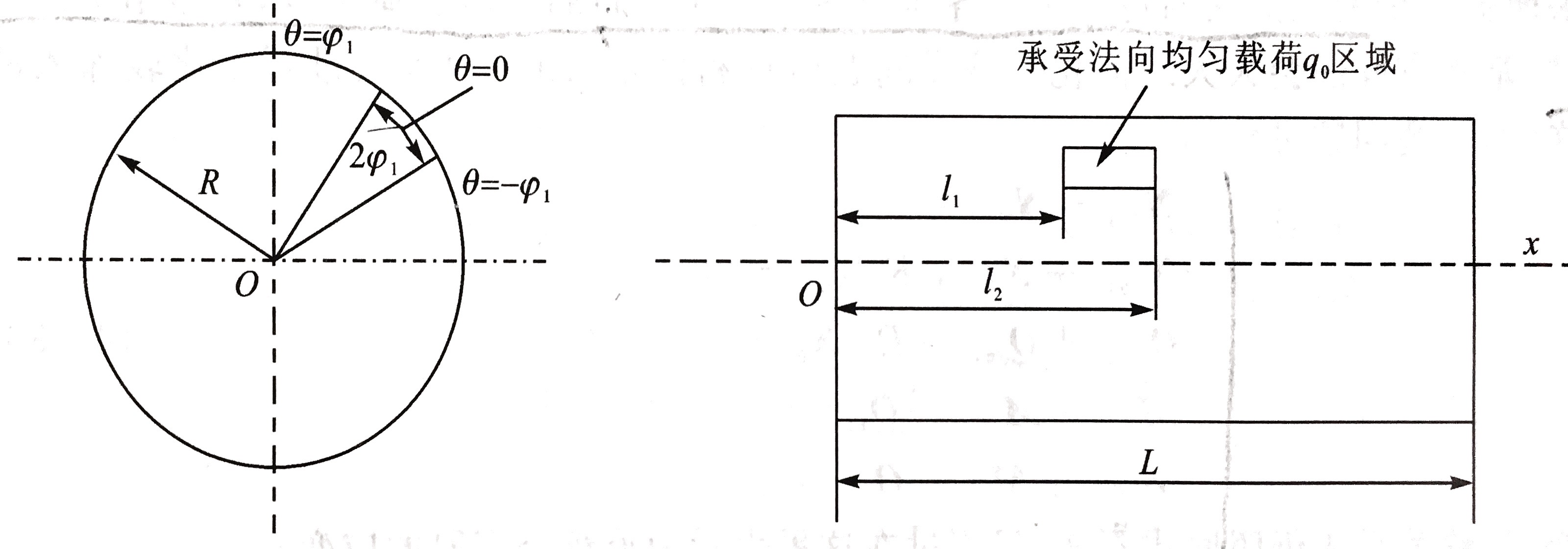
正方形基本单元
为了避免与边界弯曲效应的相互干扰，载荷作用面积应该离开圆柱壳两端有一定的距离，而边缘弯曲效应在轴向的长度取为 $4 (E_{x} / E_{θ})^{1 / 2} R h$ ，所以一般使载荷作用面积距离圆柱壳两端边界大于这一特征长度即可。

现在假设载荷作用区域为 $l_{1} \leq x_{1} \leq l_{2}$ 和 $- ϕ_{1} \leq θ \leq + ϕ_{1}$ 。为了满足基本方程式 $(6.3.1)$ 和两端简支的边界条件，将该问题的解取成为标准的双重三角级数形式：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u_{0} v_{0} w α β p ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = n = 0 \sum \infty m = 1 \sum \infty ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ U_{m n} cos n θ cos \frac{m π x}{L} V_{m n} sin n θ sin \frac{m π x}{L} W_{m n} cos n θ sin \frac{m π x}{L} A_{m n} cos n θ cos \frac{m π x}{L} B_{m n} sin n θ sin \frac{m π x}{L} P_{m n} cos n θ sin \frac{m π x}{L} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ e^{i w t} (6.3.2)$

式中，如果载荷分布 $p (x, θ) = p_{0}$ 为一常数，则有：

$P_{m n} = {\frac{2 p _{0} ϕ _{1}}{m π ^{2}} [cos (\frac{m π L _{1}}{L}) - cos (\frac{m π l _{2}}{L})] (n = 0, m \neq = 0) \frac{4 p _{0}}{m n π ^{2}} [cos (\frac{m π L _{1}}{L}) - cos (\frac{m π l _{2}}{L})] sin n ϕ_{1} (n \neq = 0, m \neq = 0)$

将 $(6.3.2)$ 代入 $(6.3.1)$ 中，即可得到如下的一组代数方程式：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ F_{11} F_{21} F_{31} F_{41} F_{51} F_{12} F_{22} F_{32} F_{42} F_{52} F_{13} F_{23} F_{33} F_{43} F_{53} F_{14} F_{24} F_{34} F_{44} F_{54} F_{15} F_{25} F_{35} F_{45} F_{55} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ U_{m n} V_{m n} W_{m n} B_{m n} A_{m n} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ F F_{1} F F_{2} F F_{3} F F_{4} F F_{5} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ (6.3.3)$

其中各系数 $F_{i j} (i, j = 1, 2, \dots, 5)$ 为：

$F_{11} = K_{θ} R^{- 1} v_{x θ} (m π L^{- 1}) F_{12} = - n R^{- 2} (\frac{5}{6} G_{θ z} h + K) F_{13} = - \frac{5}{6} G_{θ z} h (m π L^{- 1})^{2} - \frac{5}{6} G_{θ z} h (n R^{- 1})^{2} - K_{θ} R^{- 2} F_{14} = \frac{5}{6} G_{θ z} h n R^{- 1} F_{15} = - \frac{5}{6} G_{x z} h m π L^{- 1} F_{21} = - K_{x} (m π L^{- 1})^{2} G_{x θ} h (n R^{- 1})^{2} F_{22} = (n R^{- 1}) (m π L^{- 1}) (K_{x} v_{θ x} + G_{x θ} h) F_{23} = K_{x} R^{- 1} v_{x θ} (m π L^{- 1}) F_{24} = F_{25} = 0 F_{31} = (n R^{- 1}) (m π L^{- 1}) (K_{θ} v_{θ x} + G_{x θ} h) F_{32} = - G_{x θ} h (m π L^{- 1})^{2} - K_{θ} (n R^{- 1})^{2} - \frac{5}{6} G_{θ z} h R^{- 2} F_{33} = - n R^{- 2} (\frac{5}{6} G_{θ z} h + K_{θ}) F_{34} = \frac{5}{6} G_{θ z} h R^{- 1} F_{35} = F_{41} = F_{42} = 0 F_{43} = - \frac{5}{6} G_{x z} h m π L^{- 1} F_{44} = (n R^{- 1}) (m π L^{- 1}) (D_{x} v_{x} + \frac{1}{1 2} G_{x θ} h^{3}) F_{45} = - (m π L^{- 1})^{2} D_{x} - \frac{1}{1 2} (n R^{- 1})^{2} G_{x θ} h^{3} - \frac{5}{6} G_{x z} h F_{51} = 0 F_{52} = \frac{5}{6} G_{θ z} h R^{- 1} F_{53} = \frac{5}{6} n R^{- 1} G_{θ z} h F_{54} = - \frac{1}{1 2} (m π L^{- 1})^{2} G_{x θ} h^{3} - (n R^{- 1})^{2} D_{θ} - \frac{5}{6} G_{θ z} h F_{55} = (n R^{- 1}) (m π L^{- 1}) (D_{θ} v_{x} + \frac{1}{1 2} G_{x θ} h^{3}) ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

$F F_{i}$ 是和载荷 $p_{0}$ 及作用面积有关的系数：

$F F_{1} = {- \frac{4 P _{0} ϕ _{1}}{m π ^{2}} sin m π (\frac{l _{1} + l _{2}}{2 L}) sin m π (\frac{l _{2} - l _{1}}{2 L}) (n = 0) - \frac{8 P _{0}}{m n π ^{2}} sin (n ϕ_{1}) sin m π (\frac{l _{1} + l _{2}}{2 L}) sin m π (\frac{l _{2} - l _{1}}{2 L}) (n \neq = 0) F F_{2} = F F_{3} = F F_{4} = F F_{5} = 0$

解方程 $(6.3.3)$ ，可以得出位移函数，代入物理方程求得内力。壳中的应力按如下公式可求出：

$σ_{x} (x, θ, z) = \frac{N _{x} ( x , θ )}{h} + \frac{1 2 M _{x} ( x , θ ) z}{h ^{3}} σ_{θ} (x, θ, z) = \frac{N _{θ} ( x , θ )}{h} + \frac{1 2 M _{θ} ( x , θ ) z}{h ^{3}} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫ (6.3.4)$

从各种计算结果，得到一下结论：

一般来说，当 $E_{x} > E_{θ}$ 时 $M_{x} > M_{θ}$ 。当 $E_{i} / E_{j}$ 增加时， $N_{i}$ 和 $M_{i}$ 也随着增大，同时 $N_{j}$ 和 $M_{j}$ 随着减小（ $i, j = x, θ$ ）。
载荷的分布越集中，最大弯曲应力值就越高。一般 $M_{x}$ 和 $M_{θ}$ 的最大值发生在载荷分布区域接近正方形的情况。
当壳体厚度（ $h / R$ ）增大时， $M_{x}$ 也随着增大。
当载荷的周向分布角 $ϕ_{1}$ 增大时， $M_{x}$ 也随着增大。当载荷分布区域的轴向长度大于周向长度即 $(l_{1} - l_{2}) > 2 ϕ_{1}$ 时， $N_{x}$ 受载荷分布段几何尺寸变化的影响不敏感。
虽然对各向同性薄壳在局部载荷作用下的应力分析，横向剪切变形的影响是可忽略的；但是，对于复合材料层合薄壳在局部载荷作用下进行应力分析时，横向剪切变形的效应相当显著，是不应该轻易忽略的。

7 复合材料层合结构有限元分析

7.1 形函数和位移模式

这里采用和各向同性板中面一样的八结点单元，板的每个节点有5个参数，分别是中面沿 $x$ 、 $y$ 、 $z$ 轴的位移和中面法线绕 $x$ 、 $y$ 轴的转角，即 $u_{0}$ 、 $v_{0}$ 、 $w_{0}$ 、 $α$ 及 $β$ 。

取典型的板单元，在中面上以所研究点为原点建立局部坐标系 $O - ξ η ζ$ ，如图所示：
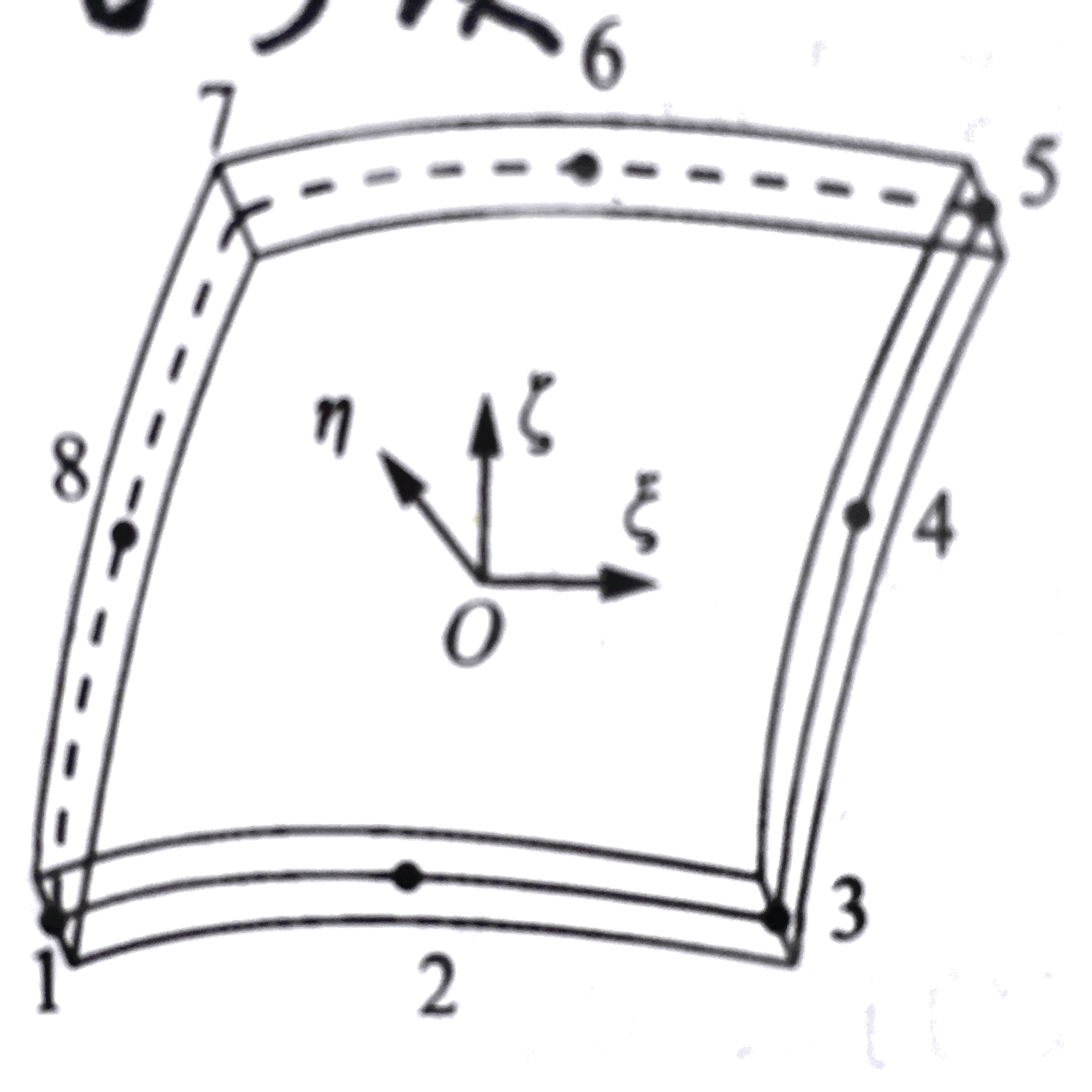
正方形基本单元
将 $z$ 轴垂直于中面，则曲线四边形的实际单元如图所示：

根据泰勒展开，在中面上，设单元内的一点在绝对坐标系 $O - x y z$ 下的坐标 $x^{(0)}$ 、 $y^{(0)}$ 和 $z^{(0)}$ （在中面上 $z$ 是 $x$ 和 $y$ 的函数），可在局部坐标系 $O - ξ η ζ$ 中近似写为（即坐标变换）：

$x^{(0)} = a_{1} + a_{2} ξ + a_{3} η + a_{4} ξ^{2} + a_{5} ξ η + a_{6} η^{2} + a_{7} ξ^{2} η + a_{8} ξ η^{2} y^{(0)} = b_{1} + b_{2} ξ + b_{3} η + b_{4} ξ^{2} + b_{5} ξ η + b_{6} η^{2} + b_{7} ξ^{2} η + b_{8} ξ η^{2} z^{(0)} = c_{1} + c_{2} ξ + c_{3} η + c_{4} ξ^{2} + c_{5} ξ η + c_{6} η^{2} + c_{7} ξ^{2} η + c_{8} ξ η^{2} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫$

写成矩阵形式：

$⎣ ⎢ ⎡ x^{(0)} y^{(0)} z^{(0)} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ a_{1} b_{1} c_{1} \dots \dots \dots a_{8} b_{8} c_{8} ⎦ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 ξ η ξ^{2} ξ η η^{2} ξ^{2} η ξ η^{2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ (7.1.1)$

由于有8个结点的局部坐标 $(ξ_{i}, η_{i}, ζ)$ 和绝对坐标 $(x_{i}^{(0)}, y_{i}^{(0)}, z_{i}^{(0)})$ $(i = 1, 2, \dots, 8)$ ，于是可写出矩阵方程：

$⎣ ⎢ ⎢ ⎡ x_{1}^{(0)} y_{1}^{(0)} z_{1}^{(0)} \dots \dots \dots x_{8}^{(0)} y_{8}^{(0)} z_{8}^{(0)} ⎦ ⎥ ⎥ ⎤_{(3 \times 8)} = ⎣ ⎢ ⎡ a_{1} b_{1} c_{1} \dots \dots \dots a_{8} b_{8} c_{8} ⎦ ⎥ ⎤_{(3 \times 8)} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 ξ_{1} η_{1} ξ_{1}^{2} ξ_{1} η_{1} η_{1}^{2} ξ_{1}^{2} η_{1} ξ_{1} η_{1}^{2} \dots \dots \dots \dots \dots \dots \dots \dots 1 ξ_{8} η_{8} ξ_{8}^{2} ξ_{8} η_{8} η_{8}^{2} ξ_{8}^{2} η_{8} ξ_{8} η_{8}^{2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤_{(8 \times 8)}$

于是：

$⎣ ⎢ ⎡ a_{1} b_{1} c_{1} \dots \dots \dots a_{8} b_{8} c_{8} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x_{1}^{(0)} y_{1}^{(0)} z_{1}^{(0)} \dots \dots \dots x_{8}^{(0)} y_{8}^{(0)} z_{8}^{(0)} ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 ξ_{1} η_{1} ξ_{1}^{2} ξ_{1} η_{1} η_{1}^{2} ξ_{1}^{2} η_{1} ξ_{1} η_{1}^{2} \dots \dots \dots \dots \dots \dots \dots \dots 1 ξ_{8} η_{8} ξ_{8}^{2} ξ_{8} η_{8} η_{8}^{2} ξ_{8}^{2} η_{8} ξ_{8} η_{8}^{2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤^{- 1}$

将上式回代入 $(7.1.1)$ ：

$⎣ ⎢ ⎡ x^{(0)} y^{(0)} z^{(0)} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x_{1}^{(0)} y_{1}^{(0)} z_{1}^{(0)} \dots \dots \dots x_{8}^{(0)} y_{8}^{(0)} z_{8}^{(0)} ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 ξ_{1} η_{1} ξ_{1}^{2} ξ_{1} η_{1} η_{1}^{2} ξ_{1}^{2} η_{1} ξ_{1} η_{1}^{2} \dots \dots \dots \dots \dots \dots \dots \dots 1 ξ_{8} η_{8} ξ_{8}^{2} ξ_{8} η_{8} η_{8}^{2} ξ_{8}^{2} η_{8} ξ_{8} η_{8}^{2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤^{- 1} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 ξ η ξ^{2} ξ η η^{2} ξ^{2} η ξ η^{2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

其中各结点的相对坐标的值如图所示：
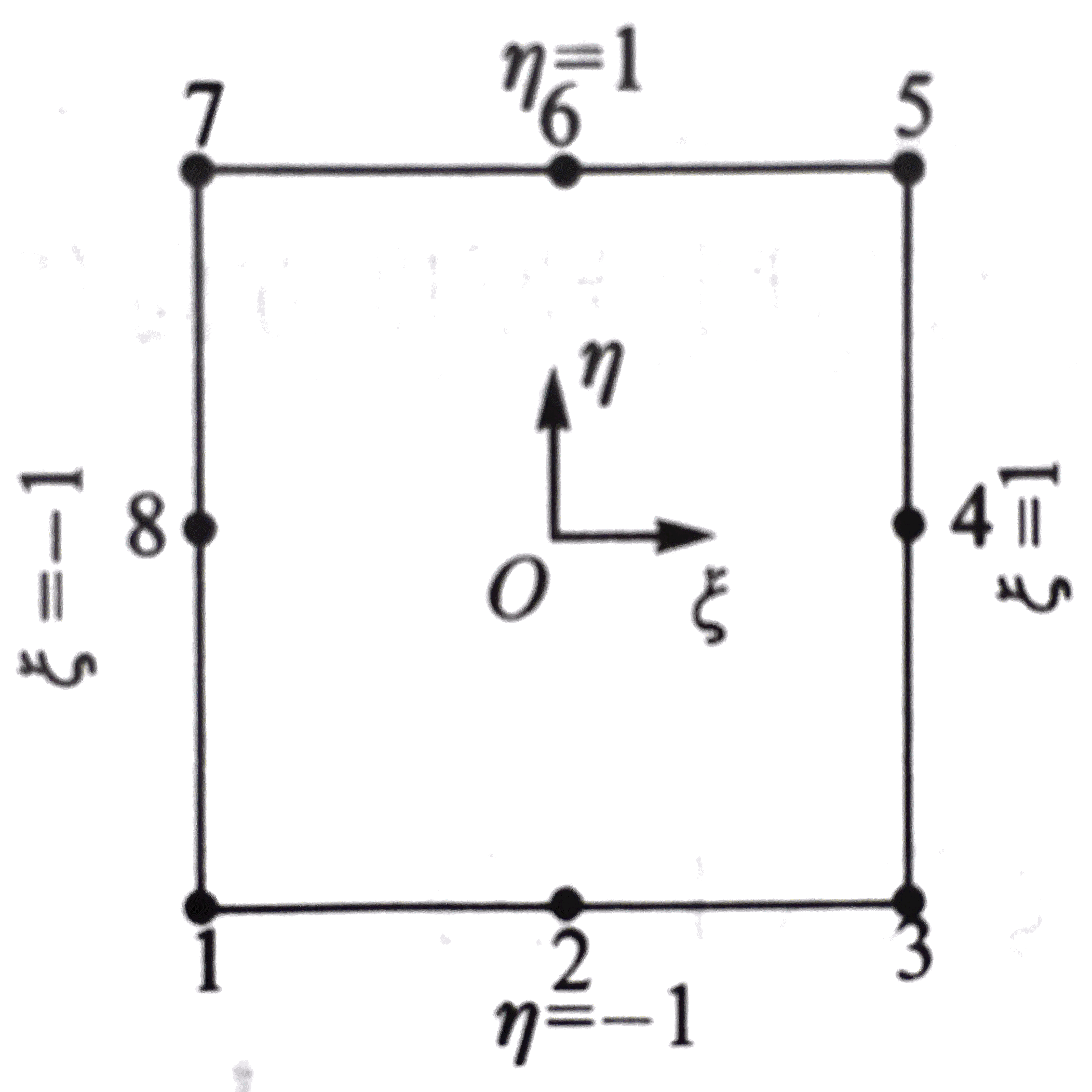
正方形基本单元
得：

$⎣ ⎢ ⎡ x^{(0)} y^{(0)} z^{(0)} ⎦ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ x_{1}^{(0)} y_{1}^{(0)} z_{1}^{(0)} \dots \dots \dots x_{8}^{(0)} y_{8}^{(0)} z_{8}^{(0)} ⎦ ⎥ ⎥ ⎤ \frac{1}{4} ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ - 1 2 - 1 2 - 1 2 - 1 2 0002000 - 2 0 - 2 000200 1 - 2 101 - 2 10 10 - 1 010 - 1 0 101 - 2 101 - 2 - 1 2 - 1 01 - 2 10 - 1 01 - 2 10 - 1 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1 ξ η ξ^{2} ξ η η^{2} ξ^{2} η ξ η^{2} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

可改写成：

$x^{(0)} = i = 1 \sum 8 N_{i} x_{i}^{(0)} y^{(0)} = i = 1 \sum 8 N_{i} y_{i}^{(0)} z^{(0)} = i = 1 \sum 8 N_{i} z_{i}^{(0)} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (i = 1, 2, \dots, 8) (7.1.2)$

其中， $N_{i}$ 为形函数：

$N_{1} = \frac{1}{4} (1 - ξ) (1 - η) (- ξ - η - 1) N_{2} = \frac{1}{2} (1 - ξ^{2}) (1 - η) N_{3} = \frac{1}{4} (1 + ξ) (1 - η) (ξ - η - 1) N_{4} = \frac{1}{2} (1 + ξ) (1 - η^{2}) N_{5} = \frac{1}{4} (1 + ξ) (1 + η) (ξ + η - 1) N_{6} = \frac{1}{2} (1 - ξ^{2}) (1 + η) N_{7} = \frac{1}{4} (1 - ξ) (1 + η) (- ξ + η - 1) N_{8} = \frac{1}{2} (1 - ξ) (1 - η^{2}) ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (7.1.3)$

根据 $(7.1.2)$ 可以写出中面的位移模式：

$u_{0} = i = 1 \sum 8 N_{i} (u_{0})_{i} v_{0} = i = 1 \sum 8 N_{i} (v_{0})_{i} w_{0} = i = 1 \sum 8 N_{i} (w_{0})_{i} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (i = 1, 2, \dots, 8)$

将 $z$ 轴放置于垂直于中面处且原点位于中面内。 $t$ 为某点处的板的总厚度，令 $ζ = 2 z / t$ （将 $ζ$ 令为表征厚度方向上位置的无量纲参数），则：

$z = \frac{ζ}{2} t$

由层合板理论:

$u = u_{0} + z α v = v_{0} + z β w = w_{0} ⎭ ⎪ ⎪ ⎬ ⎪ ⎪ ⎫$

于是：

$u = i = 1 \sum 8 N_{i} (u_{0})_{i} + \frac{ζ}{2} t α v = i = 1 \sum 8 N_{i} (v_{0})_{i} + \frac{ζ}{2} t β w = i = 1 \sum 8 N_{i} (w_{0})_{i} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

由于 $t$ 、 $α$ 和 $β$ 都只为 $x$ 和 $y$ 的函数，故可以采用形函数表示 $t α$ 和 $t β$ 。同时，去掉下标中的 $0$ 。于是上式可写为：

$u = i = 1 \sum 8 N_{i} u_{i} + \frac{ζ}{2} i = 1 \sum 8 N_{i} t_{i} α_{i} v = i = 1 \sum 8 N_{i} v_{i} + \frac{ζ}{2} i = 1 \sum 8 N_{i} t_{i} β_{i} w = i = 1 \sum 8 N_{i} w_{i} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫ (7.1.4)$

这就是单元的位移模式。

7.2 单元的应变应力列阵

这里仅考虑平板，即在直线直角坐标系下几何方程为：

$ϵ_{x} = \frac{\partial u}{\partial x}, ϵ_{y} = \frac{\partial v}{\partial y}, ϵ_{z} = \frac{\partial w}{\partial z} γ_{y z} = \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}, γ_{z x} = \frac{\partial w}{\partial x} + \frac{\partial u}{\partial z}, γ_{x y} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫$

于是得应变列阵：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} γ_{x z} γ_{y z} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ N_{, x} O N_{, y} O O O N_{, y} N_{, x} O O O O O N_{, x} N_{, y} \frac{ζ}{2} N_{, x} t O \frac{ζ}{2} N_{, y} t \frac{ζ _{, z}}{2} N t O O \frac{ζ}{2} N_{, y} t \frac{ζ}{2} N_{, x} t O \frac{ζ _{, z}}{2} N t ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ u v w α β ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

其中，下标中的逗号“ $,$ ”表示对逗号后面的变量求偏导。子矩阵为：

$N = [N_{1} N_{2} \dots N_{8}] t = ⎣ ⎢ ⎢ ⎢ ⎡ t_{1} t_{2} ⋱ t_{8} ⎦ ⎥ ⎥ ⎥ ⎤ u = [u_{1} u_{2} \dots u_{8}]^{T} v = [v_{1} v_{2} \dots v_{8}]^{T} w = [w_{1} w_{2} \dots w_{8}]^{T} α = [α_{1} α_{2} \dots α_{8}]^{T} β = [β_{1} β_{2} \dots β_{8}]^{T} ⎭ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎫$

于是可简写为：

$ϵ = B δ^{e} (7.2.5)$

复合材料的物理方程为：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} σ_{z} τ_{x y} τ_{x z} τ_{y z} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ \overline{C}_{11} \overline{C}_{21} \overline{C}_{31} \overline{C}_{41} 00 \overline{C}_{12} \overline{C}_{22} \overline{C}_{32} \overline{C}_{42} 00 \overline{C}_{13} \overline{C}_{23} \overline{C}_{33} \overline{C}_{43} 00 \overline{C}_{14} \overline{C}_{24} \overline{C}_{34} \overline{C}_{44} 00 0000 \overline{C}_{55} \overline{C}_{65} 0000 \overline{C}_{56} \overline{C}_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} ϵ_{z} γ_{x y} γ_{x z} γ_{y z} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ (7.2.6)$

其中： $\overline{C}$ 为偏轴时的三维模量矩阵。注意：在查阅 $\overline{C}$ 时，由于 $ϵ$ 的元素排列顺序不同，可能需要将 $\overline{C}$ 元素的位置调整。

由于已假设 $σ_{z} = 0$ ，即：

$σ_{z} = \overline{C}_{31} ϵ_{x} + \overline{C}_{32} ϵ_{y} + \overline{C}_{33} ϵ_{z} + \overline{C}_{31} γ_{x y} = 0$

得：

$ϵ_{z} = - \frac{1}{C _{33}} (\overline{C}_{31} ϵ_{x} + \overline{C}_{32} ϵ_{y} + \overline{C}_{34} γ_{x y})$

将上式回代入 $(7.2.6)$ 得：

$⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ σ_{x} σ_{y} τ_{x y} τ_{x z} τ_{y z} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ D_{11} D_{21} D_{31} 00 D_{12} D_{22} D_{32} 00 D_{13} D_{23} D_{33} 00 000 D_{44} D_{64} 000 D_{46} D_{66} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ϵ_{x} ϵ_{y} γ_{x y} γ_{x z} γ_{y z} ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

式中：

$D_{i j} D_{(i - 1) (j - 1)}} = \overline{C}_{i j} - \frac{C _{i 3} C _{j 3}}{C _{33}} (i, j = 1, 2) (i, j = 4, 5, 6)$

或简写成：

$σ = D ϵ$

代入 $(7.2.5)$ 中得：

$σ = D B δ^{e} (7.2.7)$

7.3 单元的劲度矩阵和平衡方程

单元的内力势能，即应变能为：

$U = \frac{1}{2} \int_{V} ϵ^{T} σ d V$

外力势能：

$V = - (δ^{e})^{T} F_{L}^{e}$

其中， $F_{L}^{e}$ 为结点上的结点载荷，为将单元所受外力按照虚功等效移置在结点上的力：

$F_{L}^{e} = \sum N^{T} f_{p} + \int_{S} N^{T} \overline{f} d S + \int_{V} N^{T} f d V (7.3.1)$

$f_{p}$ 、 $\overline{f}$ 和 $f$ 分别为集中力、面力和体力。

于是总势能为：

$E_{p} = U + V = \frac{1}{2} \int_{V} ϵ^{T} σ d V - (δ^{e})^{T} F_{L}^{e}$

将 $(7.2.5)$ 和 $(7.2.7)$ 代入上式：

$E_{p} = \frac{1}{2} (δ^{e})^{T} \int_{V} B^{T} D B d V δ^{e} - (δ^{e})^{T} F_{L}^{e}$

由最小势能原理：

$\frac{\partial E _{p}}{\partial δ _{i}^{e}} = O$

矩阵求导运算有：

$\frac{\partial}{\partial a} (a^{T} b a) = 2 b a \frac{\partial}{\partial a} (a^{T} c) = c$

于是得：

$\int_{V} B^{T} D B d V δ^{e} - F_{L}^{e} = O$

即：

$F_{L}^{e} = \int_{V} B^{T} D B d V δ^{e}$

令单元的劲度矩阵为：

$K = \int_{V} B^{T} D B d V (7.3.2)$

则可得单元的平衡方程：

$F_{L}^{e} = K δ^{e} (7.3.3)$

对于劲度矩阵的运算，可以先利用雅可比矩阵 $J$ 由全局坐标变换为局部坐标：

$K = \int_{V} B^{T} D B d V = \int_{- 1}^{1} \int_{- 1}^{1} \int_{- 1}^{1} B^{T} D B ∣ J ∣ d ξ d η d ζ J = ⎣ ⎢ ⎢ ⎡ \frac{\partial x}{\partial ξ} \frac{\partial x}{\partial η} \frac{\partial x}{\partial ζ} \frac{\partial y}{\partial ξ} \frac{\partial y}{\partial η} \frac{\partial y}{\partial ζ} \frac{\partial z}{\partial ξ} \frac{\partial z}{\partial η} \frac{\partial z}{\partial ζ} ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎡ \sum \frac{\partial N _{i}}{\partial ξ} x_{i} \sum \frac{\partial N _{i}}{\partial η} x_{i} 0 \sum \frac{\partial N _{i}}{\partial ξ} y_{i} \sum \frac{\partial N _{i}}{\partial η} y_{i} 0 \frac{1}{2} \sum \frac{\partial N _{i}}{\partial ξ} t_{i} ζ \frac{1}{2} \sum \frac{\partial N _{i}}{\partial η} t_{i} ζ \frac{1}{2} \sum N_{i} t_{i} ⎦ ⎥ ⎤$

然后再利用高斯积分法（详情点击这里）：

$\int_{- 1}^{1} \int_{- 1}^{1} \int_{- 1}^{1} f (ξ, η, ζ) d ξ d η d ζ = i = 1 \sum n_{1} j = 1 \sum n_{2} m = 1 \sum n_{3} H_{i} H_{j} H_{m} f (ξ, η, ζ)$

$n_{1}$ 、 $n_{2}$ 和 $n_{3}$ 为积分点的数目； $H_{i}$ 、 $H_{j}$ 和 $H_{m}$ 为加权系数； $ξ$ ， $η$ 和 $ζ$ 为局部坐标系中积分点的坐标值。

即可算出劲度矩阵。

7.4 整体平衡方程

将所有壳单元建立的平衡方程写在一起：

$F_{L}^{e}_{(5 N) \times 1} = K_{(5 N) \times (5 N)} δ^{e}_{(5 N) \times 1}$

式中， $N$ 为节点总数； $δ^{e}$ 为所有的结点位移列向量； $F_{L}^{e}$ 为所有的节点载荷列向量：

$δ_{i}^{e} = [u_{i} v_{i} w_{i} α_{i} β_{i}]^{T} (F_{L}^{e})_{i} = [(F_{L}^{e})_{i x} (F_{L}^{e})_{i y} (F_{L}^{e})_{i z} (M_{L}^{e})_{i x} (M_{L}^{e})_{i y}]^{T} (i = 1, 2, \dots, N)$

根据边界条件和载荷，利用 $(7.3.1)$ 即可得到 $F_{L}^{e}$ 。代入上面方程即可求得各节点位移 $δ^{e}$ ，进而求得应力应变。

8 总结

复合材料结构力学是以各向同性的弹性力学为基础，引入各向异性的材料性质，对其推广。研究了复合梁、层合板、层合壳等结构。
复合梁有层合梁和板梁两种。层合梁具有耦合弯扭拉耦合效应。板梁弯曲时，其拉应力不沿集合中面对称分布。
夹层板的设计主要是考虑了平板受弯时的应力，让远离中面材料受弯，让中面材料受剪。
分析层合板在弯曲和屈曲时会有拉压-弯曲耦合，书中选用了对称层合板或者没有考虑。在分析层合板振动时，书中没有考虑转动惯量的影响。
各向异性层合圆柱壳是一种壳体，它的几何方程在正交曲线坐标系下的形式与普通直线正交坐标的形式有所不同。
克希荷夫（Kirchhoff）的直法线假设是层合板基本假设之一。在分析层合壳时，该假设部分成立。
书中，复合材料层合结构的有限元单元采用四边形八节点单元。

本文章使用limfx的vsocde插件快速发布