Linear algebra

回到主页

这一次复习，我希望可以弄清楚线代的几何意义，线代究竟是怎么出来的，它究竟该怎么用，有哪些真正的物理上的含义，而不是曾经晦涩难懂的莫名其妙的定义，一些忘记了就不会再记得第二遍的东西

本次学习使用http://immersivemath.com/ila/ch00_preface/preface.html作为教材来源

https://zhuanlan.zhihu.com/p/199665495 深感认同

vector

行矢量列矢量转置The transpose of a vector

其实某种函数也可以看成矢量，举例如下：

image-20200905091923048

基底Basis

柯西公式（等我有时间了专门来分析下柯西公式可以在哪些领域使用）image-20200905091923048

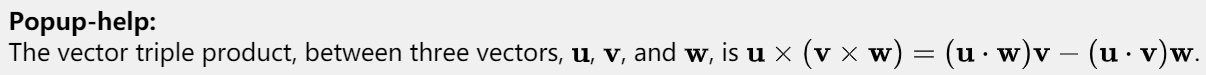
image-20200905094238546

高斯消除法 Gaussian Elimination

image-20200905094600156

矩阵The Matrix

Matrices are a very powerful tool to manipulate data with.看它这里指的矩阵的意思是用来manipulate data，这个说法就很有意思，它是一种变换，是一种映射方式

把高斯消除法写成矩阵形式such as this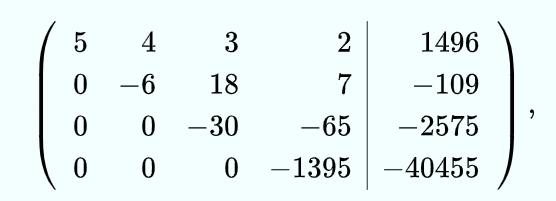image-20200905094600156

rotation

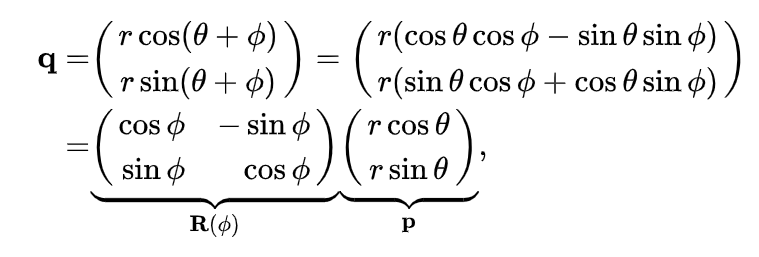
image-20200905102504372

scaling 缩放

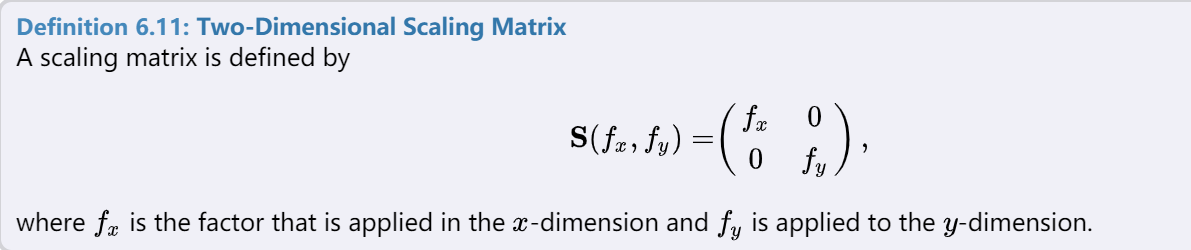
image-20200905102504372

求矩阵的逆矩阵的方法

AX=IB=》IX=A^-1B

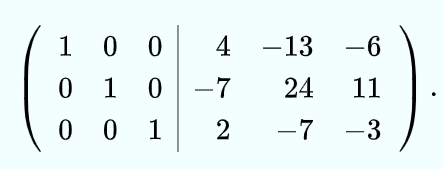
image-20200905102658115

和高斯规则相同

正交矩阵Orthogonal Matrices

Definition 6.18: Orthogonal Matrix An orthogonal matrix B is a square matrix where the column vectors constitute an orthonormal basis.正交矩阵B是一个正方形矩阵，其中列向量构成了正交标准。

image-20200905102850592

an orthonormal basis：它的列向量都是单位向量，且两两正交

旋转矩阵

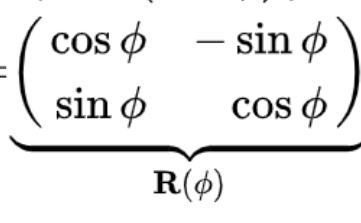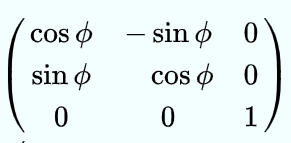
image-20200905102850592或image-20200905103328578

是正交矩阵

正交矩阵对矢量进行处理不会改变它的模长

正交矩阵乘正交矩阵后还是正交矩阵

正交矩阵处理后的矢量之间的性质不变

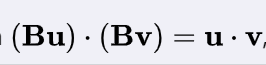
image-20200905103344123

正交矩阵相当于坐标变换（找基底什么的）认真看下面这个例子就能理解了

image-20200905112712949

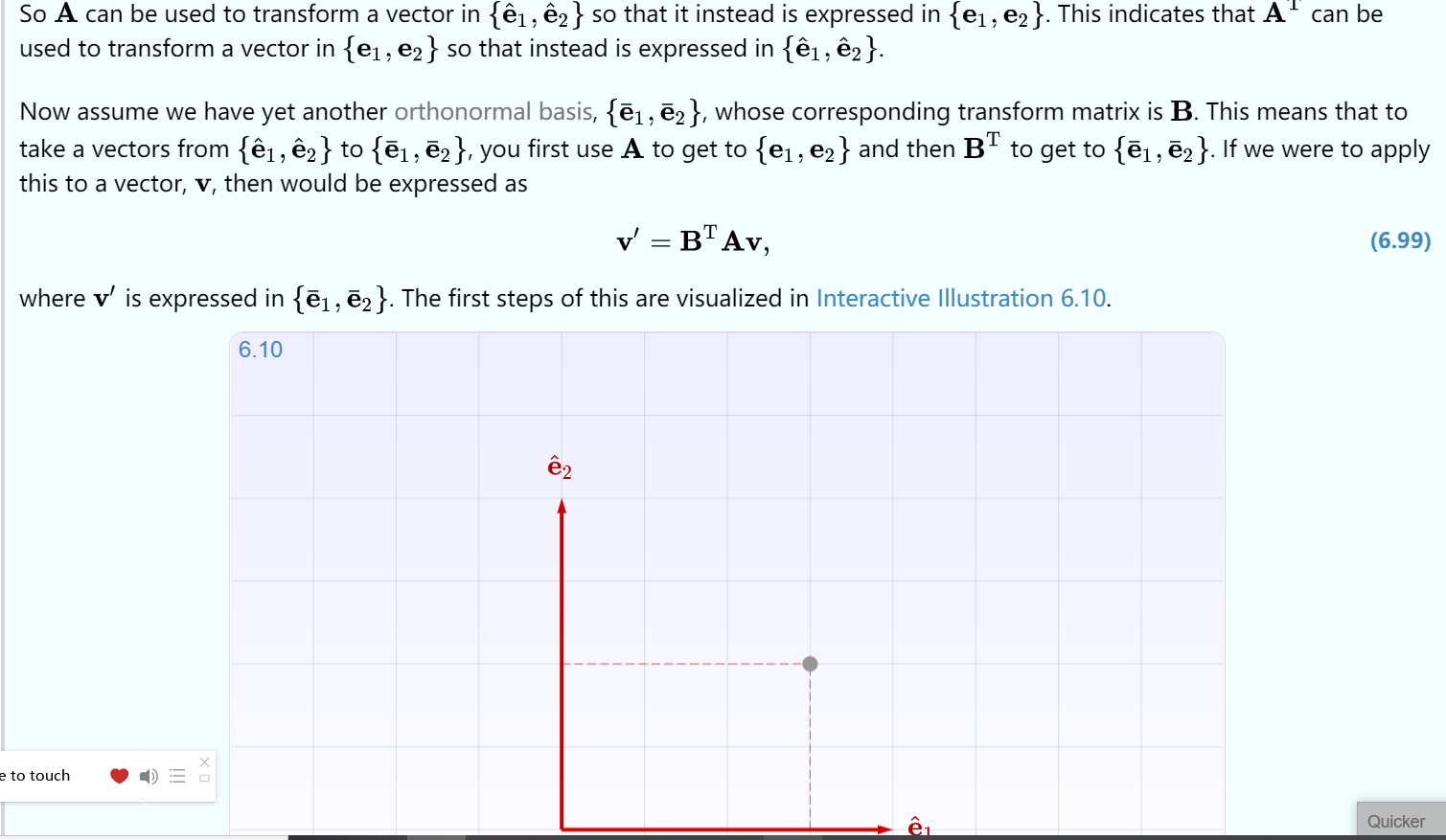
image-20200905112752358

行列式Determinants

image-20200905112752358

image-20200905112832618

伴随矩阵

image-20200905114355741

image-20200905114546688

求方程的方法2image-20200905114546688

Cramer's rule.

秩 Rank

线性空间 linear vector space

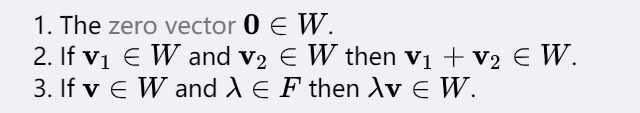
image-20200905114753405

image-20200905114546688

image-20200905114753405

image-20200905114949386

nullity，是Null Space 的维度，是方程未知量个数减A的秩

image-20200905115925133

秩

image-20200905115607950

image-20200905115629504

image-20200905115746618

image-20200905115912810

linear mappings

In linear algebra, the term mapping is traditionally used instead of function, but the meaning is the same,

image-20200906200822955

image-20200907070115691

image-20200907070445755

image-20200907070519997

这个证明有点意思，贴上来

image-20200907070617378

image-20200907070743222

image-20200907071051792

这个还是挺有意思的，F里面每一个列向量都是对ei进行F变换得来的

image-20200907071309389

好，开始矩阵相乘的运用了

image-20200907072159751

一一对应

image-20200907072319419

全体映射

image-20200907072351835

一一对应+全体映射

A-》B B-》A 好了应该要开始可逆了

image-20200907072447113

image-20200907090315564

越来越有意思咯，这种mapping

特征值和特征向量 Eigenvalues and Eigenvectors

image-20200907114422164

image-20200907114659144

特征值方程

image-20200907115013957

对角化

image-20200907115031188

image-20200907115103323

image-20200907115203988

对那个多项式的解释

image-20200907115305691

image-20200907115354329

image-20200907115405213

这个网站对这些东西的定义没有学校给它定义定义的好，还是看学校的那个对角化知识把，反正现在也在教嘛，可以教到了再细看

结尾的话

其实把线代看下来，会真的对国内的线代教学产生恶感，流畅的逻辑就应该是从向量到线性空间，从线性空间的变换到矩阵，从矩阵到行列式再到mapping，再从mapping到特征值特征向量这些东西

现在感觉最深的就是线代的使用，尤其是增广矩阵的运算和可逆的运算，要常学

其实本来以为9-5号就能学完的，居然硬生生学了三天，还是记忆不行呀

本文章使用limfx的vsocde插件快速发布