复合材料结构力学涉猎（上）

• 1 绪论
• 2 各向异性材料弹性力学基础
  • 2.1 几何方程与变形协调条件
  • 2.2 平衡方程
  • 2.3 物理方程
  • 2.4 弹性力学的一般解法
• 3 复合材料梁
  • 3.1 复合材料层合梁分析
    • 3.1.1 层合梁的抗弯刚度和应力
    • 3.1.2 层合梁的中性面位置
    • 3.1.3 层合梁的剪应力
  • 3.2 复合材料板梁分析
• 4 夹层结构分析
  • 4.1 夹层板分析基础
  • 4.2 蜂窝夹层结构的工程计算
    • 4.2.1 蜂窝夹层结构的密度计算
    • 4.2.2 蜂窝夹层结构的等效弹性模量计算
      • 4.2.2.1 面内拉伸弹性模量
      • 4.2.2.2 蜂窝夹层结构的剪切模量
      • 4.2.2.3 蜂窝芯料的剪切模量
      • 4.2.2.4 蜂窝夹层结构的平拉（或平拉）模量

1 绪论

复合材料结构分析是对由复合材料构成的具体构件，以基本力学性能为基础，考虑构件所处的边界条件，计算其应力与应变的分布规律。这些内容被称为复合材料结构力学。这些基本件包括杆、梁、板、壳等结构元件。

涉及的知识：材料力学、弹性力学、单层复合材料力学、层合板复合材料力学、有限元素法基础、结构动力学基础、高等数学、线性代数

2 各向异性材料弹性力学基础

对于复合材料的构件进行结构分析时，均假定其在载荷作用下变形很小，且在弹性变形范围内，因此采用弹性力学的基本方法。

2.1 几何方程与变形协调条件

设$u$、$v$、$w$为直角坐标系下的位移分量，${ϵ}_x$、${ϵ}_y$、${ϵ}_z$、${\gamma }_{yz}$、${\gamma }_{zx}$、${\gamma }_{xy}$为应变分量，则在小变形条件下，它们的关系，即几何方程为：

$$\begin{array}{rl}& {ϵ}_x=\frac{\partial u}{\partial x},{ϵ}_y=\frac{\partial v}{\partial y},{ϵ}_z=\frac{\partial w}{\partial z}\\ & {\gamma }_{yz}=\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y},{\gamma }_{zx}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z},{\gamma }_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\end{array}\}$$

将上式中消去位移$u$、$v$、$w$后可得：

$$\begin{array}{rl}& \frac{{\partial }^2{\gamma }_{xy}}{\partial x\partial y}=\frac{{\partial }^2{ϵ}_x}{\partial y^2}+\frac{{\partial }^2{ϵ}_y}{\partial x^2}\\ & \frac{{\partial }^2{\gamma }_{yz}}{\partial y\partial z}=\frac{{\partial }^2{ϵ}_y}{\partial z^2}+\frac{{\partial }^2{ϵ}_z}{\partial y^2}\\ & \frac{{\partial }^2{\gamma }_{zx}}{\partial z\partial x}=\frac{{\partial }^2{ϵ}_z}{\partial x^2}+\frac{{\partial }^2{ϵ}_x}{\partial z^2}\\ & 2\frac{{\partial }^2{ϵ}_x}{\partial y\partial z}=\frac{\partial }{\partial x}(-\frac{\partial {\gamma }_{yz}}{\partial x}+\frac{\partial {\gamma }_{zx}}{\partial y}+\frac{\partial {\gamma }_{xy}}{\partial z})\\ & 2\frac{{\partial }^2{ϵ}_y}{\partial z\partial x}=\frac{\partial }{\partial y}(\frac{\partial {\gamma }_{yz}}{\partial x}-\frac{\partial {\gamma }_{zx}}{\partial y}+\frac{\partial {\gamma }_{xy}}{\partial z})\\ & 2\frac{{\partial }^2{ϵ}_z}{\partial x\partial y}=\frac{\partial }{\partial z}(\frac{\partial {\gamma }_{yz}}{\partial x}+\frac{\partial {\gamma }_{zx}}{\partial y}-\frac{\partial {\gamma }_{xy}}{\partial z})\end{array}\}$$

这就是连续性方程，也叫变形协调条件。

2.2 平衡方程

三维弹性力学的平衡方程为：

$$\begin{array}{rl}& \frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}+f_x=0\\ & \frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}+f_y=0\\ & \frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_z}{\partial z}+f_z=0\end{array}\}$$

$f_x$、$f_y$和$f_z$为体力（外力）。在很多问题时，可以忽略体力，即：

$$\begin{array}{rl}& \frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{xz}}{\partial z}=0\\ & \frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{yz}}{\partial z}=0\\ & \frac{\partial {\tau }_{zx}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\sigma }_z}{\partial z}=0\end{array}\}$$

2.3 物理方程

对各向异性材料，其物理方程为：

1. 正轴坐标系下：

   $$\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\sigma }_3\\ {\tau }_{23}\\ {\tau }_{31}\\ {\tau }_{12}\end{array}\right]=\left[\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{21}& C_{22}& C_{23}& 0& 0& 0\\ C_{31}& C_{32}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{55}& 0\\ 0& 0& 0& 0& 0& C_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ {ϵ}_3\\ {\gamma }_{23}\\ {\gamma }_{31}\\ {\gamma }_{12}\end{array}\right]$$

   或

   $$\left[\begin{array}{c}{ϵ}_1\\ {ϵ}_2\\ {ϵ}_3\\ {\gamma }_{23}\\ {\gamma }_{31}\\ {\gamma }_{12}\end{array}\right]=\left[\begin{array}{cccccc}{S}_{11}& S_{12}& S_{13}& 0& 0& 0\\ S_{21}& S_{22}& S_{23}& 0& 0& 0\\ S_{31}& S_{32}& S_{33}& 0& 0& 0\\ 0& 0& 0& S_{44}& 0& 0\\ 0& 0& 0& 0& S_{55}& 0\\ 0& 0& 0& 0& 0& S_{66}\end{array}\right]\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\sigma }_3\\ {\tau }_{23}\\ {\tau }_{31}\\ {\tau }_{12}\end{array}\right]$$

2. 一般直角坐标系下：

   $$\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\sigma }_z\\ {\tau }_{yz}\\ {\tau }_{zx}\\ {\tau }_{xy}\end{array}\right]=\left[\begin{array}{cccccc}{\overline{C}}_{11}& {\overline{C}}_{12}& {\overline{C}}_{13}& {\overline{C}}_{14}& {\overline{C}}_{15}& {\overline{C}}_{16}\\ {\overline{C}}_{21}& {\overline{C}}_{22}& {\overline{C}}_{23}& {\overline{C}}_{24}& {\overline{C}}_{25}& {\overline{C}}_{26}\\ {\overline{C}}_{31}& {\overline{C}}_{32}& {\overline{C}}_{33}& {\overline{C}}_{34}& {\overline{C}}_{35}& {\overline{C}}_{36}\\ {\overline{C}}_{41}& {\overline{C}}_{42}& {\overline{C}}_{43}& {\overline{C}}_{44}& {\overline{C}}_{45}& {\overline{C}}_{46}\\ {\overline{C}}_{51}& {\overline{C}}_{52}& {\overline{C}}_{53}& {\overline{C}}_{54}& {\overline{C}}_{55}& {\overline{C}}_{56}\\ {\overline{C}}_{61}& {\overline{C}}_{62}& {\overline{C}}_{63}& {\overline{C}}_{64}& {\overline{C}}_{65}& {\overline{C}}_{66}\end{array}\right]\left[\begin{array}{c}{ϵ}_x\\ {ϵ}_y\\ {ϵ}_z\\ {\gamma }_{yz}\\ {\gamma }_{zx}\\ {\gamma }_{xy}\end{array}\right]$$

   或

   $$\left[\begin{array}{c}{ϵ}_x\\ {ϵ}_y\\ {ϵ}_z\\ {\gamma }_{yz}\\ {\gamma }_{zx}\\ {\gamma }_{xy}\end{array}\right]=\left[\begin{array}{cccccc}{\overline{S}}_{11}& {\overline{S}}_{12}& {\overline{S}}_{13}& {\overline{S}}_{14}& {\overline{S}}_{15}& {\overline{S}}_{16}\\ {\overline{S}}_{21}& {\overline{S}}_{22}& {\overline{S}}_{23}& {\overline{S}}_{24}& {\overline{S}}_{25}& {\overline{S}}_{26}\\ {\overline{S}}_{31}& {\overline{S}}_{32}& {\overline{S}}_{33}& {\overline{S}}_{34}& {\overline{S}}_{35}& {\overline{S}}_{36}\\ {\overline{S}}_{41}& {\overline{S}}_{42}& {\overline{S}}_{43}& {\overline{S}}_{44}& {\overline{S}}_{45}& {\overline{S}}_{46}\\ {\overline{S}}_{51}& {\overline{S}}_{52}& {\overline{S}}_{53}& {\overline{S}}_{54}& {\overline{S}}_{55}& {\overline{S}}_{56}\\ {\overline{S}}_{61}& {\overline{S}}_{62}& {\overline{S}}_{63}& {\overline{S}}_{64}& {\overline{S}}_{65}& {\overline{S}}_{66}\end{array}\right]\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\sigma }_z\\ {\tau }_{yz}\\ {\tau }_{zx}\\ {\tau }_{xy}\end{array}\right]$$

2.4 弹性力学的一般解法

弹性力学微分方程有6个应力分量、6个应变分量合3个位移分量，共15个未知函数，恰好有15个方程。

1. 在求解时，若把几何方程代入到物理方程，消去应变分量，得到位移-应力的方程；把新得到的方程代入平衡方程，消去应力分量，得到仅有位移的微分方程。这就是位移法。
2. 在求解时，若把由几何方程导出的变形协调条件代入到物理方程，消去应变分量，得到一组只含应力分量的方程；由新得到的方程与平衡方程联立，得到仅有应力的微分方程。这就是力法。
3. 也有导出同时有位移和应力的微分方程的混合法。

在解弹性力学问题时，根据求解方法和边界条件不同，可以归纳为三类基本问题：

1. 弹性体全部表面都给定了外力，要求确定弹性体内部及表面任意点上的应力和位移。其边界条件可以写作，

   $$\begin{array}{rl}& l({\sigma }_x{)}_{S_{\sigma }}+m({\tau }_{yx}{)}_{S_{\sigma }}+n({\tau }_{zx}{)}_{S_{\sigma }}={\overline{f}}_x(S_{\sigma })\\ & m({\sigma }_y{)}_{S_{\sigma }}+n({\tau }_{zy}{)}_{S_{\sigma }}+l({\tau }_{xy}{)}_{S_{\sigma }}={\overline{f}}_y(S_{\sigma })\\ & n({\sigma }_z{)}_{S_{\sigma }}+l({\tau }_{xz}{)}_{S_{\sigma }}+m({\tau }_{yz}{)}_{S_{\sigma }}={\overline{f}}_z(S_{\sigma })\end{array}\}$$

   其中$l$、$m$、$n$为$S_{\sigma }$边界的外法线与$x$、$y$和$z$轴分别的夹角余弦。应力下标$S_{\sigma }$表示应力在$S_{\sigma }$边界处。${\overline{f}}_x(S_{\sigma })$、${\overline{f}}_y(S_{\sigma })$和${\overline{f}}_z(S_{\sigma })$是$S_{\sigma }$边界处$x$、$y$和$z$方向的面力（外力）分量。
2. 弹性体在全部表面给定了位移，要求确定弹性体的内部及表面任意点上的应力和位移。其边界条件可以写作：

   $$\begin{array}{rl}& (u{)}_{S_u}=\overline{u}(S_u)\\ & (v{)}_{S_u}=\overline{v}(S_u)\\ & (w{)}_{S_u}=\overline{w}(S_u)\end{array}\}$$

   位移下标$S_u$表示应力在$S_u$边界处。$\overline{u}(S_u)$、$\overline{v}(S_u)$和$\overline{w}(S_u)$是$S_u$边界处约束位移分量。
3. 弹性体一部分表面上给定了外力，在其余表面上给定了位移，要求确定弹性体的内部及表面任意点上的应力和位移。其边界条件可以写作：

   $$\begin{array}{rl}& {\sigma }_{ij}{n}_j={\overline{f}}_i(S_{\sigma })\\ & (u{)}_{S_u}=\overline{u}(S_u)\\ & (v{)}_{S_u}=\overline{v}(S_u)\\ & (w{)}_{S_u}=\overline{w}(S_u)\end{array}\}$$

   其中应力边界条件是按照指标符号记法的。

3 复合材料梁

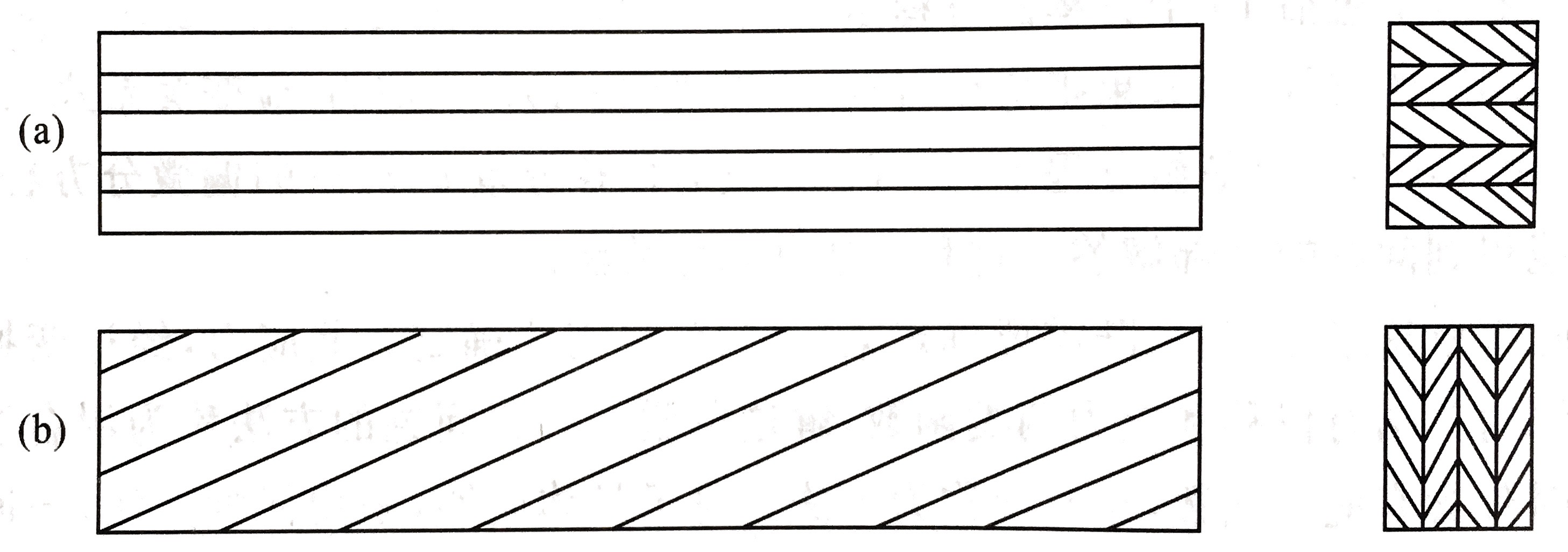
如图所示，由单层叠合成的复合梁，在承受弯矩时有两种状态。一种是(a)的层合梁，另一种是(b)的板梁。

3.1 复合材料层合梁分析

3.1.1 层合梁的抗弯刚度和应力

如图所示，由单层叠合而成的层合梁，假定载荷作用在对称面上，梁的变形满足等直线法线假设，层合梁的平截面变形后仍保持平面（${\gamma }_{zx}={\gamma }_{yz}={ϵ}_z=0$）；同时假定梁的弯曲呈柱状变形（$v=0$且$\frac{\partial u}{\partial y}=\frac{\partial w}{\partial y}=0$）。

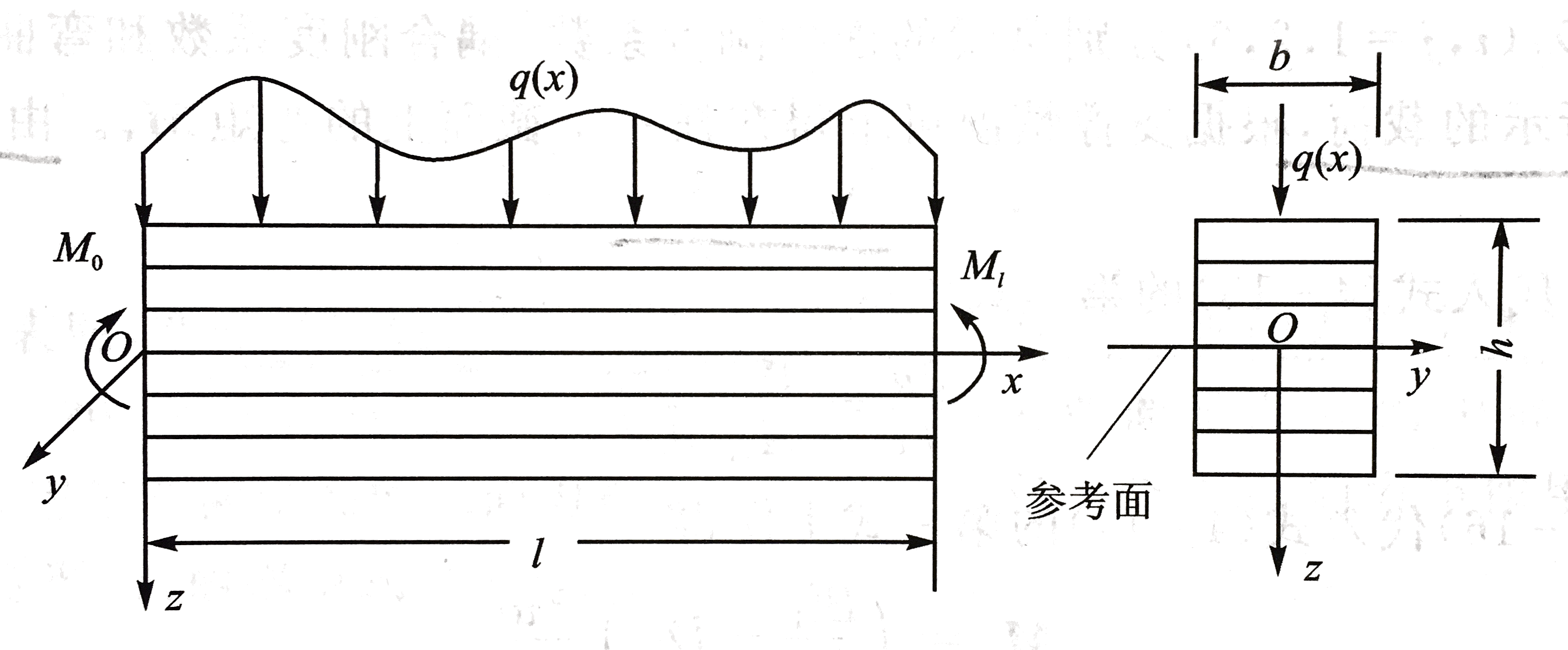
考察梁在$Oxy$平面内的变形，结合层合板的几何关系，由柱状变形假设可得层合板弯曲的几何关系：

$$\begin{array}{rl}& {ϵ}_x=\frac{\partial u_0}{\partial x}-z\frac{{\partial }^2{w}_0}{\partial x^2}\\ & {ϵ}_y=\frac{\partial v_0}{\partial y}-z\frac{{\partial }^2{w}_0}{\partial y^2}=0\\ & {\gamma }_{xy}=\frac{\partial u_0}{\partial y}+\frac{\partial v_0}{\partial x}=0\end{array}\}\text{\hspace{1em}(3.1.1.1)}$$

其中，$u_0$、$v_0$和$w_0$为参考面出的位移分量。

每个板可看成平面应力状态，对于第$k$层，按胡克定律其应力为：

$$\begin{array}{rl}& {\sigma }_x^{(k)}={\overline{Q}}_{11}^{(k)}{ϵ}_x={\overline{Q}}_{11}^{(k)}(\frac{\partial u_0}{\partial x}-z\frac{{\partial }^2{w}_0}{\partial x^2})\\ & {\sigma }_y^{(k)}={\overline{Q}}_{12}^{(k)}{ϵ}_x={\overline{Q}}_{12}^{(k)}(\frac{\partial u_0}{\partial x}-z\frac{{\partial }^2{w}_0}{\partial x^2})\\ & {\tau }_{xy}^{(k)}={\overline{Q}}_{16}^{(k)}{ϵ}_x={\overline{Q}}_{16}^{(k)}(\frac{\partial u_0}{\partial x}-z\frac{{\partial }^2{w}_0}{\partial x^2})\end{array}\}\text{\hspace{1em}(3.1.1.2)}$$

对应力沿梁高度积分，分别得到梁的内力和内力矩为：

$$\begin{array}{rl}& N_x=A_{11}\frac{\partial u_0}{\partial x}-B_{11}\frac{{\partial }^2{w}_0}{\partial x^2}\\ & N_y=A_{12}\frac{\partial u_0}{\partial x}-B_{12}\frac{{\partial }^2{w}_0}{\partial x^2}\\ & N_{xy}=A_{16}\frac{\partial u_0}{\partial x}-B_{16}\frac{{\partial }^2{w}_0}{\partial x^2}\\ & M_x=B_{11}\frac{\partial u_0}{\partial x}-D_{11}\frac{{\partial }^2{w}_0}{\partial x^2}\\ & M_y=B_{12}\frac{\partial u_0}{\partial x}-D_{12}\frac{{\partial }^2{w}_0}{\partial x^2}\\ & M_{xy}=B_{16}\frac{\partial u_0}{\partial x}-D_{16}\frac{{\partial }^2{w}_0}{\partial x^2}\end{array}\}\text{\hspace{1em}(3.1.1.3)}$$

其中$A_{ij}$、$B_{ij}$和$D_{ij}$分别是梁的面内刚度系数、耦合刚度系数和弯曲刚度系数：

$$\begin{gathered} A_{ij}=\sum _{k=1}^N{\overline{\mathbf{Q}}}_{ij}^{(k)}(z_{k+1}-z_k) \\ {B}_{ij}=\frac{1}{2}\sum _{k=1}^N{\overline{\mathbf{Q}}}_{ij}^{(k)}(z_{k+1}^2-z_k^2) \\ {D}_{ij}=\frac{1}{3}\sum _{k=1}^N{\overline{\mathbf{Q}}}_{ij}^{(k)}(z_{k+1}^3-z_k^3) \end{gathered}$$

由于面内力$N_x=0$，代入到$(3.1.1.3)$第一式得：

$$\frac{\partial u_0}{\partial x}=\frac{B_{11}}{A_{11}}\frac{{\partial }^2{w}_0}{\partial x^2}\text{\hspace{1em}(3.1.1.4)}$$

代入到$(3.1.1.3)$第四式得：

$$\frac{{\partial }^2{w}_0}{\partial x^2}=\frac{A_{11}}{B_{11}^2-A_{11}{D}_{11}}{M}_x\text{\hspace{1em}(3.1.1.5)}$$

可改写为：

$$\frac{{\partial }^2{w}_0}{\partial x^2}=\frac{M_x}{D}$$

其中，$D$被称为层合梁的抗弯刚度：

$$D=\frac{B_{11}^2-A_{11}{D}_{11}}{A_{11}}$$

当层合梁是以中面对称铺设时$B_{11}=0$，有$D=-D_{11}$。

得梁的挠度：

$$w_0(x)=\frac{1}{D}\int [\int M_x(x)\mathrm{d}x]\mathrm{d}x+C_{1}x+C_2\text{\hspace{1em}(3.1.1.6)}$$

将$(3.1.1.4)$和$(3.1.1.5)$代入到$(3.1.1.2)$中，得到部分应力：

$$\begin{array}{rl}& {\sigma }_x^{(k)}={\overline{Q}}_{11}^{(k)}\frac{A_{11}}{B_{11}^2-A_{11}{D}_{11}}(\frac{B_{11}}{A_{11}}-z)M_x\\ & {\sigma }_y^{(k)}={\overline{Q}}_{12}^{(k)}\frac{A_{11}}{B_{11}^2-A_{11}{D}_{11}}(\frac{B_{11}}{A_{11}}-z)M_x\\ & {\tau }_{xy}^{(k)}={\overline{Q}}_{16}^{(k)}\frac{A_{11}}{B_{11}^2-A_{11}{D}_{11}}(\frac{B_{11}}{A_{11}}-z)M_x\end{array}\}\text{\hspace{1em}(3.1.1.7)}$$

若将$(3.1.1.4)$和$(3.1.1.5)$代入到$(3.1.1.3)$，也可求得部分内力和内力矩关系：

$$\begin{array}{rl}& N_x=0\\ & N_y=\frac{A_{12}{B}_{11}-A_{11}{B}_{12}}{B_{11}^2-A_{11}{D}_{11}}{M}_x\\ & N_{xy}=\frac{A_{16}{B}_{11}-A_{11}{B}_{16}}{B_{11}^2-A_{11}{D}_{11}}{M}_x\\ & M_x=M_x\\ & M_y=\frac{B_{11}{B}_{12}-A_{11}{D}_{12}}{B_{11}^2-A_{11}{D}_{11}}{M}_x\\ & M_{xy}=\frac{B_{11}{B}_{16}-A_{11}{D}_{16}}{B_{11}^2-A_{11}{D}_{11}}{M}_x\end{array}\}$$

可以看出，在柱状弯曲状态下，内力$N_y$、$N_{xy}$、$M_y$和$M_{xy}$均不为零。即：要使层合梁形成柱状弯曲，除了加载弯矩和剪力外，还要在边界处提供上述内力方向的外载荷。

3.1.2 层合梁的中性面位置

对于非对称铺层的层合梁，中性面并不是几何中面。如图所示，非对称层合梁几何中面上作用一轴向力$N$，

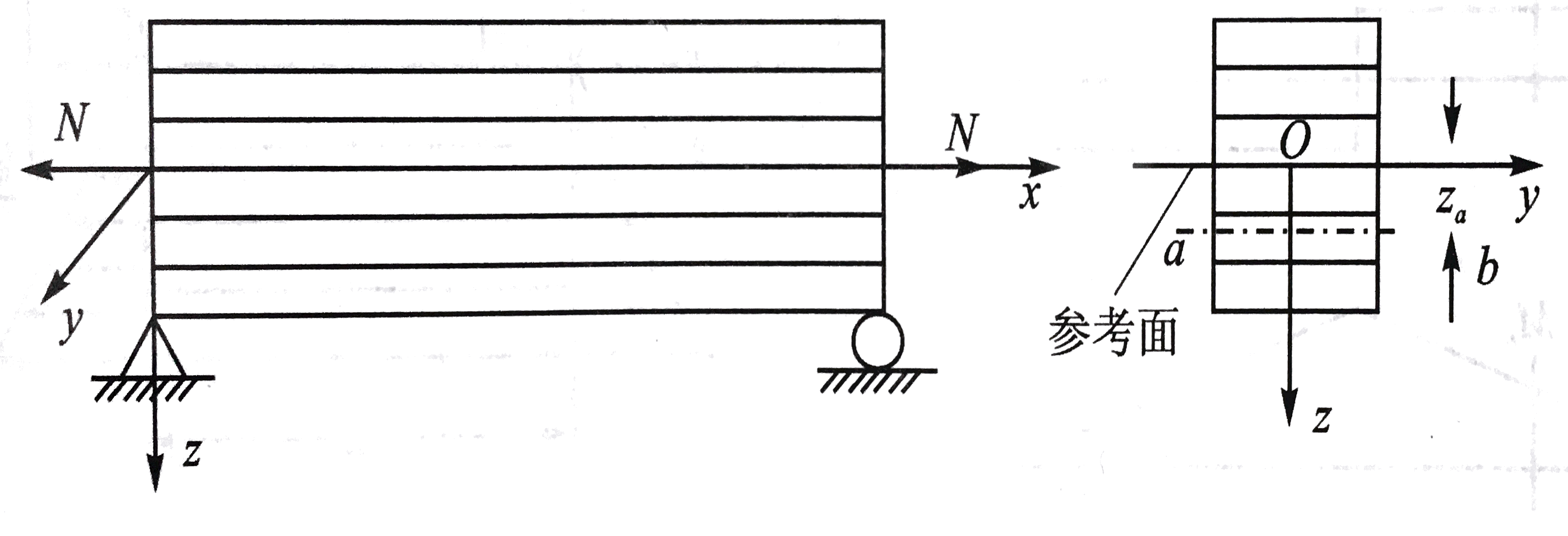
沿几何中面各店的内力和内力矩分别为$N_x^0=N$和$M_x^0=0$，带入到$(3.1.1.3)$的第一式和第四式中：

$$\begin{array}{rl}& \frac{\partial u_0}{\partial x}=\frac{D_{11}}{A_{11}{D}_{11}-B_{11}^2}N\\ & \frac{{\partial }^2{w}_0}{\partial x^2}=\frac{B_{11}}{A_{11}{D}_{11}-B_{11}^2}N\end{array}\}\text{\hspace{1em}(3.1.2.1)}$$

另一方面，假定中性面是距几何中面为$z_a$的$ab$面，则按中性面的定义，曲率可表示为：

$$\frac{{\partial }^2{w}_0}{\partial x^2}=\frac{A_{11}}{A_{11}{D}_{11}-B_{11}^2}N{z}_a\text{\hspace{1em}(3.1.2.2)}$$

将$(3.1.2.1)$的第二式和$(3.1.2.2)$对比，得中性面的位置：

$$z_a=\frac{B_{11}}{A_{11}}$$

3.1.3 层合梁的剪应力

除纯弯梁以外，通产在横向载荷作用下，将产生$Oxy$面内剪应力。如图所示，在集中载荷作用下简支梁的剪力图、弯矩图以及微元体应力内力分布图。

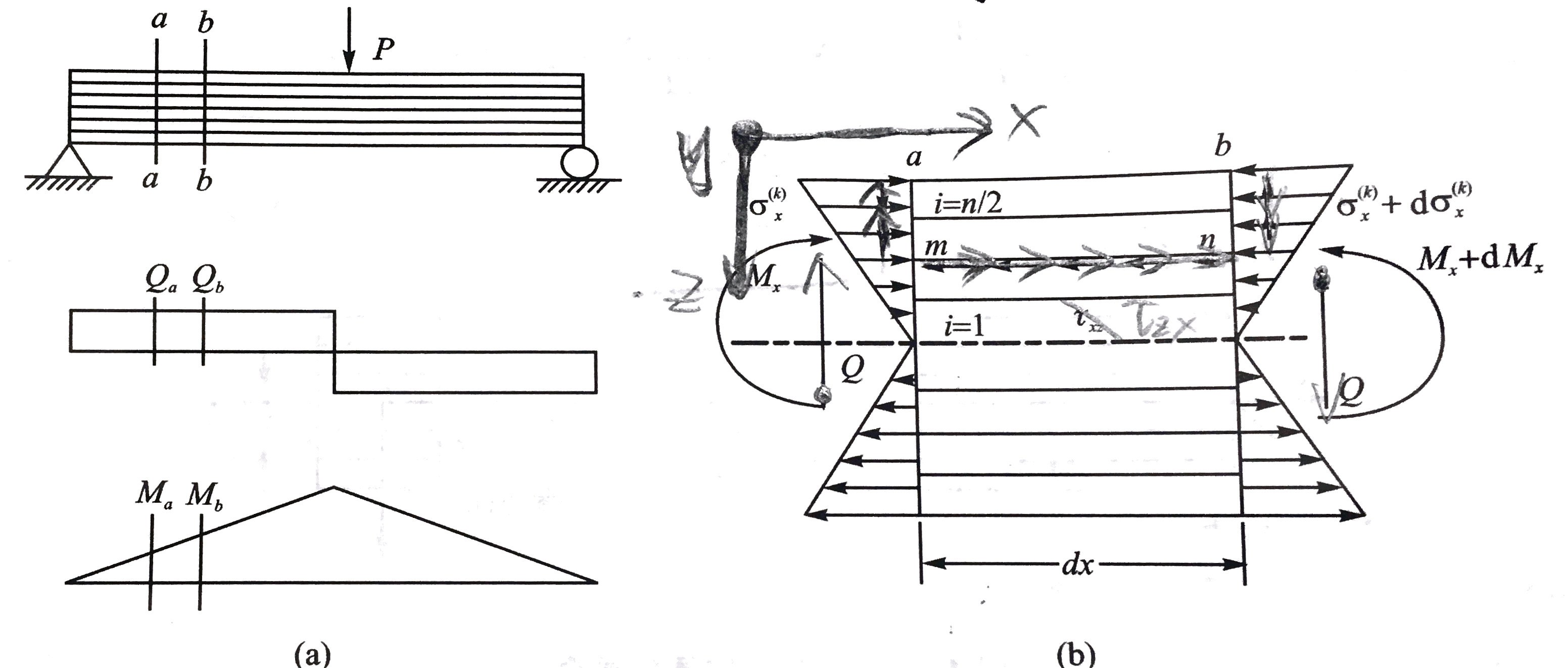
注意：为了使弹性力学和材料力学的梁的剪力、弯矩正方向一致，按如图所示放置坐标系。即：$x$轴为梁的长度方向，向右为正；$y$轴为梁的宽度方向，向外为正，$z$轴为梁的厚度方向，向下为正。
与各向同性梁一样，在层合梁的横截面将存在与剪力方向平行的剪应力${\tau }_{xz}$，其内部也存在平行于横截面法线的剪应力${\tau }_{zx}$。在梁的$a-a$和$b-b$处截出长为$\mathrm{d}x$的一段微元体。再截取相距参考面$z_i$的$m-n$截面以上的部分$amnb$，画出其微元应力分量。

微元体在$x$方向平衡，即$\sum X=0$，设梁宽为$b$，则有：

$${\int }_{z_i}^{\frac{h}{2}}{\sigma }_x^{(k)}b\mathrm{d}z+{\tau }_{zx}^{(k)}b\mathrm{d}x={\int }_{z_i}^{\frac{h}{2}}({\sigma }_x^{(k)}+\mathrm{d}{\sigma }_x^{(k)})b\mathrm{d}z$$

从而：

$${\tau }_{zx}^{(k)}=\frac{1}{\mathrm{d}x}{\int }_{z_i}^{\frac{h}{2}}\mathrm{d}{\sigma }_x^{(k)}\mathrm{d}z$$

将$(3.1.1.7)$的第一式代入上式，得：

$${\tau }_{zx}^{(k)}=\frac{A_{11}}{B_{11}^2-A_{11}{D}_{11}}\frac{\mathrm{d}{M}_x}{\mathrm{d}x}[\frac{B_{11}}{A_{11}}{\int }_{z_i}^{\frac{h}{2}}{\overline{Q}}_{11}^{(k)}\mathrm{d}z-{\int }_{z_i}^{\frac{h}{2}}{\overline{Q}}_{11}^{(k)}z\mathrm{d}z]$$

对于对称层合梁，$B_{11}=0$，于是其剪应力可化简为：

$${\tau }_{zx}^{(k)}=\frac{Q_x}{D_{11}}{\int }_{z_i}^{\frac{h}{2}}{\overline{Q}}_{11}^{(k)}z\mathrm{d}z$$

注意到：

$${\int }_{z_i}^{\frac{h}{2}}{\overline{Q}}_{11}^{(k)}z\mathrm{d}z=\sum _{i=k}^{n/2}{\overline{Q}}_{11}^{(k)}{\int }_{z_k}^{z_{k+1}}z\mathrm{d}z=\sum _{i=k}^{n/2}{\overline{Q}}_{11}^{(k)}{S}_k$$

其中$S_k$为$z_k$处单位宽度层合梁对于参考轴的静矩：

$$S_k=\frac{(z_{k+1}+z_k)(z_{k+1}-z_k)}{2}$$

于是对称层合梁剪应力公式为：

$${\tau }_{zx}^{(k)}=\frac{Q_x}{D_{11}}\sum _{i=k}^{n/2}{\overline{Q}}_{11}^{(k)}{S}_k\text{\hspace{1em}(3.1.3.1)}$$

3.2 复合材料板梁分析

板梁的高度较大而宽度较小，与平板的面内受力状态相似，通常是处于平面应力状态。
如图所示，一段受有集中载荷一段固定的悬臂梁。

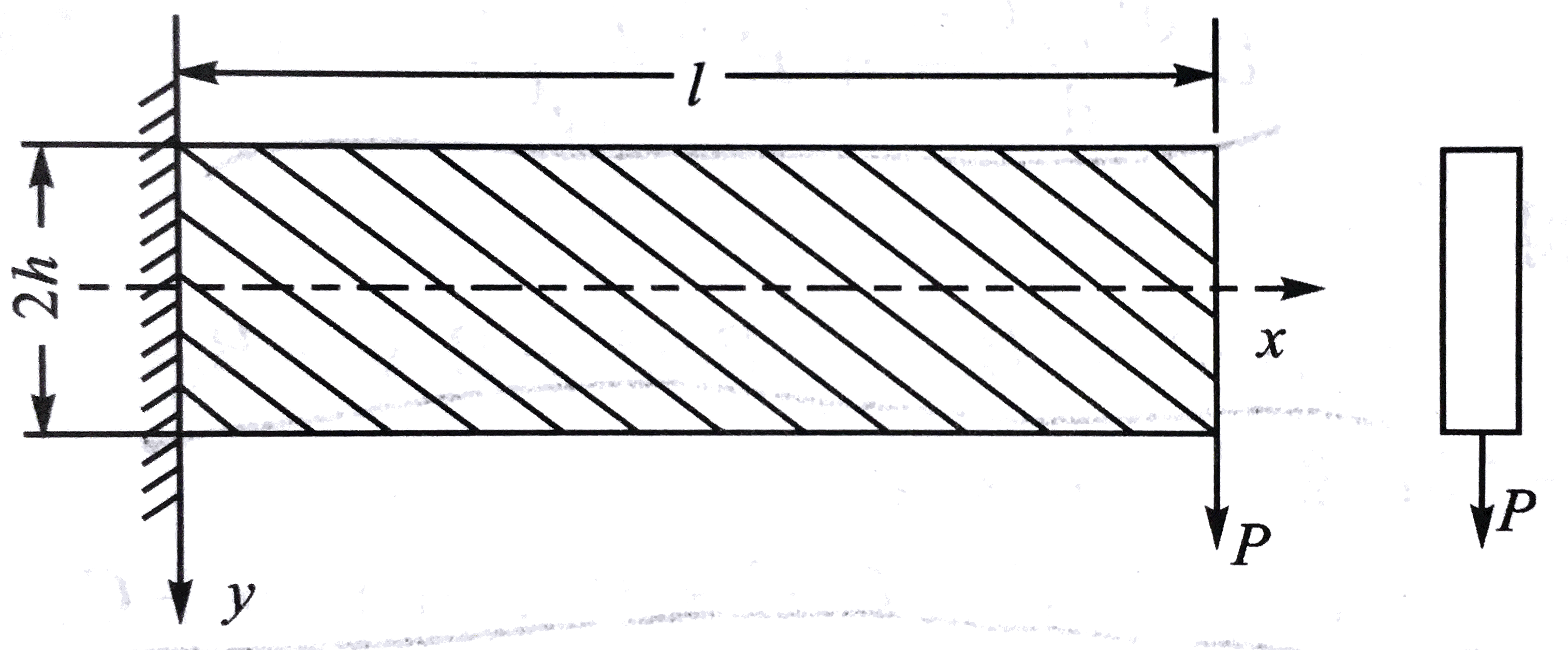
为了计算简便，此时板梁为单层板，选取的坐标系不与材料主轴重合。

按照力法求解弹性力学方程。体力视为零，设应力函数为$F(x,y)$，则：

$$\begin{array}{rl}& {\sigma }_x=\frac{{\partial }^{2}F(x,y)}{\partial y^2}\\ & {\sigma }_y=\frac{{\partial }^{2}F(x,y)}{\partial x^2}\\ & {\tau }_{xy}=-\frac{{\partial }^{2}F(x,y)}{\partial x\partial y}\end{array}\}\text{\hspace{1em}(3.2.1)}$$

下面按照半逆解法求解应力函数。

由于上下边界无任何外力，则${\sigma }_y=0$，即：

$${\sigma }_y=\frac{{\partial }^{2}F(x,y)}{\partial x^2}=0$$

将上面方程对$x$作两次积分：

$$F(x,y)=x{f}_1(y)+f_2(y)\text{\hspace{1em}(3.2.2)}$$

平面应力状态的物理方程为：

$$\left[\begin{array}{c}{ϵ}_x\\ {ϵ}_y\\ {\gamma }_{xy}\end{array}\right]=\left[\begin{array}{ccc}{\overline{S}}_{11}& {\overline{S}}_{12}& {\overline{S}}_{16}\\ {\overline{S}}_{21}& {\overline{S}}_{22}& {\overline{S}}_{26}\\ {\overline{S}}_{61}& {\overline{S}}_{62}& {\overline{S}}_{66}\end{array}\right]\left[\begin{array}{c}{\sigma }_x\\ {\sigma }_y\\ {\tau }_{xy}\end{array}\right]\text{\hspace{1em}(3.2.3)}$$

变形协调方程为：

$$\frac{{\partial }^2{ϵ}_x}{\partial y^2}+\frac{{\partial }^2{ϵ}_y}{\partial x^2}=\frac{{\partial }^2{\gamma }_{xy}}{\partial x\partial y}\text{\hspace{1em}(3.2.4)}$$

将$(3.2.1)$代入到$(3.2.3)$，再代入到$(3.2.4)$得平面问题的基本方程：

$$\begin{gathered} {\overline{S}}_{22}\frac{{\partial }^{4}F(x,y)}{\partial x^4}-2{\overline{S}}_{26}\frac{{\partial }^{4}F(x,y)}{\partial x^3\partial y}+(2{\overline{S}}_{12}+{\overline{S}}_{66})\frac{{\partial }^{4}F(x,y)}{\partial x^2\partial y^2}- \\ 2{\overline{S}}_{16}\frac{{\partial }^{4}F(x,y)}{\partial x\partial y^3}+{\overline{S}}_{11}\frac{{\partial }^{4}F(x,y)}{\partial y^4}=0\text{\hspace{1em}(3.2.5)} \end{gathered}$$

再将$(3.2.2)$代入到上式，同时令$D=-2{\overline{S}}_{16}$，$E={\overline{S}}_{22}$得：

$$D\frac{{\mathrm{d}}^3{f}_1(y)}{\mathrm{d}{y}^3}+Ex\frac{{\mathrm{d}}^4{f}_1(y)}{\mathrm{d}{y}^4}+E\frac{{\mathrm{d}}^4{f}_2(y)}{\mathrm{d}{y}^4}=0$$

要使上述方程对任意$x$均成立，应有：

$$\begin{array}{rl}& \frac{{\mathrm{d}}^4{f}_1(y)}{\mathrm{d}{y}^4}=0\\ & D\frac{{\mathrm{d}}^3{f}_1(y)}{\mathrm{d}{y}^3}+E\frac{{\mathrm{d}}^4{f}_2(y)}{\mathrm{d}{y}^4}=0\end{array}\}\text{\hspace{1em}(3.2.6)}$$

由上式的第一式得：

$$f_1(y)=B_1{y}^3+B_2{y}^2+B_{3}y+B_4$$

将上式代入到$(3.2.6)$第二式中：

$$f_2(y)=C_1{y}^4+C_2{y}^3+C_3{y}^2+C_{4}y+C_5$$

将上面两式回代到$(3.2.2)$中，并略去不影响应力分布的一次项及常数项：

$$F(x,y)=B_{1}x{y}^3+B_{2}x{y}^2+B_{3}xy+C_1{y}^4+C_2{y}^3+C_3{y}^2\text{\hspace{1em}(3.2.7)}$$

模型中有以下边界条件：

1. 在$y=\pm h$处（上下面边界）无面力：$({\sigma }_y{)}_{y=\pm h}=({\tau }_{xy}{)}_{y=\pm h}=0$；
2. 在$y=l$处（自由端）轴向力为零：$N={\int }_{-h}^{+h}({\sigma }_x{)}_{x=l}\mathrm{d}y=0$；
3. 在$y=l$处（自由端）受已知剪力：$P={\int }_{-h}^{+h}({\tau }_{xy}{)}_{x=l}\mathrm{d}y$；
4. 在$y=l$处（自由端）弯矩为零：$M={\int }_{-h}^{+h}({\sigma }_x{)}_{x=l}y\mathrm{d}y=0$。

将条件1的$({\tau }_{xy}{)}_{y=\pm h}=0$代入到$(3.2.1)$的第三式和$(3.2.7)$得：

$$-3B_1{h}^2+2B_{2}h+B_3=-3B_1{h}^2-2B_{2}h+B_3$$

则$B_2=0$。于是可把$(3.2.7)$写成：

$$F(x,y)=A_{1}xy+A_2{y}^2+A_3{y}^3+A_{4}x{y}^3+A_5{y}^4\text{\hspace{1em}(3.2.8)}$$

将上式代入$(3.2.1)$得：

$$\begin{array}{rl}& {\sigma }_x=2A_2+6A_{3}y+6A_{4}xy+12A_5{y}^2\\ & {\sigma }_y=0\\ & {\tau }_{xy}=-A_1-3A_4{y}^2\end{array}\}\text{\hspace{1em}(3.2.9)}$$

将上式代入边界条件得：

$$\begin{gathered} A_1+3A_4{h}^2=0 \\ {A}_2+2A_5{h}^2=0 \\ {A}_1+A_4{h}^2=-\frac{P}{2h} \\ {A}_3+A_{4}l=0 \end{gathered}$$

除此之外，将$(3.2.8)$代入到$(3.2.5)$中，得：

$$A_4=2\frac{{\overline{S}}_{11}}{{\overline{S}}_{16}}{A}_5$$

由以上五个方程解得：

$$A_1=-\frac{3P}{4h},A_2=-\frac{P}{4h}\frac{{\overline{S}}_{16}}{{\overline{S}}_{11}},A_3=\frac{Pl}{4h^3},A_4=\frac{P}{4h^3},A_5=\frac{P}{8h^3}\frac{{\overline{S}}_{16}}{{\overline{S}}_{11}}$$

将上述解代入$(3.2.9)$得梁的应力：

$$\begin{array}{rl}& {\sigma }_x=\frac{3}{2}\frac{P}{h^3}(l-x)y-\frac{{\overline{S}}_{16}}{2{\overline{S}}_{11}}\frac{P}{h^3}(h^2-3y^2)\\ & {\sigma }_y=0\\ & {\tau }_{xy}=\frac{3}{4}\frac{P}{h^3}(h^2-y^2)\end{array}\}\text{\hspace{1em}(3.2.10)}$$

于是其分布情况如图所示：

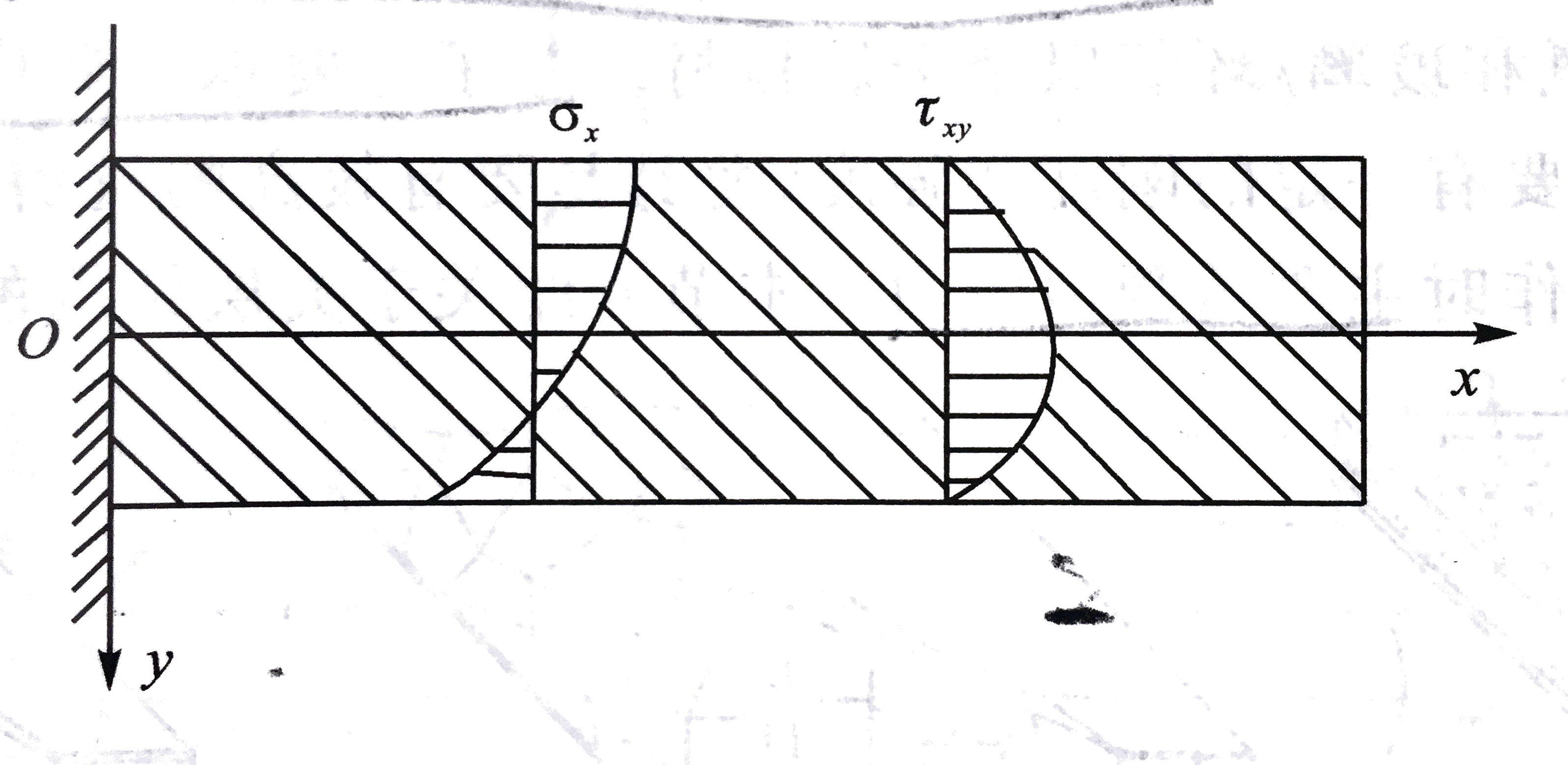
由此可见，对于$x$方向拉压与$xy$面剪切耦合的单层复合材料板梁（${\overline{S}}_{16}\ne 0$），弯曲时${\sigma }_x$不是关于几何中面对称分布的；但${\tau }_{xy}$与各向同性梁一样，沿高度呈抛物线分布。

将上面的应力解代入物理方程，再代入到几何方程得位移函数：

$$\begin{array}{rl}& u=\frac{P}{4h^3}[-3{\overline{S}}_{11}(2l-x)xy+{\overline{S}}_{16}(h^2-3y^2)x+\\ & (\frac{2{\overline{S}}_{16}^2}{{\overline{S}}_{11}}-{\overline{S}}_{12}-{\overline{S}}_{66})y^3-3{\overline{S}}_{16}l{y}^2]\\ & v=\frac{P}{4h^3}[-2{\overline{S}}_{12}(l-x)y^2-\frac{2{\overline{S}}_{16}}{{\overline{S}}_{11}}(h^2-y^2)y+{\overline{S}}_{26}(3h^2-y^2)y+\\ & {\overline{S}}_{11}(3l-x)x^2+(3{\overline{S}}_{66}-\frac{2{\overline{S}}_{16}^2}{{\overline{S}}_{11}})h^{2}x]\end{array}\}\text{\hspace{1em}(3.2.11)}$$

梁中心线的最大挠度，即在$x=l$、$y=0$处的$v$为：

$$v_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{P{l}^3}{4h^3}[2{\overline{S}}_{11}+\frac{h^2}{l^2}(3{\overline{S}}_{66}-\frac{{\overline{S}}_{16}}{{\overline{S}}_{11}})]\text{\hspace{1em}(3.2.12)}$$

4 夹层结构分析

板结构在承受弯矩时，远离中面的层可以提供较大的抗弯刚度。因此在设计承弯结构时把弹性模量大、强度高的材料配置在远离中面的部位，中面附近受力较小，可使用强度和模量较低的材料。夹层板和夹层梁就是这类结构的典型例子。

如图所示，夹层结构通常由三部分组成，最外层是面板，也被称蒙皮；中间是芯材，常用的有泡沫塑料、金属或非金属材料制成的蜂窝和波纹板；将面板和芯材连接在一起的是胶结层。

夹层结构的面板主要承受弯曲变形引起的正应力。芯子主要承受剪应力。胶结层主要承受剪应力。

4.1 夹层板分析基础

对夹层板做如下假设：

1. 薄板面只承受面内应力${\sigma }_x$、${\sigma }_y$和${\tau }_{xy}$，为平面应力状态；
2. 由于芯材较软，故忽略夹心平行于$Oxy$面内应力分布，只承受沿厚度均匀分布横向剪应力，其应力状态是${\sigma }_x={\sigma }_y={\tau }_{xy}=0$，${\tau }_{xz}\ne 0$和${\tau }_{yz}\ne 0$；
3. 在夹芯和面板中，应力分量${\sigma }_z$很小，即假定${\sigma }_z=0$，同时假设${ϵ}_z=0$。

如图所示，在面板为层合板、芯材为各向同性材料构成的夹层板上，设立直角坐标系$Oxyz$，$xy$平面为芯材几何中面，$z$轴向下。其上作用弯矩扭矩$M_x$、$M_y$和$M_{xy}$，以及剪力$Q_{yz}$和$Q_{xz}$。

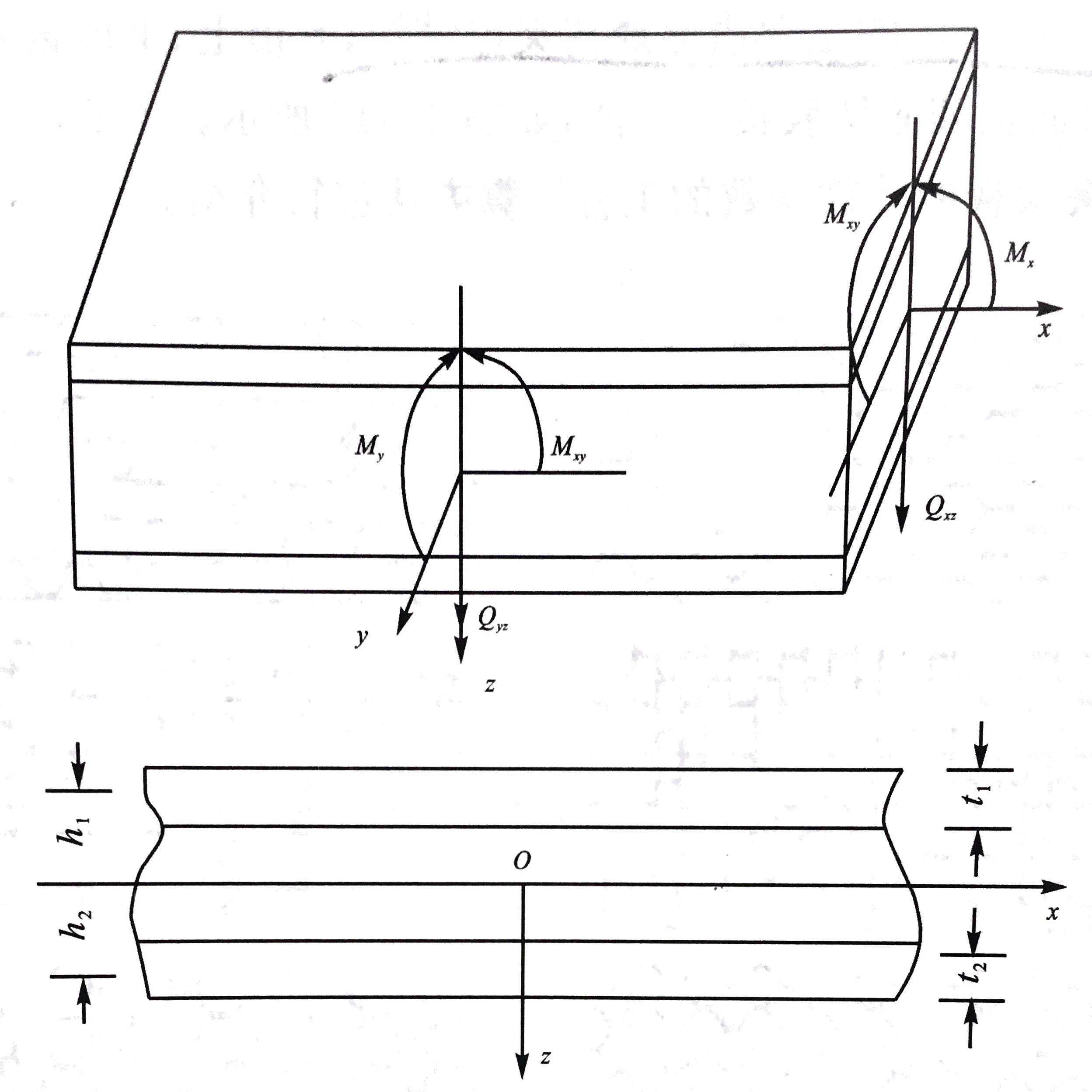
1. 芯材：
   由假设2得：

   $$\frac{\partial {\tau }_{yz}}{\partial z}=0,\frac{\partial {\tau }_{xz}}{\partial z}=0$$

   设芯材厚度为$h_c$。于是

   $$\begin{array}{rl}& {\tau }_{yz}=\frac{Q_{yz}}{h_c}\\ & {\tau }_{xz}=\frac{Q_{xz}}{h_c}\end{array}\}$$

   芯材的剪切模量为$G_c$，代入物理方程，结合几何方程得：

   $$\begin{array}{rl}& {\gamma }_{xz}=\frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}=\frac{Q_{xz}}{G_c{h}_c}\\ & {\gamma }_{yz}=\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}=\frac{Q_{yz}}{G_c{h}_c}\end{array}\}$$

   由${ϵ}_z=0$得$w=w_0(x,y)$。令$C=G_c{h}_c$，将上式对$z$积分得：

   $$\begin{array}{rl}& u=u_0(x,y)-z(\frac{\partial w_0(x,y)}{\partial x}-\frac{Q_{xz}}{C})\\ & v=v_0(x,y)-z(\frac{\partial w_0(x,y)}{\partial y}-\frac{Q_{yz}}{C})\end{array}\}$$

   令：

   $$\begin{array}{rl}& {\varphi }_x=\frac{\partial w_0}{\partial x}-\frac{Q_{xz}}{C}\\ & {\varphi }_y=\frac{\partial w_0}{\partial y}-\frac{Q_{yz}}{C}\end{array}\}\text{\hspace{1em}(4.1.1)}$$

   结合$w$的函数，得芯材的位移函数：

   $$\begin{array}{rl}& u=u_0-z{\varphi }_x\\ & v=v_0-z{\varphi }_y\\ & w=w_0\end{array}\}\text{\hspace{1em}(4.1.2)}$$

   其中$-h_c/2\le z\le h_c/2$。

   可以看出，${\varphi }_x$和${\varphi }_y$是芯材的转角，$u_0$和$v_0$是参考面的面内位移。

2. 板面：
   以下面板为例，由于面板为平面应力状态（${\tau }_{yz}={\tau }_{xz}={\sigma }_z=0$），代入单层的偏轴物理方程得：${\gamma }_{xz}={\gamma }_{yz}=0$，又已假设${ϵ}_z=0$，则可用经典层合板理论分析面板。

   取直角坐标系$O_{2}xy{z}_2$，它是由坐标系$Oxyz$向下平移到下面板的几何中面形成的，于是

   $$z_2=z-h_2\text{\hspace{1em}(4.1.3)}$$

   由经典层合板理论得：

   $$\begin{array}{rl}& u=u_{0_2}(x,y)-z_2\frac{\partial w_{0_2}(x,y)}{\partial x}\\ & v=v_{0_2}(x,y)-z_2\frac{\partial w_{0_2}(x,y)}{\partial y}\\ & w=w_{0_2}(x,y)\end{array}\}$$

   其中$-t_2/2\le z_2\le t_2/2$，$t_2$为下面板的厚度，则有：

   $$h_c/2=h_2-t_2/2\text{\hspace{1em}(4.1.4)}$$

   胶结层很薄，在芯材和面板接触面上视作没有相对滑动。所以位移函数$u$、$v$和$w$在接触面处连续。又由于$w_0(w,y)$与$w_{0_2}(x,y)$与$z$无关，即二者不沿厚度变化，所以$w_{0_2}=w_0$。则上式可写为：

   $$\begin{array}{rl}& u=u_{0_2}(x,y)-z_2\frac{\partial w_0(x,y)}{\partial x}\\ & v=v_{0_2}(x,y)-z_2\frac{\partial w_0(x,y)}{\partial y}\\ & w=w_0(x,y)\end{array}\}\text{\hspace{1em}(4.1.5)}$$

   在芯材和下面板接触面上，$z=h_c/2$、$z_2=-t_2/2$。代入到$(4.1.2)$和$(4.1.5)$中，此时两组函数表示相同的点的位移情况，二者应该相等：

   $$\begin{gathered} u_0-\frac{h_c}{2}{\varphi }_x=u_{0_2}+\frac{t_2}{2}\frac{\partial w_0}{\partial x} \\ {v}_0-\frac{h_c}{2}{\varphi }_y=v_{0_2}+\frac{t_2}{2}\frac{\partial w_0}{\partial y} \end{gathered}$$

   即得到下板面的中面位移：

   $$\begin{array}{rl}& u_{0_2}=u_0-\frac{h_c}{2}{\varphi }_x-\frac{t_2}{2}\frac{\partial w_0}{\partial x}\\ & v_{0_2}=v_0-\frac{h_c}{2}{\varphi }_y-\frac{t_2}{2}\frac{\partial w_0}{\partial y}\\ & w_{0_2}=w_0\end{array}\}\text{\hspace{1em}(4.1.6)}$$

   将上式代入到$(4.1.5)$中：

   $$\begin{array}{rl}& u=u_0-\frac{h_c}{2}{\varphi }_x-\frac{t_2}{2}\frac{\partial w_0}{\partial x}-z_2\frac{\partial w_0}{\partial x}\\ & v=v_0-\frac{h_c}{2}{\varphi }_y-\frac{t_2}{2}\frac{\partial w_0}{\partial y}-z_2\frac{\partial w_0}{\partial y}\\ & w=w_0(x,y)\end{array}\}$$

   由$(4.1.3)$和$(4.1.4)$得：$z_2=z-t_2/2-h_c/2$。将其代入上式中，并注意到$(4.1.1)$得：

   $$\begin{array}{rl}& u=u_0+\frac{h_c}{2}\frac{Q_{xz}}{C}-z\frac{\partial w_0}{\partial x}\\ & v=v_0+\frac{h_c}{2}\frac{Q_{yz}}{C}-z\frac{\partial w_0}{\partial y}\\ & w=w_0\end{array}\}\text{\hspace{1em}(4.1.7)}$$

   其中$h_c/2\le z\le h_c/2+t_2$。

   同理得上板面的中面位移为：

   $$\begin{array}{rl}& u_{0_1}=u_0+\frac{h_c}{2}{\varphi }_x+\frac{t_2}{2}\frac{\partial w_0}{\partial x}\\ & v_{0_1}=v_0+\frac{h_c}{2}{\varphi }_y+\frac{t_2}{2}\frac{\partial w_0}{\partial y}\\ & w_{0_1}=w_0\end{array}\}\text{\hspace{1em}(4.1.8)}$$

   上板面的位移函数为：

   $$\begin{array}{rl}& u=u_0-\frac{h_c}{2}\frac{Q_{xz}}{C}-z\frac{\partial w_0}{\partial x}\\ & v=v_0-\frac{h_c}{2}\frac{Q_{yz}}{C}-z\frac{\partial w_0}{\partial y}\\ & w=w_0\end{array}\}\text{\hspace{1em}(4.1.9)}$$

   其中$-h_c/2\le z\le -h_c/2-t_2$。

综合$(4.1.2)$、$(4.1.7)$和$(4.1.9)$得整个夹层板的位移函数：

$$\begin{array}{rl}& u=\{\begin{array}{l}{u}_0-\frac{h_c}{2}\frac{Q_{xz}}{C}-z\frac{\partial w_0}{\partial x}(-h_c/2-t_1/2\le z\le -h_c/2)\\ u_0-z{\varphi }_x(-h_c/2\le z\le h_c/2)\\ u_0+\frac{h_c}{2}\frac{Q_{xz}}{C}-z\frac{\partial w_0}{\partial x}(h_c/2\le z\le h_c/2+t_2/2)\end{array}\\ & v=\{\begin{array}{l}{v}_0-\frac{h_c}{2}\frac{Q_{yz}}{C}-z\frac{\partial w_0}{\partial y}(-h_c/2-t_1/2\le z\le -h_c/2)\\ v_0-z{\varphi }_y(-h_c/2\le z\le h_c/2)\\ v_0+\frac{h_c}{2}\frac{Q_{yz}}{C}-z\frac{\partial w_0}{\partial y}(h_c/2\le z\le h_c/2+t_2/2)\end{array}\\ & w=w_0\end{array}\}\text{\hspace{1em}(4.1.10)}$$

上下面板的中面位移为：

$$\begin{array}{rl}& u_{0_i}=u_0-\frac{h_c}{2}{\varphi }_x\pm \frac{t_i}{2}\frac{\partial w_0}{\partial x}\\ & v_{0_i}=v_0-\frac{h_c}{2}{\varphi }_y\pm \frac{t_i}{2}\frac{\partial w_0}{\partial y}\\ & w_{0_i}=w_0\end{array}\}\text{\hspace{1em}(4.1.11)}$$

$i=1,2$分别表示上、下面的量。当$i=1$时，$\pm$号取$-$号；当$i=2$时，$\pm$号取$+$号。

4.2 蜂窝夹层结构的工程计算

航空航天器结构设计中常用的夹层结构是蜂窝芯层。目前工程中比较广泛应用的是六边形蜂窝夹层结构。

4.2.1 蜂窝夹层结构的密度计算

如图所示蜂窝夹层的结构：

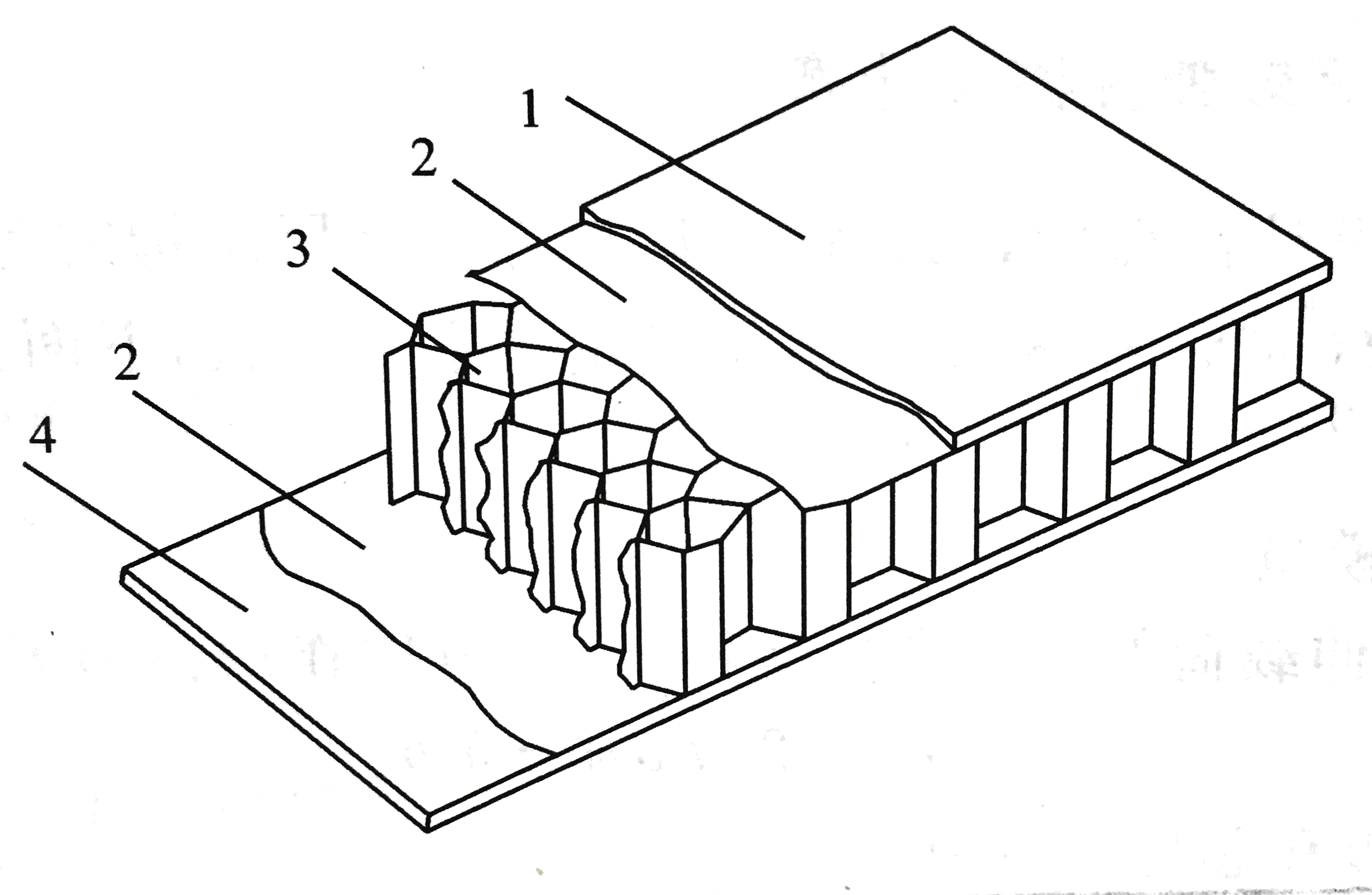
上、下面板的厚度分别为$t_1$和$t_2$，密度分别为${\rho }_1$和${\rho }_2$；胶结层的厚度为$t_p$，密度为${\rho }_p$;蜂窝夹层结构整体的长度、宽度和高度分别为$a$、$b$和$h$。于是蜂窝芯高度为：

$$h_c=h-(t_1+t_2+2t_p)$$

于是蜂窝夹层结构的密度为：

$$\begin{gathered} \rho =\frac{ab{t}_1{\rho }_1+ab{t}_2{\rho }_2+2ab{t}_p{\rho }_p+ab{h}_c{\rho }_c}{abh}= \\ \frac{t_1}{h}{\rho }_1+\frac{t_2}{h}{\rho }_2+2\frac{t_p}{h}{\rho }_p+(1-\frac{t_1+t_2+2t_p}{h}){\rho }_c \end{gathered}$$

其中，${\rho }_c$为蜂窝芯子的等效密度。

通常蜂窝夹层结构的上、下面板厚度相同，且由同样的层合板制成，即$t_1=t_2=t_f$，${\rho }_1={\rho }_2={\rho }_f$，而蜂窝芯的密度${\rho }_c$比${\rho }_f$要小很多，且$t_p$很小，故$\frac{2t_p}{h}{\rho }_c$项可以略去，于是上式简化为：

$$\rho =\frac{2t_f{\rho }_f}{h}+\frac{2t_p{\rho }_p}{h}+(1-\frac{2t_f}{h}){\rho }_c\text{\hspace{1em}(4.2.1.1)}$$

下面计算蜂窝芯材的等效密度。

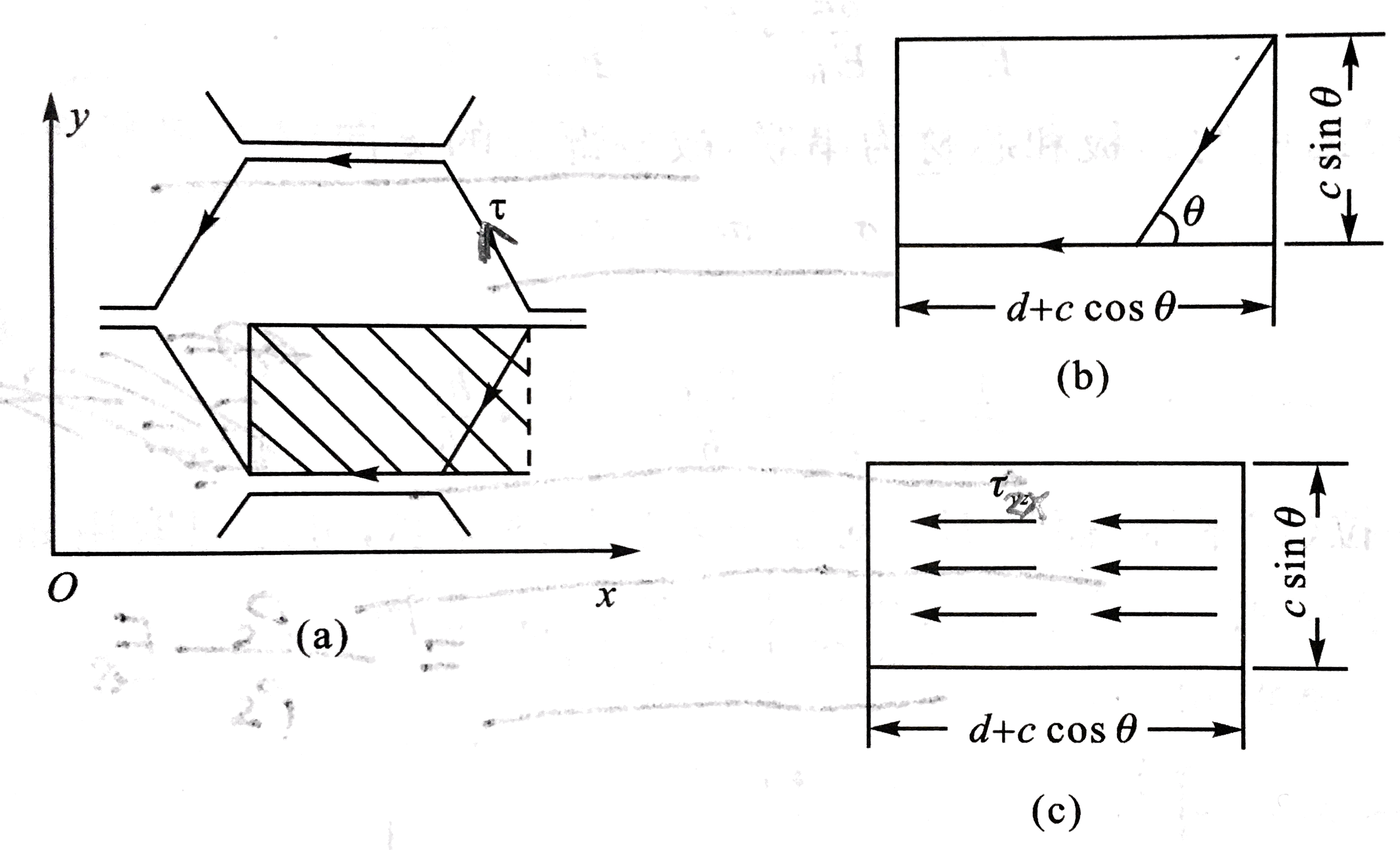
如图所示，取出六边形蜂窝芯中阴影部分的矩形，作为考虑密度的基本单元。

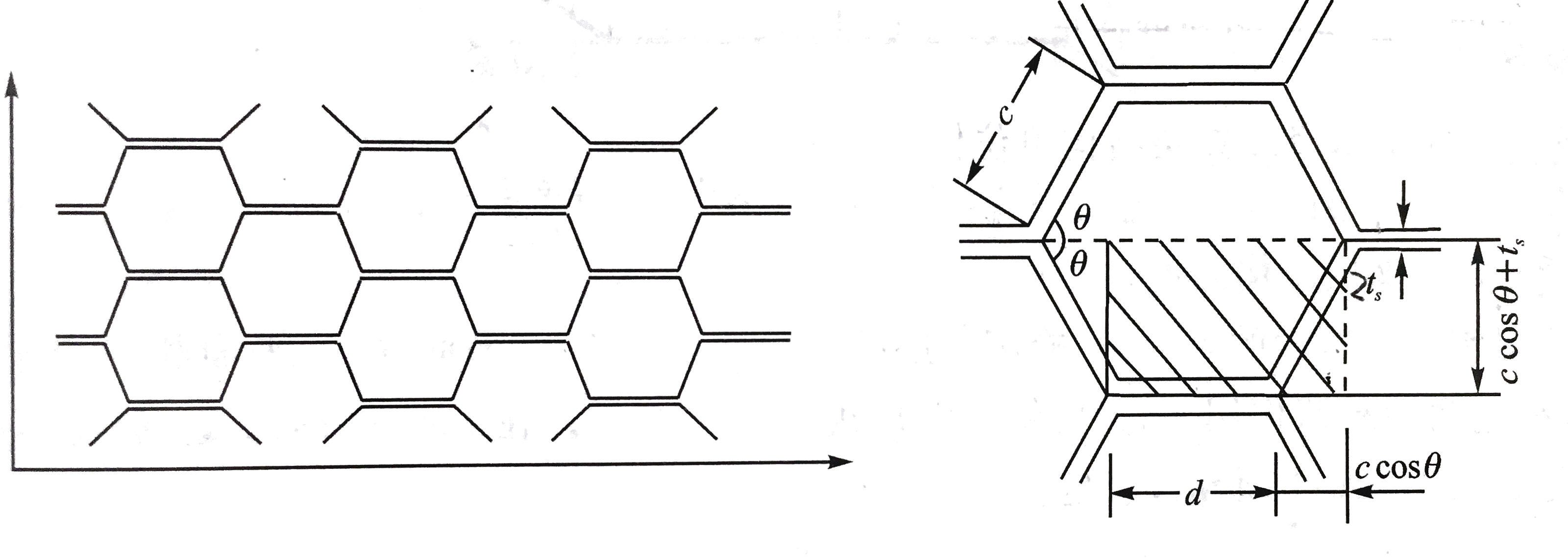
蜂窝壁材料密度为${\rho }_s$。按图的尺寸，蜂窝芯材的密度为：

$${\rho }_c=\frac{(d+c)t_s{h}_c{\rho }_s}{(d+c\cos \theta )(c\cos \theta +t_s)}$$

正六边形蜂窝芯的$\theta =60^{\circ }$，于是上式变为：

$${\rho }_c=1.54{\rho }_s\frac{t_s}{c}\text{\hspace{1em}(4.2.1.2)}$$

将上式代入到$(4.2.1.1)$中，得蜂窝夹层结构的密度为：

$$\rho =\frac{2t_f{\rho }_f}{h}+\frac{4t_p{\rho }_p}{h}+1.54\frac{t_s}{c}(1-\frac{2t_f}{h}){\rho }_s\text{\hspace{1em}(4.2.1.3)}$$

4.2.2 蜂窝夹层结构的等效弹性模量计算

在蜂窝夹层结构的设计计算中，通常需要计算蜂窝夹层结构的等效面内拉伸模量、蜂窝夹层结构的等效剪切模量、蜂窝芯材的平拉（平压）模量和蜂窝芯材的剪切模量等主要参数。

4.2.2.1 面内拉伸弹性模量

如图所示，蜂窝夹层结构受面内拉伸载荷。

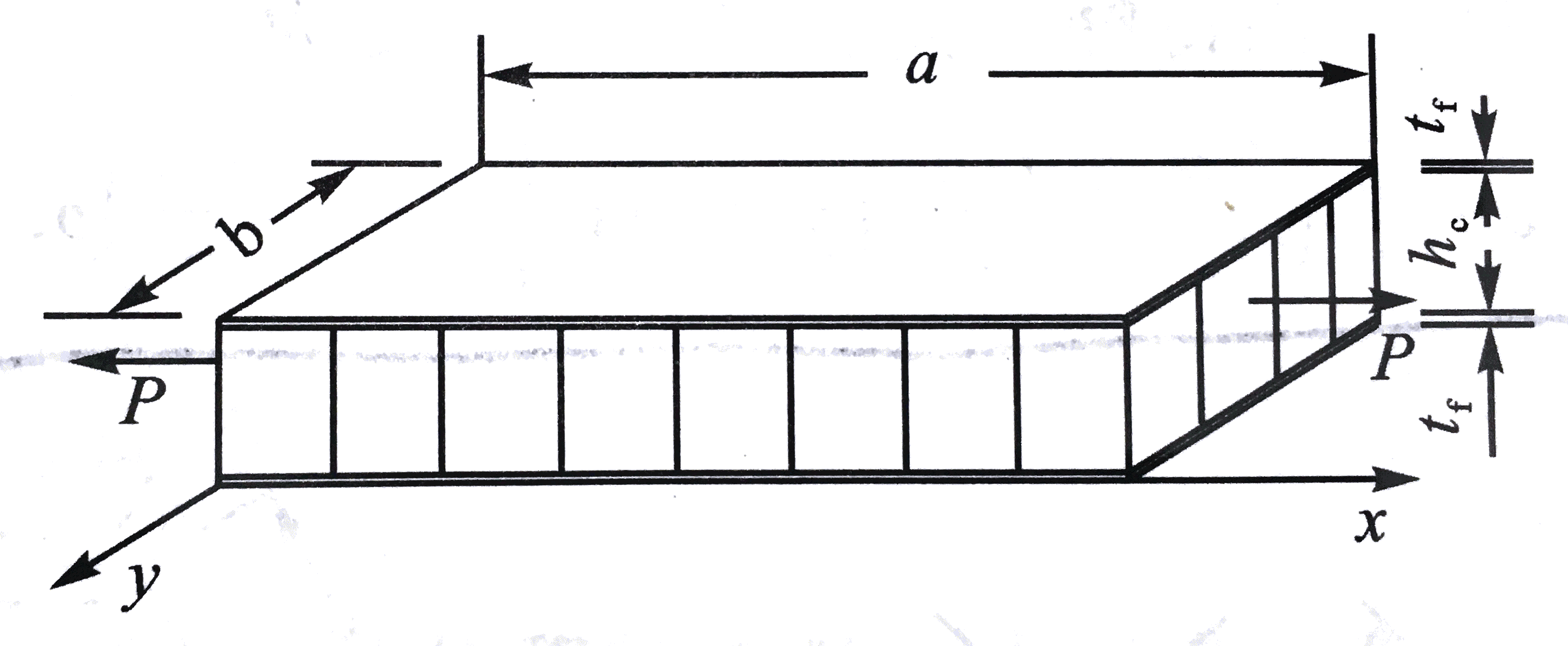
则：

$$P=2{\sigma }_f{t}_{f}b+{\sigma }_c{h}_{c}b$$

其中，${\sigma }_f$、${\sigma }_c$分别为面板和芯材的应力。若${ϵ}_x$为夹层结构的平均应变，${ϵ}_{fx}$和${ϵ}_{cx}$分别为面板和芯材的应变，$E_{fx}$和$E_{cx}$分别为面板和芯材在$x$方向的拉伸模量，则上式可写成：

$$E_x{ϵ}_{x}hb=2E_{fx}{ϵ}_{fx}{t}_{f}b+E_{cx}{ϵ}_{cx}{h}_{c}b$$

夹层结构在受拉伸是的变形协调条件为：

$${ϵ}_x={ϵ}_{fx}={ϵ}_{cx}$$

从而有：

$$E_x=E_{fx}\frac{2t_f}{h}+E_{cx}\frac{h_c}{h}$$

由于蜂窝芯材在$x$、$y$方向上的拉伸模量甚小，工程上可忽略，则：

$$E_x=E_{fx}\frac{2t_f}{h}$$

对于$x$、$y$方向正方对称的面板$E_{fx}=E_{fy}=E_f$：

$$E_x=E_y=E_f\frac{2t_f}{h}\text{\hspace{1em}(4.2.2.1.1)}$$

4.2.2.2 蜂窝夹层结构的剪切模量

如图所示，蜂窝夹层结构承受$Oxz$平面、$Oyz$平面和$Oxy$平面内的剪切，在这两种载荷作用下，夹层结构将出现不同变形。

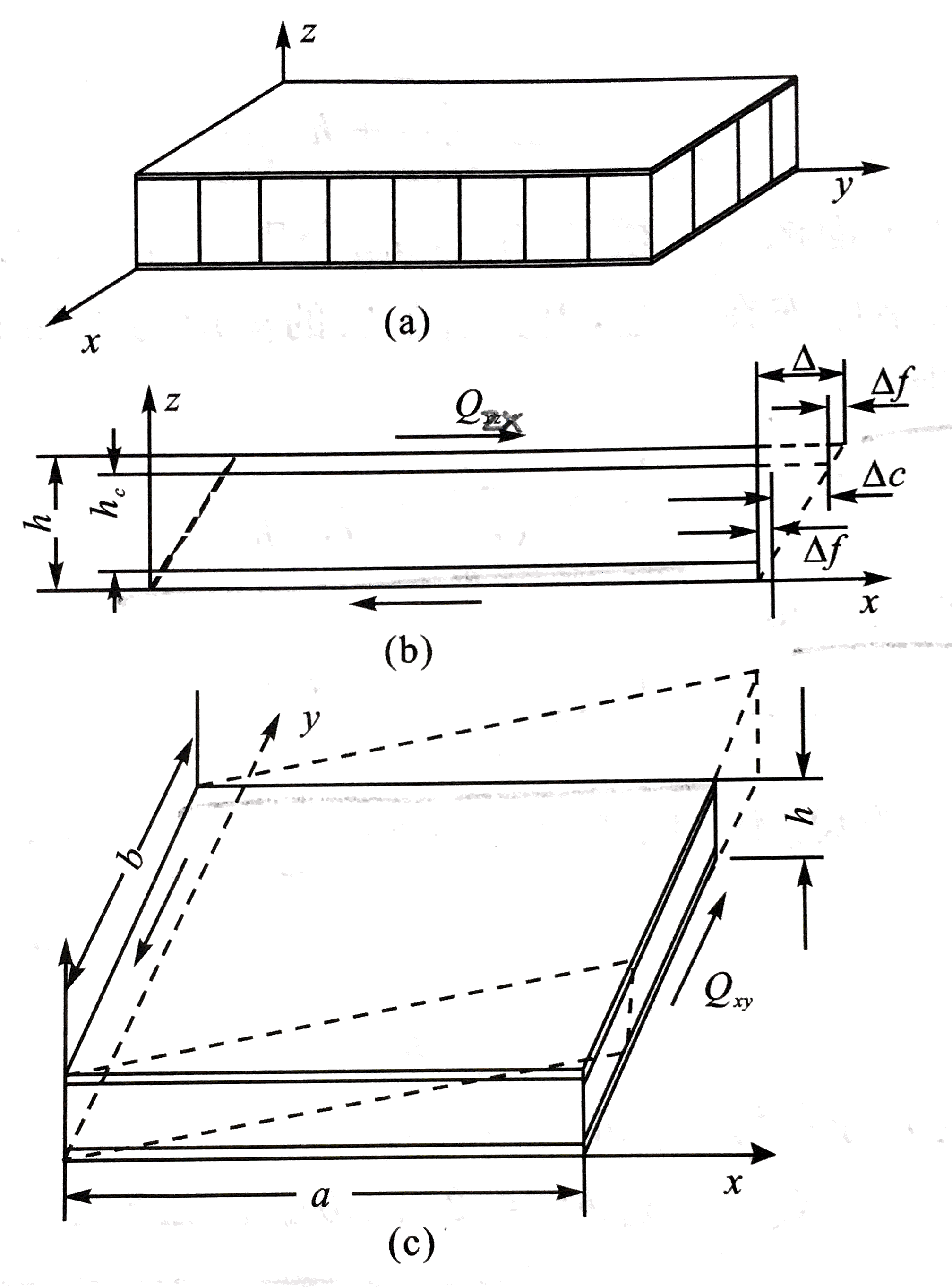
1. 蜂窝夹层在$Oxz$平面和$Oyz$平面的剪切模量
   $(b)$所示为$Oxz$平面的$Q_{xz}$载荷作用下的变形情况：

   $$\Delta =2{\Delta }_f+{\Delta }_c$$

   假定蜂窝芯材的剪应变${\gamma }_c$，面板的剪应变为${\gamma }_f$，结构的总剪应变为${\gamma }_x$，则上式可写成

   $${\gamma }_{x}h=2t_f{\gamma }_f+h_c{\gamma }_c$$

   若面板和芯材内相应的剪应力分别为${\tau }_f$和${\tau }_c$，夹层结构的相当剪应力为${\tau }_x$。夹层结构在$Oxz$面的剪切模量为$G_{xz}$，面板和芯材在$Oxz$面的剪切模量分别为$G_{fxz}$和$G_{cxz}$。则上式变成：

   $$\frac{{\tau }_x}{G_{xz}}=2t_f\frac{{\tau }_f}{G_{fxz}}+h_c\frac{{\tau }_c}{G_{cxz}}$$

   由于面板和芯材胶结在一起，${\tau }_x={\tau }_c={\tau }_f$，于是得：

   $$\frac{1}{G_{xz}}=\frac{2t_f}{G_{fxz}}+\frac{h_c}{G_{cxz}}\text{\hspace{1em}(4.2.2.2.1)}$$

   同理得$Oyz$面的剪切模量：

   $$\frac{1}{G_{yz}}=\frac{2t_f}{G_{fyz}}+\frac{h_c}{G_{cyz}}\text{\hspace{1em}(4.2.2.2.2)}$$

2. 蜂窝夹层在$Oxy$平面的剪切模量
   $(c)$所示为夹层结构在$Oxy$面内的$Q_{xy}$作用下的变形，此时整个夹层结构在$Oxy$面内的相当应力为：

   $${\tau }_{xy}=\frac{Q_{xy}}{hb}$$

   若面板和芯材的剪应力分别为${\tau }_{fxy}$和${\tau }_{cxy}$，则有：

   $$Q_{xy}={\tau }_{xy}hb=2{\tau }_{fxy}{t}_{f}b+{\tau }_{cxy}{h}_{c}b$$

   即：

   $$G_{xy}{\gamma }_{xy}h=2G_{fxy}{\gamma }_{fxy}{t}_f+G_{cxy}{\gamma }_{cxy}{h}_c$$

   由变形协调条件可知${\gamma }_{xy}={\gamma }_{fxy}={\gamma }_{cxy}$，从而得：

   $$G_{xy}=G_{fxy}\frac{2t_f}{h}+G_{cxy}\frac{h_c}{h}$$

   由于$G_{cyx}\approx 0$，所以蜂窝夹层结构$Oxy$面内的剪切模量为：

   $$G_{xy}=G_{fxy}\frac{2t_f}{h}\text{\hspace{1em}(4.2.2.2.3)}$$

4.2.2.3 蜂窝芯料的剪切模量

通常将平行于蜂窝壁重叠连接的方向定为$x$方向，称为纵向；于其垂直的方向定为$y$方向，称为横向。在计算夹层结构的剪切模量时，需知芯材的剪切模量$G_{cxz}$和$G_{cyz}$，二者往往并不相同。

1. 横向剪切模量$G_{cxz}$
   如图所示，蜂窝芯在$Oyz$面受剪时的剪流图。
   
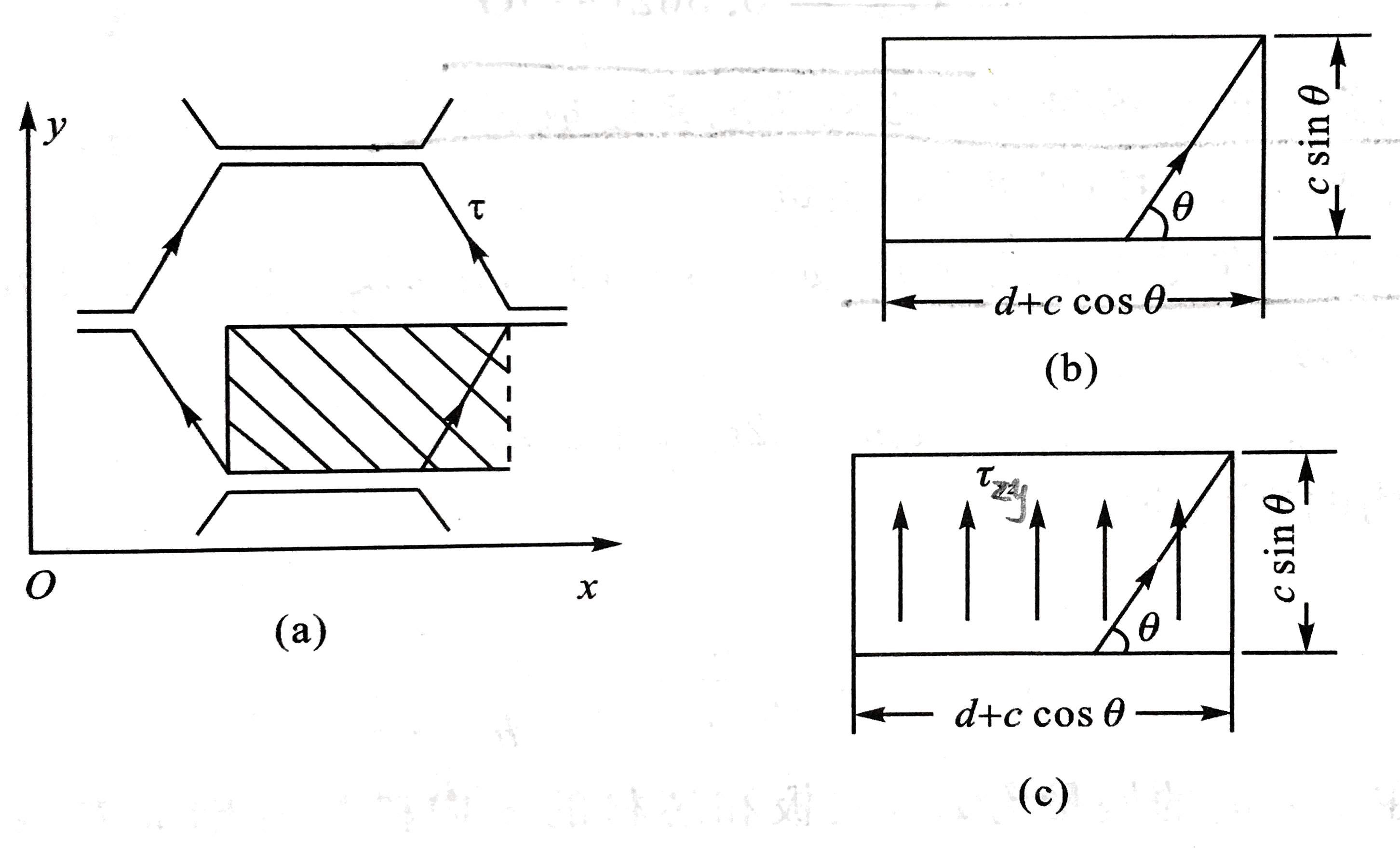
   取阴影部分为基本单元体。这个单元体内只有一个蜂窝边受剪，设这个边所受剪流为$T$。蜂窝芯材材料的剪切模量为$G_s$，厚度为$t_s$。由于$E_{cx}$很小，故$x$方向的边的拉伸应变能可略去。则此单元体的应变能为：

   $$U=\frac{(cT{)}^2{h}_c}{2G_{s}c{t}_s}=\frac{c{h}_c{T}^2}{2G_s{t}_s}$$

   将此基本单元折合为一个等体积均质实心的相当体（图中$(c)$所示）,此相当体在y方向所取单元体有相同的剪切模量。则此相当体在$y$方向所承受的剪应力为

   $${\tilde{\tau }}_{yz}=\frac{cT\sin \theta }{(d+c\cos \theta )c\sin \theta }$$

   由于为正六边形蜂窝（$d=c$、$\theta =60^{\circ }$），则：

   $${\tilde{\tau }}_{yz}=\frac{2T}{3c}$$

   此相当体的在$y$方向的剪切模量也为$G_{cxz}$，相当体的应变能为：

   $$\tilde{U}=\frac{{\tilde{\tau }}_{yz}^2}{2G_{cyz}}c\sin \theta (d+c\cos \theta )h_c=\frac{\sqrt{3}}{6}\frac{T^2{h}_c}{G_{cyz}}$$

   相当体与单元体的应变能应该相等：$U=\tilde{U}$，即：

   $$\frac{c{h}_c{T}^2}{2G_s{t}_s}=\frac{\sqrt{3}}{6}\frac{T^2{h}_c}{G_{cyz}}$$

   于是：

   $$G_{cyz}=\frac{\sqrt{3}}{3}\frac{t_s}{c}{G}_s\approx 0.58\frac{t_s}{c}{G}_s$$

   结合$(4.2.1.2)$得：

   $$G_{cyz}=0.38\frac{{\rho }_c}{{\rho }_s}{G}_s\text{\hspace{1em}(4.2.2.3.1)}$$

   上式表明蜂窝芯材的横向剪切模量与芯子的密度成正比。

2. 纵向剪切模量$G_{cyz}$
   如图所示，蜂窝芯在$Oxz$面受剪时的剪流图。
   
   同前面的分析一样。同样设蜂窝壁上的剪流为$T$，则单元体应变能为：、

   $$U=2\frac{(cT{)}^2{h}_c}{2G_{s}c{t}_s}=\frac{T^{2}c{h}_s}{G_s{t}_s}$$

   其等体积均质实心体相当体的剪应力为：

   $${\tilde{\tau }}_{xz}=\frac{cT+cT\cos \theta }{(d+c\cos \theta )c\sin \theta }=\frac{2T}{\sqrt{3}c}$$

   相当体的应变能为：

   $$\tilde{U}=\frac{{\tilde{\tau }}_{yz}^2}{2G_{cyz}}c\sin \theta (d+c\cos \theta )h_c=\frac{\sqrt{3}}{2G_{cxz}}{T}^2{h}_c$$

   二者应变能相等，$U=\tilde{U}$：

   $$\frac{T^{2}c{h}_s}{G_s{t}_s}=\frac{\sqrt{3}}{2G_{cxz}}{T}^2{h}_c$$

   于是：

   $$G_{cxz}=0.866\frac{t_s}{c}{G}_s$$

   结合$(4.2.1.2)$得：

   $$G_{cxz}=0.562\frac{{\rho }_c}{{\rho }_s}{G}_s\text{\hspace{1em}(4.2.2.3.2)}$$

   可以看出蜂窝芯的纵向剪切模量也与蜂窝芯的密度成正比。

4.2.2.4 蜂窝夹层结构的平拉（或平拉）模量

如图所示，夹层结构在$z$向受拉伸载荷$P$。

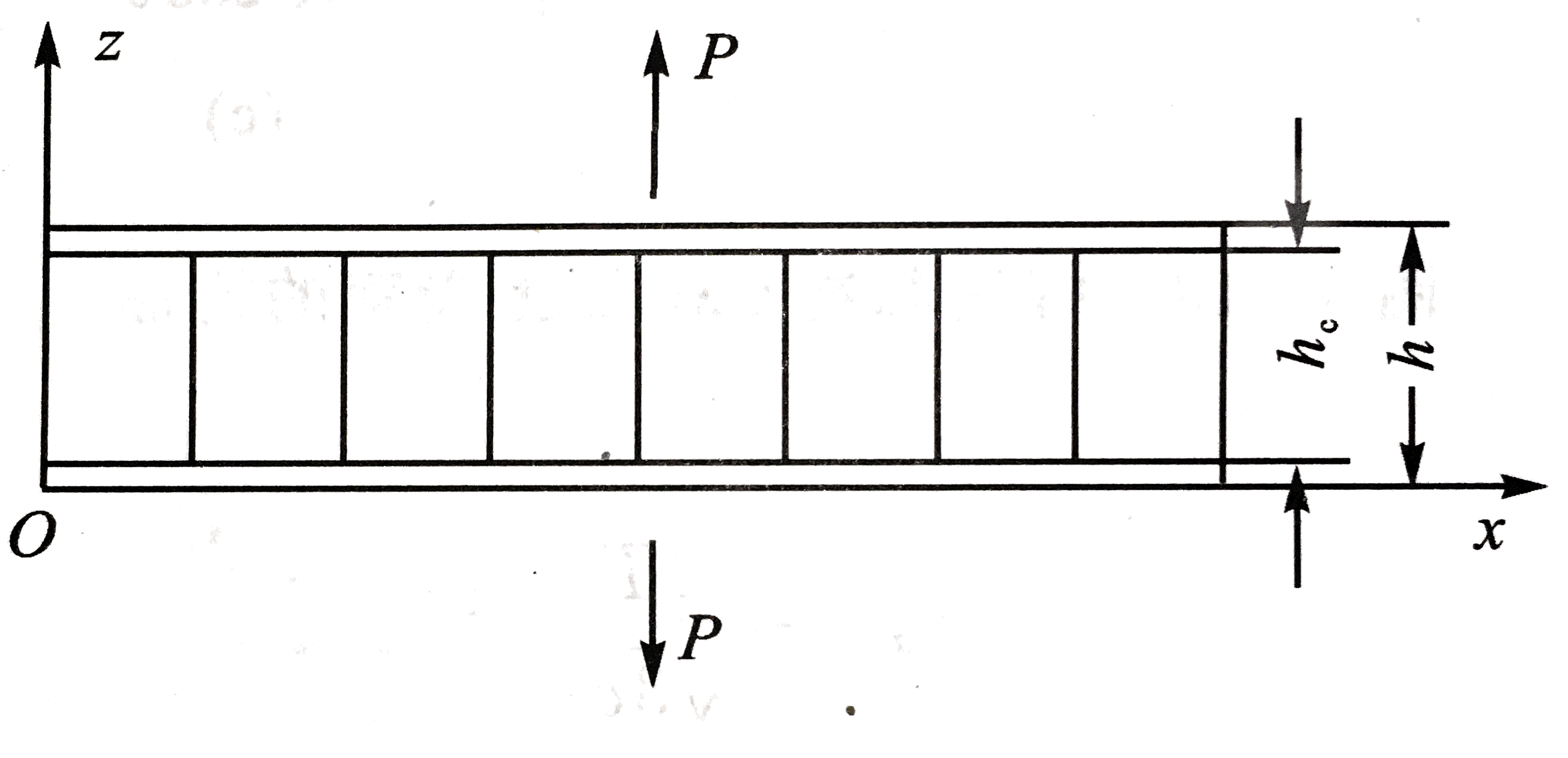
设面板和芯材分别产生应变${ϵ}_{fz}$和${ϵ}_{cz}$，夹层结构整体的应变为${ϵ}_z$。则$z$向的总变形为：

$${ϵ}_{z}h=2{ϵ}_{fz}{t}_f+{ϵ}_{cz}{h}_c$$

即：

$${ϵ}_z={ϵ}_{fz}\frac{2t_f}{h}+{ϵ}_{cz}\frac{h_c}{h}$$

夹层结构在$z$方向的模量为$E_z$，面板和芯材的$z$向模量分别为$E_{fz}$和$E_{cz}$，按上式并用胡克定律得：

$$\frac{{\sigma }_z}{E_z}=\frac{{\sigma }_{fz}}{E_{fz}}\frac{2t_f}{h}+\frac{{\sigma }_{cz}}{E_{cz}}\frac{h_c}{h}$$

由于$z$向受载，夹层结构的面板和芯材为串联，故各部分的$z$向应力相等，即${\sigma }_z={\sigma }_{fz}={\sigma }_{cz}$，所以：

$$\frac{1}{E_z}=\frac{1}{E_{fz}}\frac{2t_f}{h}+\frac{1}{E_{cz}}\frac{h_c}{h}\text{\hspace{1em}(4.2.2.4.1)}$$

其中，芯材的平拉（或平压）模量$E_{cz}$，对于六边形蜂窝芯有：

$$E_{cz}=\frac{{\rho }_c}{{\rho }_s}{E}_s\text{\hspace{1em}(4.2.2.4.2)}$$

---

本文章使用limfx的vsocde插件快速发布